Statistical Properties of Wave Chaotic Scattering and Impedance

Statistical Properties of Wave Chaotic Scattering and Impedance Matrices MURI Faculty: MURI Students: Tom Antonsen, Ed Ott, Steve Anlage, Xing Zheng, Sameer Hemmady, James Hart AFOSR-MURI Program Review

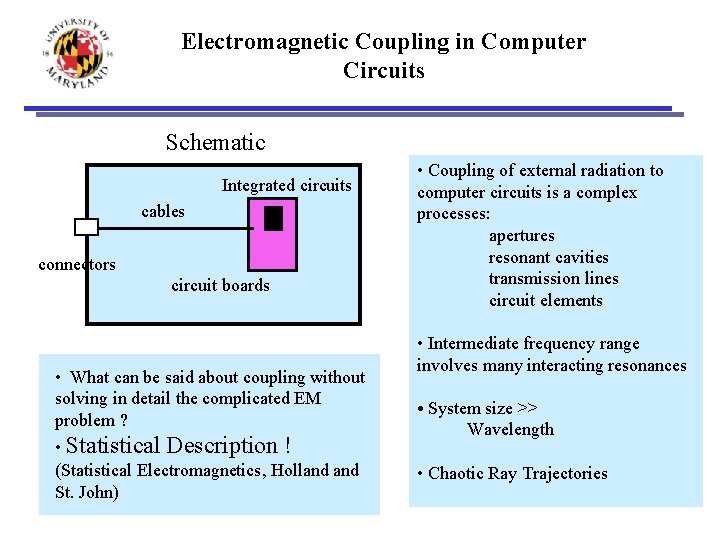
Electromagnetic Coupling in Computer Circuits Schematic Integrated circuits cables connectors circuit boards • What can be said about coupling without solving in detail the complicated EM problem ? • Statistical Description ! (Statistical Electromagnetics, Holland St. John) • Coupling of external radiation to computer circuits is a complex processes: apertures resonant cavities transmission lines circuit elements • Intermediate frequency range involves many interacting resonances • System size >> Wavelength • Chaotic Ray Trajectories

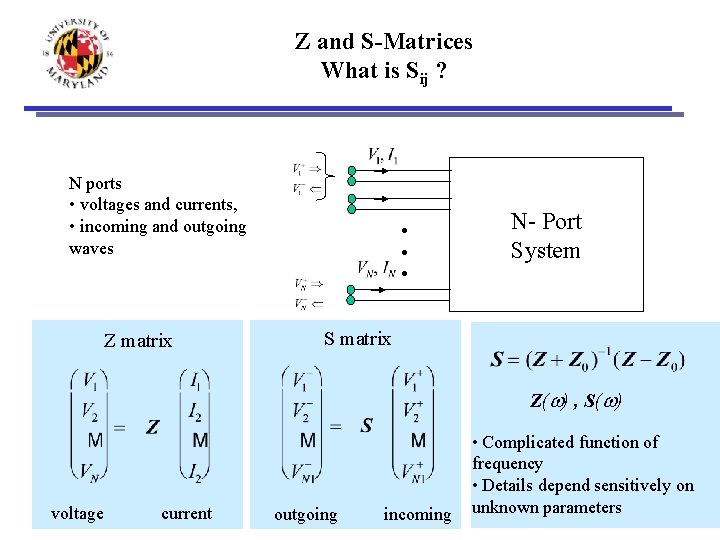
Z and S-Matrices What is Sij ? N ports • voltages and currents, • incoming and outgoing waves Z matrix • • • N- Port System S matrix Z(w) , S(w) voltage current outgoing incoming • Complicated function of frequency • Details depend sensitively on unknown parameters

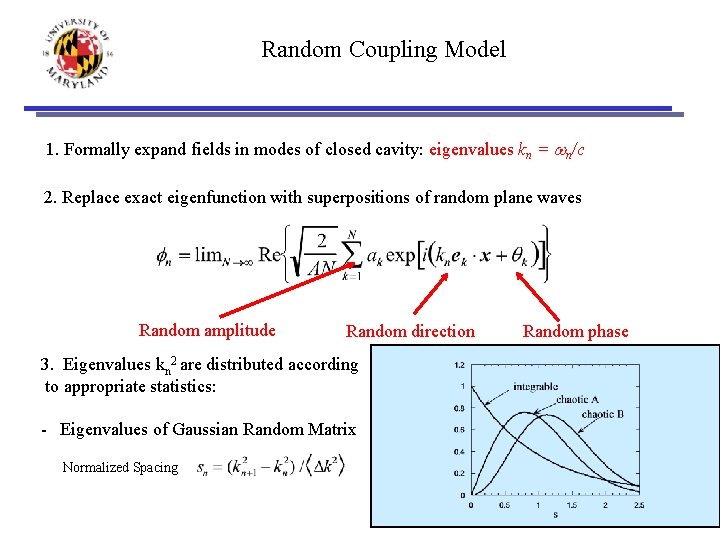
Random Coupling Model 1. Formally expand fields in modes of closed cavity: eigenvalues kn = wn/c 2. Replace exact eigenfunction with superpositions of random plane waves Random amplitude Random direction 3. Eigenvalues kn 2 are distributed according to appropriate statistics: - Eigenvalues of Gaussian Random Matrix Normalized Spacing Random phase

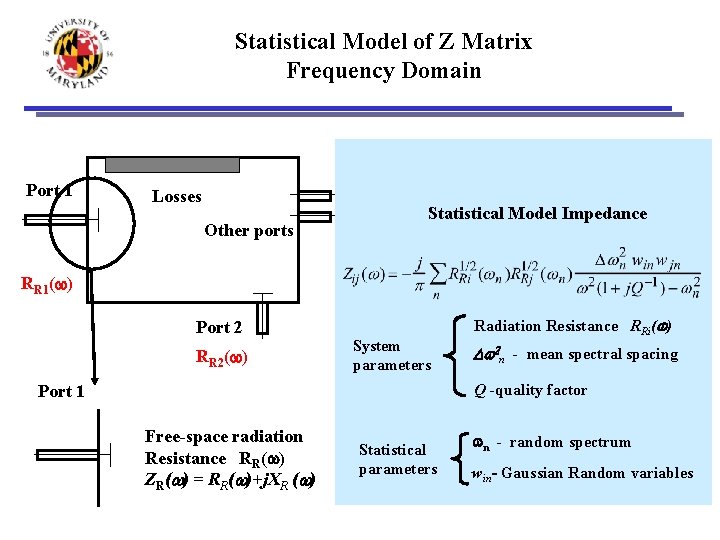
Statistical Model of Z Matrix Frequency Domain Port 1 Losses Other ports Statistical Model Impedance RR 1(w) Port 2 RR 2(w) System parameters Radiation Resistance RRi(w) Dw 2 n - mean spectral spacing Q -quality factor Port 1 Free-space radiation Resistance RR(w) ZR(w) = RR(w)+j. XR (w) Statistical parameters wn - random spectrum win- Gaussian Random variables

Model Validation Summary Single Port Case: Cavity Impedance: Radiation Impedance: Zcav = RR z + j. XR ZR = RR + j. XR Universal normalized random impedance: z = r + jx Statistics of z depend only on damping parameter: (Q-width/frequency spacing) Validation: HFSS simulations Experiment (Hemmady and Anlage) k 2/(QDk 2)

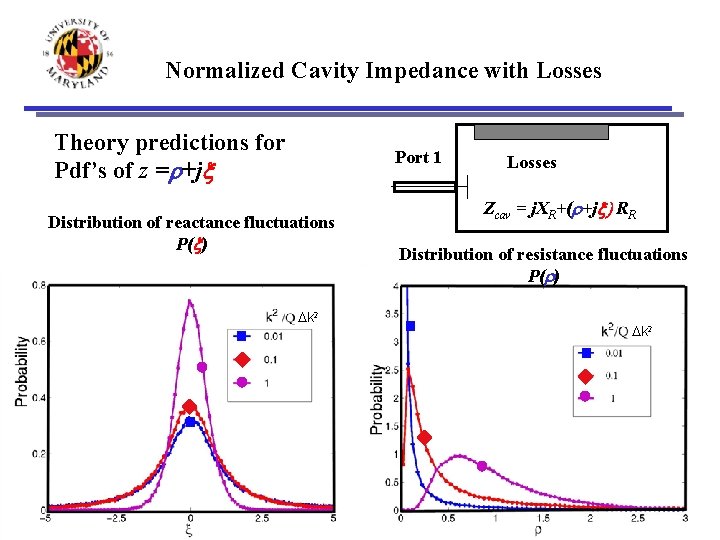
Normalized Cavity Impedance with Losses Theory predictions for Pdf’s of z =r+jx Port 1 Distribution of reactance fluctuations P(x) Dk 2 Losses Zcav = j. XR+(r+jx) RR Distribution of resistance fluctuations P(r) Dk 2

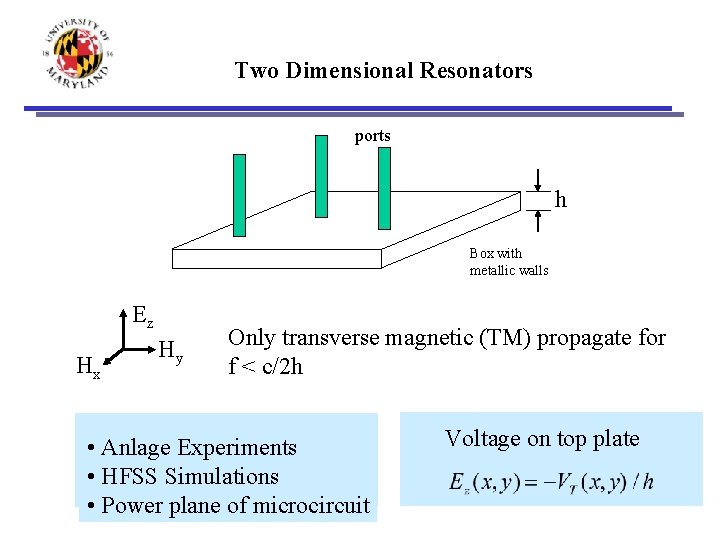
Two Dimensional Resonators ports h Box with metallic walls Ez Hx Hy Only transverse magnetic (TM) propagate for f < c/2 h • Anlage Experiments • HFSS Simulations • Power plane of microcircuit Voltage on top plate

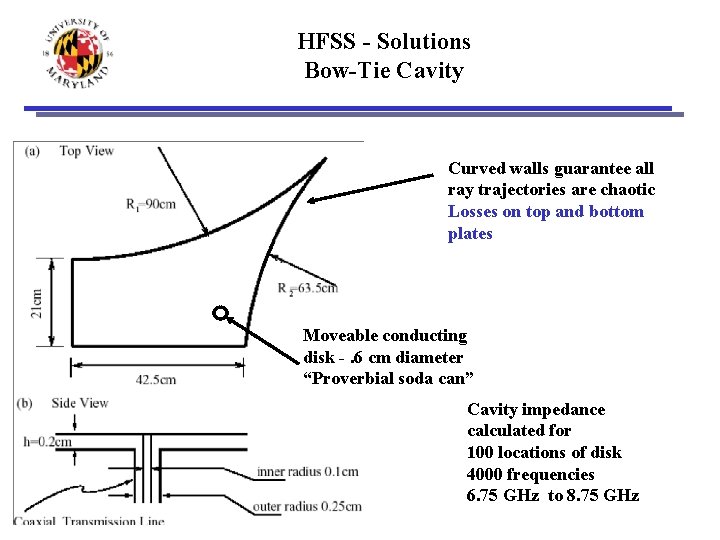
HFSS - Solutions Bow-Tie Cavity Curved walls guarantee all ray trajectories are chaotic Losses on top and bottom plates Moveable conducting disk -. 6 cm diameter “Proverbial soda can” Cavity impedance calculated for 100 locations of disk 4000 frequencies 6. 75 GHz to 8. 75 GHz

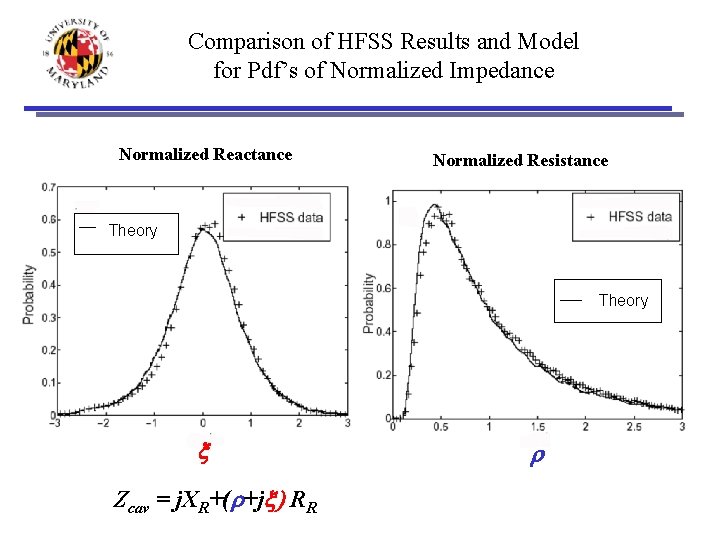
Comparison of HFSS Results and Model for Pdf’s of Normalized Impedance Normalized Reactance Normalized Resistance Theory x Zcav = j. XR+(r+jx) RR r

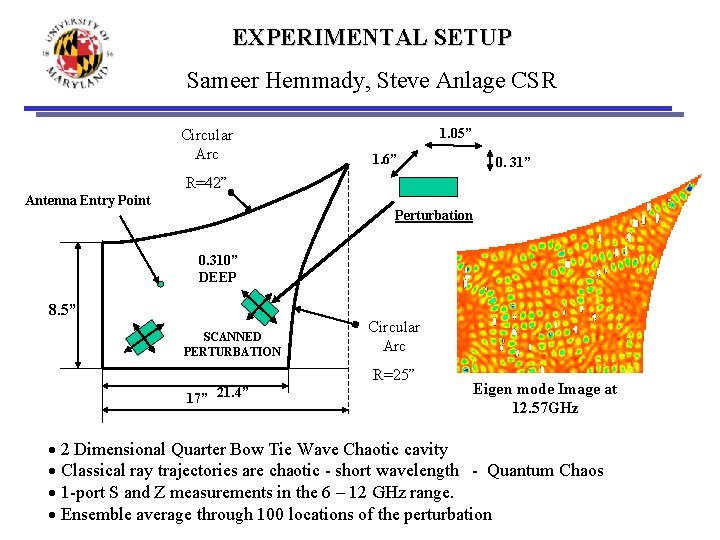
EXPERIMENTAL SETUP Sameer Hemmady, Steve Anlage CSR Circular Arc 1. 05” 1. 6” 0. 31” R=42” Antenna Entry Point Perturbation 0. 310” DEEP 8. 5” SCANNED PERTURBATION Circular Arc R=25” 17” 21. 4” Eigen mode Image at 12. 57 GHz 2 Dimensional Quarter Bow Tie Wave Chaotic cavity Classical ray trajectories are chaotic - short wavelength - Quantum Chaos 1 -port S and Z measurements in the 6 – 12 GHz range. Ensemble average through 100 locations of the perturbation

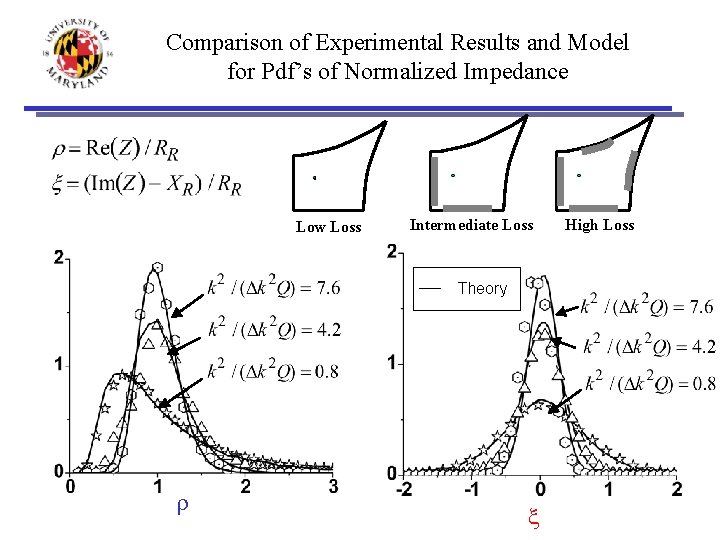
Comparison of Experimental Results and Model for Pdf’s of Normalized Impedance Low Loss Intermediate Loss Theory r x High Loss

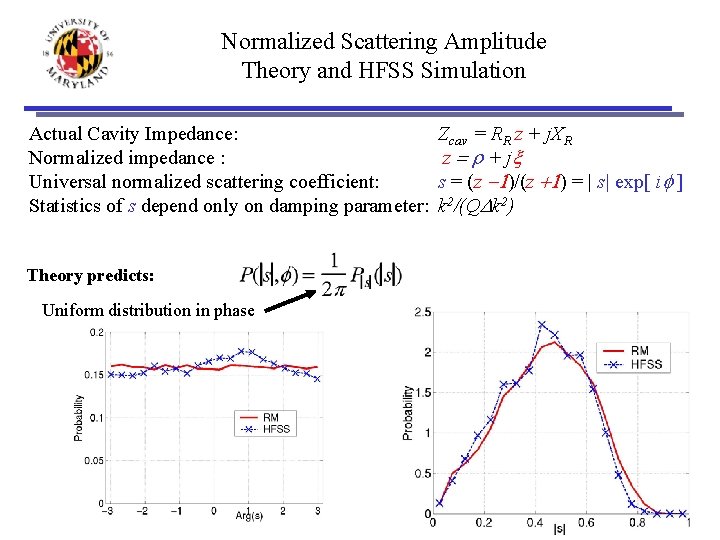
Normalized Scattering Amplitude Theory and HFSS Simulation Actual Cavity Impedance: Normalized impedance : Universal normalized scattering coefficient: Statistics of s depend only on damping parameter: Theory predicts: Uniform distribution in phase Zcav = RR z + j. XR z = r + jx s = (z -1)/(z +1) = | s| exp[ if ] k 2/(QDk 2)

Experimental Distribution of Normalized Scattering Coefficient s=|s|exp[if] 1 5 p/8 ln [P(|s|2)] Distribution of Reflection Coefficient 3 p/8 a) Theory 7 p/8 0 - p/8 11 - 3 p/8 0 1 Distribution independent of f |s|2

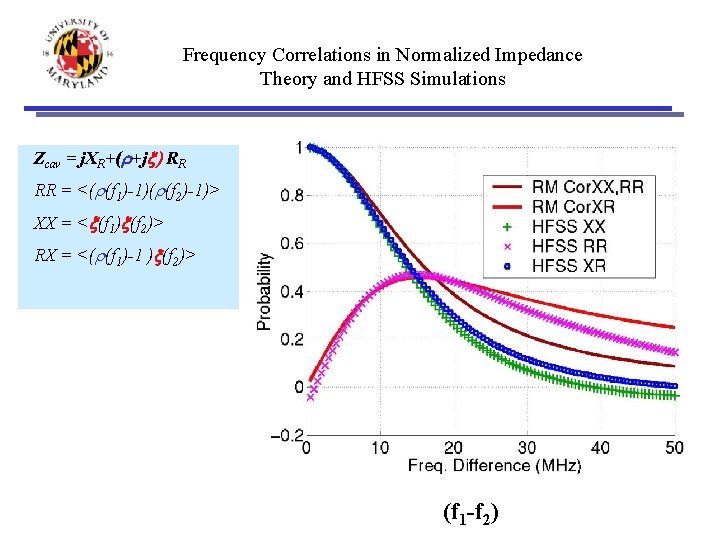
Frequency Correlations in Normalized Impedance Theory and HFSS Simulations Zcav = j. XR+(r+jx) RR RR = <(r(f 1)-1)(r(f 2)-1)> XX = <x(f 1)x(f 2)> RX = <(r(f 1)-1 )x(f 2)> (f 1 -f 2)

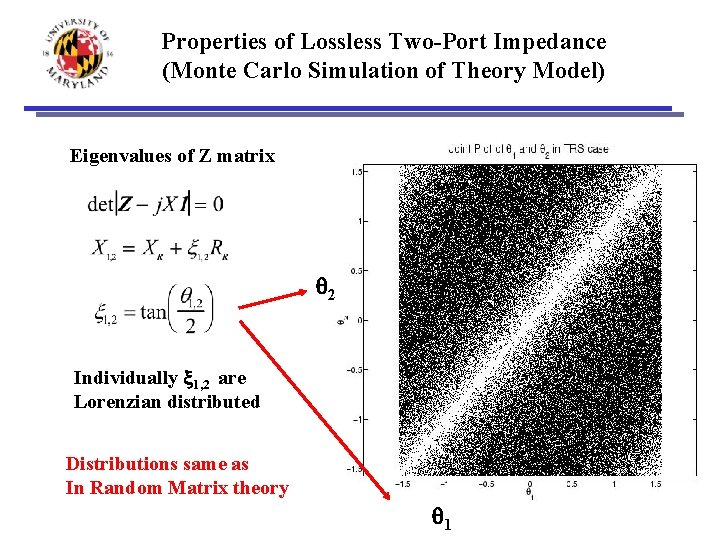
Properties of Lossless Two-Port Impedance (Monte Carlo Simulation of Theory Model) Eigenvalues of Z matrix q 2 Individually x 1, 2 are Lorenzian distributed Distributions same as In Random Matrix theory q 1

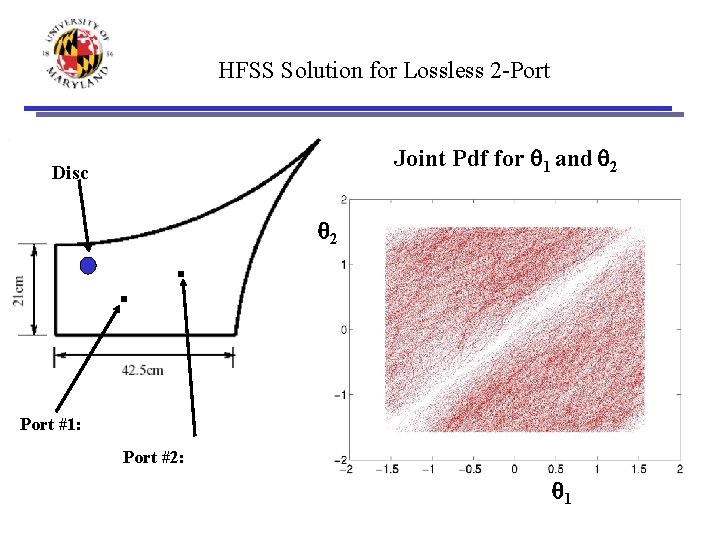
HFSS Solution for Lossless 2 -Port Joint Pdf for q 1 and q 2 Disc q 2 Port #1: Port #2: q 1

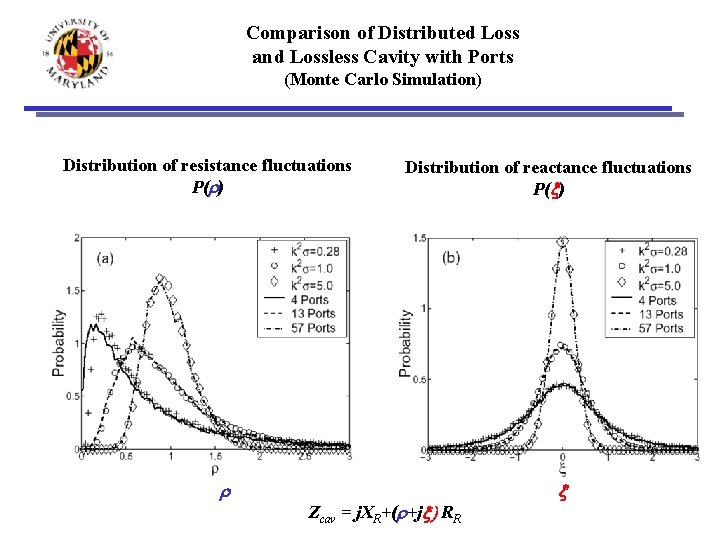
Comparison of Distributed Loss and Lossless Cavity with Ports (Monte Carlo Simulation) Distribution of resistance fluctuations P(r) r Distribution of reactance fluctuations P(x) Zcav = j. XR+(r+jx) RR x

Time Domain Model for Impedance Matrix Frequency Domain wn- Gaussian Random variables Statistical Parameters Time Domain wn - random spectrum wn- Gaussian Random variables

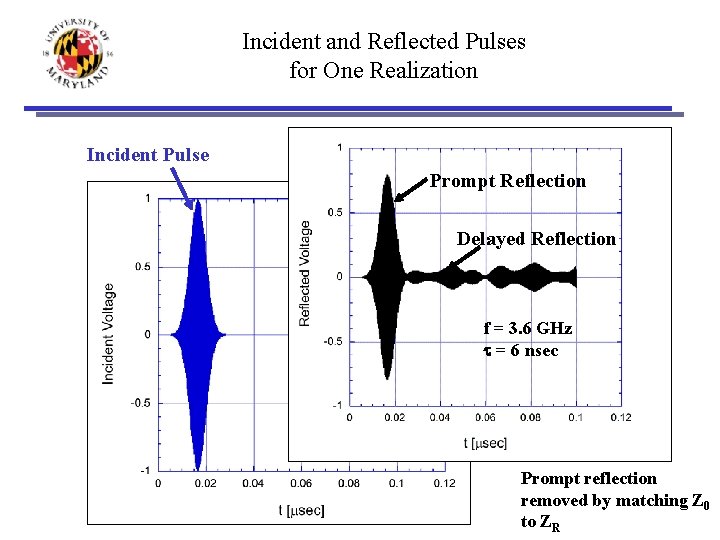
Incident and Reflected Pulses for One Realization Incident Pulse Prompt Reflection Delayed Reflection f = 3. 6 GHz t = 6 nsec Prompt reflection removed by matching Z 0 to ZR

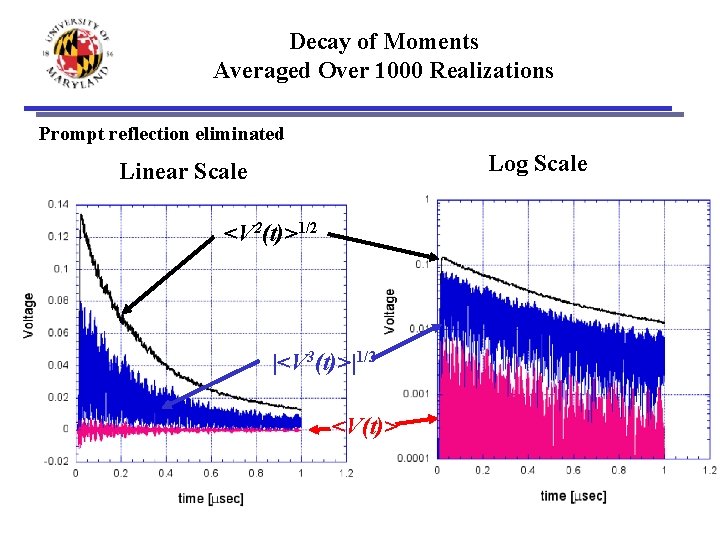
Decay of Moments Averaged Over 1000 Realizations Prompt reflection eliminated Log Scale Linear Scale <V 2(t)>1/2 |<V 3(t)>|1/3 <V(t)>

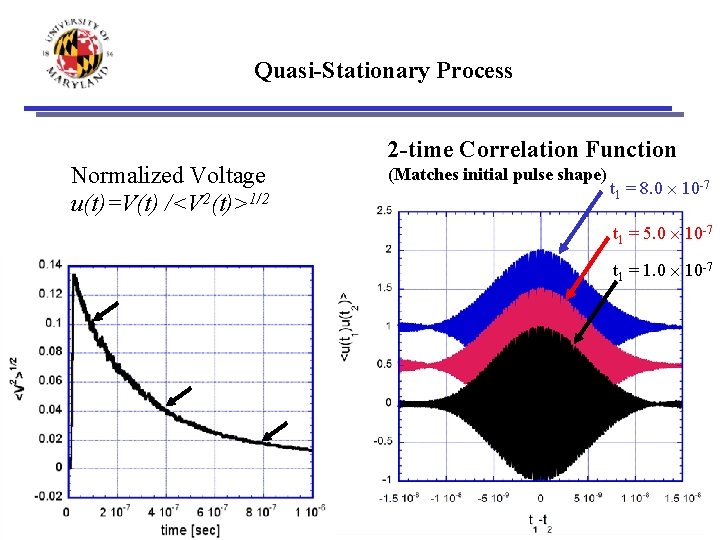
Quasi-Stationary Process Normalized Voltage u(t)=V(t) /<V 2(t)>1/2 2 -time Correlation Function (Matches initial pulse shape) t 1 = 8. 0 10 -7 t 1 = 5. 0 10 -7 t 1 = 1. 0 10 -7

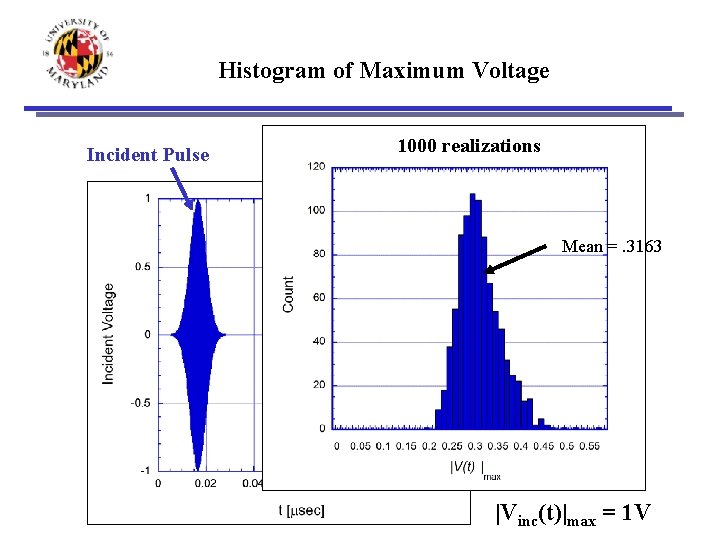
Histogram of Maximum Voltage Incident Pulse 1000 realizations Mean =. 3163 |Vinc(t)|max = 1 V

Progress • Direct comparison of random coupling model with -random matrix theory P -HFSS solutions P -Experiment P • Exploration of increasing number of coupling ports P • Study losses in HFSS P • Time Domain analysis of Pulsed Signals -Pulse duration -Shape (chirp? ) Current • Generalize to systems consisting of circuits and fields Future

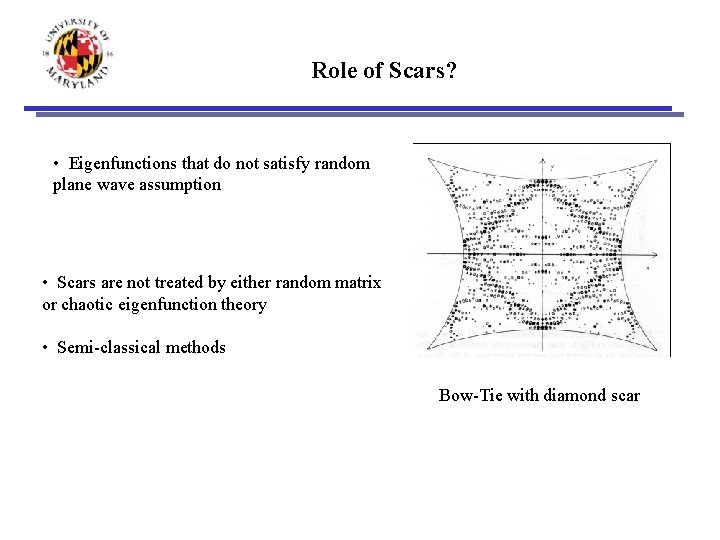
Role of Scars? • Eigenfunctions that do not satisfy random plane wave assumption • Scars are not treated by either random matrix or chaotic eigenfunction theory • Semi-classical methods Bow-Tie with diamond scar

Future Directions • Can be addressed -theoretically -numerically -experimentally Features: Ray splitting Losses Additional complications to be added later HFSS simulation courtesy J. Rodgers