STATISTICA a a 2003 2004 LA STATISTICA INFERENZIALE

STATISTICA a. a. 2003 -2004 – LA STATISTICA INFERENZIALE – TEST A UNA CODA E A DUE CODE – TEST DEL CHI QUADRATO

CONFRONTO FRA POPOLAZIONI – Uno scopo della statistica è determinare se le caratteristiche di due popolazioni sono differenti o meno. – Si traggono cioè conclusioni sulla popolazione, determinando un’inferenza statistica. – Possiamo confrontare campioni o popolazioni attraverso le medie o le varianze.

CONFRONTO FRA POPOLAZIONI – Per effettuare un confronto si ricorre al test statistico. – Il test statistico è il procedimento che consente di rifiutare o non rifiutare (accettare ) un’ipotesi sulla popolazione – Il test assegna un certo valore di probabilità all’ipotesi che viene formulata.

L’IPOTESI NULLA – Si usa in genere la cosiddetta ipotesi nulla (H 0). – Essa postula come inesistenti (nulle, pari a zero) le differenze fra le caratteristiche delle popolazioni in esame (H 0 : A=B). – Un test statistico consente di provare l’inaccettabilità (con una certa quota di errore) di un’ipotesi, ma non di provarla.

L’IPOTESI NULLA – Se la probabilità che l’ipotesi nulla sia vera è bassa, vorrà dire che le popolazioni confrontate sono verosimilmente differenti. – Confrontare un modello con un campione sperimentale, tramite un test statistico, significa provare la concordanza tra i dati reali e il modello, cioè la validità del modello.

L’IPOTESI NULLA – Prima dell’esperimento si stabilisce il valore limite per la probabilità che l’ipotesi nulla sia vera. – Per probabilità inferiori a tale valore stimeremo falsa l’ipotesi nulla. – Per probabilità superiori, non si è in grado di rifiutare l’ipotesi nulla.

L’IPOTESI NULLA – Per convenzione si adottano due livelli di significatività: • se la probabilità che l’ipotesi nulla sia vera è uguale o minore al 5% (p<=0. 05) si dice che la differenza fra le popolazioni considerate è significativa • se la probabilità è minore o uguale all’ 1% (p<=0. 01) si dice che la differenza fra le popolazioni è altamente significativa.

L’IPOTESI NULLA • Se la probabilità è maggiore di 0. 05, non si può concludere che le popolazioni considerate sono uguali, ma si può ammettere di non avere elementi sufficienti per affermare l’esistenza di una differenza. • Il livello di significatività è il rischio di rifiutare erroneamente l’ipotesi nulla quando questa è vera.

L’IPOTESI NULLA • Questo errore è definito come errore di I tipo o errore a. • La probabilità di non rifiutare l’ipotesi nulla quando questa è in realtà falsa (ossia di accettare un’ipotesi nulla falsa) viene detta errore di II tipo o errore b.

STRUTTURA DEI TEST – Un test di significatività consiste nel calcolo di un parametro e della distribuzione di probabilità ad esso associata. – Questi parametri (chi quadrato, t di student, ecc. ) hanno distribuzioni di probabilità diverse a seconda del numero di gradi di libertà (Gd. L) impiegati nel calcolo. – Queste diverse distribuzioni sono tabulate su apposite tavole.

USO DELLE TAVOLE – Le tavole permettono di evitare di ricorrere alle equazioni delle curve di distribuzione del parametro. – In una tavola vengono riportati i valori del parametro che vengono superati nel 5% dei casi, o nell’ 1% o in una frazione interessante (10%, 50%, ecc. ). – Ottenuto il valore del parametro si valuta sulla tavola se supera il valore corrispondente alla probabilità prescelta.

USO DELLE TAVOLE – Nel caso in cui il parametro superi tale valore critico, la probabilità che ciò sia avvenuto casualmente è inferiore alla probabilità critica prescelta. – Quindi si considerano significativamente differenti le due popolazioni in questione. – In tal modo la probabilità di definire differenti popolazioni che non lo sono (errore del I tipo) è pari al livello critico prescelto (es. 5%).

TEST A UNA CODA E TEST A DUE CODE – Supponiamo di confrontare due serie di dati A e B – Se in seguito ad un test statistico rifiutiamo l’ipotesi nulla H 0 : A=B dobbiamo assumere un’ipotesi alternativa. – Si possono creare due diverse situazioni: • può interessare solo la differenza fra le due serie di dati nel senso di A>B (oppure A <B) e quindi l’ipotesi alternativa sarà H 1 : A>B

TEST A UNA CODA E TEST A DUE CODE – Supponiamo di confrontare due serie di dati A e B – Se in seguito ad un test statistico rifiutiamo l’ipotesi nulla H 0 : A=B dobbiamo assumere un’ipotesi alternativa. – Si possono creare due diverse situazioni: • può interessare solo la differenza fra le due serie di dati nel senso di A>B (oppure A <B) e quindi l’ipotesi alternativa sarà H 1 : A>B oppure H 1 : B>A

TEST A UNA CODA E TEST A DUE CODE • Può non interessare la deviazione in un solo senso e quindi ci si limita alla verifica dell’ipotesi di uguaglianza fra A e B. • Nel primo caso (test a una coda o unilaterale) si deve considerare la probabilità che la serie A sia maggiore della serie B • Nel secondo caso (test a due code o bilaterale) si deve considerare la probabilità che la serie A sia maggiore della B oppure che la B sia maggiore della A.

TEST A UNA CODA E TEST A DUE CODE • Se p 1=P(A>B) e p 2=P(B>A), nel caso del test a due code si avrà p. T=p 1+p 2=Probabilità totale • Nella distribuzione normale, se si ha una probabilità del 5% di trovare un valore esterno a m +/- 1. 96 s (probabilità a due code), si ha una probabilità del 2. 5% di trovare un valore superiore a m +1. 96 s (probabilità ad una coda).

TEST A UNA CODA E A DUE CODE – All’inizio dell’esperimento occorre stabilire se il test di significatività sarà a una o a due code, ossia se interessano le variazioni in un solo senso (maggiore o minore) o in tutti e due i sensi. – Un certo valore del parametro sarà significativo a livello di probabilità p per il test bilaterale, al livello p/2 per il test unilaterale.

TEST A UNA CODA E A DUE CODE – La scelta del test unilaterale non dovrebbe essere presa dopo aver visto i dati e la direzione della loro deviazione, ma a priori e solo se si ha la certezza che le deviazioni in una direzione si verificano solo per caso e quindi non saranno mai significative. Ciò avviene raramente: è meglio usare i test bilaterali anche se hanno livello critico più alto e quindi significatività minore.

TEST DEL CHI-QUADRATO – Supponiamo di avere due popolazioni nelle quali ogni individuo abbia probabilità P 1 e P 2 di mostrare la caratteristica A. – In un campione casuale proveniente dalla prima popolazione, r membri hanno la caratteristica A e quindi frequenza relativa r 1/n 1 – Nella seconda popolazione la frequenza relativa è r 2/n 2.

TEST DEL CHI-QUADRATO – Questi dati possono essere esposti nella tabella di contingenza 2 x 2: Caratteristica A Presente Assente campione 1 r 1 n 1 -r 1 n 1 campione 2 r 2 n 2 -r 2 n 2 __________________ r 1+r 2 (n 1 -r 1)+(n 2 -r 2) n 1+n 2

TEST DEL CHI-QUADRATO – Il totale delle osservazioni è a destra in basso. – Le quatto celle interne rappresentano le frequenze osservate. – L’ipotesi nulla afferma che la frequenza relativa della caratteristica A è uguale nelle due popolazioni (P 1=P 2).

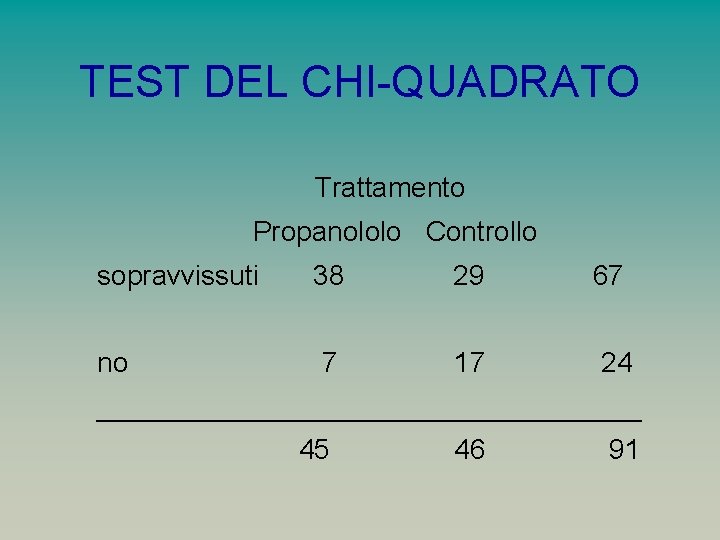
TEST DEL CHI-QUADRATO – Ad esempio abbiamo due campioni indipendenti di 45 e 46 pazienti affetti da infarto acuto. – Nel primo gruppo viene somministrato propanololo, nel secondo no. – Ad un mese di distanza si valutano sopravvissuti e si ottiene la seguente tabella:

TEST DEL CHI-QUADRATO Trattamento Propanololo Controllo sopravvissuti no 38 29 7 17 67 24 __________________ 45 46 91

TEST DEL CHI-QUADRATO – Secondo l’ipotesi nulla i tassi di sopravvissuti nelle due popolazioni sono identici. Tale tasso, stimato sui campioni, si ottiene dal rapporto 67/91 = 0. 736. – Se è vera l’ipotesi nulla, la proporzione di sopravvissuti deve essere mantenuta nei due gruppi (numero di unità attese). – Nel primo gruppo il numero atteso di sopravvissuti è 45(67/91)=33. 132

TEST DEL CHI-QUADRATO – Nel gruppo di controllo il numero atteso è 46(67/91)=33. 868. – Allo stesso modo il numero atteso di decessi è nel primo gruppo 45(24/91)= 11. 868 e nel gruppo di controllo 46(24/91)=12. 132

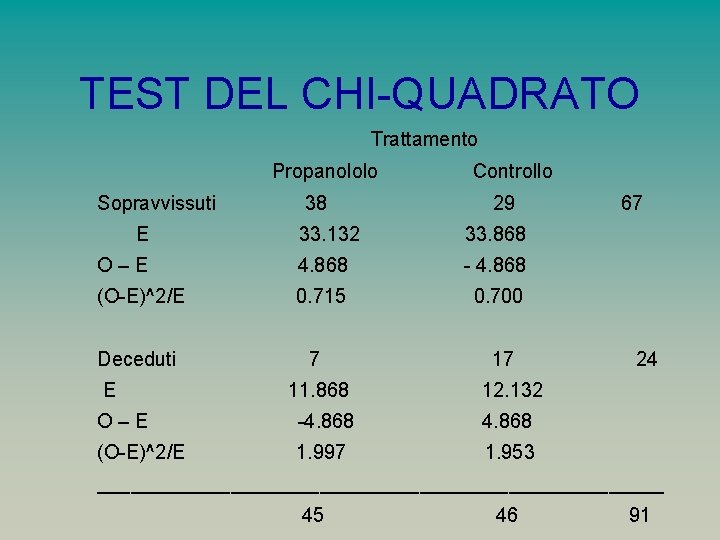
TEST DEL CHI-QUADRATO – Il test del chiquadrato per il confronto di due proporzioni in campioni indipendenti si basa sulla differenza frequenze osservate O e attese E:

TEST DEL CHI-QUADRATO Trattamento Propanololo Sopravvissuti E 38 Controllo 29 33. 132 33. 868 O–E 4. 868 - 4. 868 (O-E)^2/E 0. 715 0. 700 Deceduti E 7 11. 868 17 67 24 12. 132 O–E -4. 868 (O-E)^2/E 1. 997 1. 953 __________________________ 45 46 91

TEST DEL CHI-QUADRATO – I valori di E danno come somma di riga e di colonna i totali osservati, ed è per questo che i quattro scarti hanno lo stesso valore assoluto. – Tanto maggiore è lo scarto tanto più è ragionevole orientarsi contro l’ipotesi zero. – E’ ragionevole dividere il quadrato degli scarti per i valori attesi, in modo che la differenza venga “normalizzata”.

TEST DEL CHI-QUADRATO – Calcolato il valore atteso di una cella, visto che gli E danno gli stessi totali di riga e di colonna, le altre quantità attese si possono derivare per sottrazione dai totali marginali: esiste quindi una sola quantità attesa indipendente e per questo si dice che per una tabella di contingenza 2 x 2 vi è un grado di libertà (Gd. L) per il calcolo del chi-quadrato. – Il calcolo del chi-quadrato è la sommatoria delle quattro celle (O-E)^2/E: – Χ 2= 0. 715 + 0. 7 + 1. 997 + 1. 953 = 5. 365

TEST DEL CHI-QUADRATO – Nella tabella per la distribuzione chi-quadrato con 1 Gd. L si nota che il valore calcolato è compreso fra i valori 5. 02 e 6. 63, corrispondenti a p=0. 025 e p=0. 01. – Quindi la differenza fra le due mortalità è significativa perchè p<0. 05. – La stessa procedura di calcolo si può estendere a tabelle 2 * k o addirittura r * k per confrontare più campioni. – I Gd. L di una tabella r * k saranno (r-1) * (k-1).

TEST DEL CHI-QUADRATO – Esiste un modo alternativo di calcolo per il chiquadrato: Colonne a b r 1 c d r 2 Righe _______________________ c 1 c 2 N

CORREZIONE DI YATES – Va ricordato che il test chi-quadrato va usato con tabelle le cui entrate siano frequenze. E’ un errore usarlo con valori medi oppure percentuali. – Il test chi-quadrato è un metodo approssimato valido quando le frequenze sono grandi. – Una regola perchè sia valido è che il valore atteso di ogni cella sia maggiore o uguale a 5. – Quando le frequenze attese sono basse (ma sempre >5) si applica la correzione di Yates che riduce di ½ la grandezza assoluta di (O-E) per ciascuna cella:

CORREZIONE DI YATES

CORREZIONE DI YATES – La correzione è dovuta al fatto che il chi-quadrato si basa sull’approssimazione normale della binomiale e quindi si tratta di una correzione per la continuità. – Nel nostro esempio utilizzando le nuove formule si ottiene ancora una p significativa, anche se meno significativa che nel caso senza correzione.

TEST ESATTO DI FISHER • Per frequenze assolute molto basse anche la correzione per la continuità non è sufficiente. • Quando la numerosità totale è inferiore a 20 o è compresa fra 20 e 40 ma il valore atteso più basso è inferiore a 5 si usa il test esatto di Fisher. • Supponiamo di dover confrontare la virulenza di due ceppi batterici A e B dopo inoculazione in cavie:

TEST ESATTO DI FISHER Ceppo batteri Viva A B 6 4 14 12 10 Esito cavie Morta 26 ____________________ 20 16 36

TEST ESATTO DI FISHER • Il campione non è grande e le frequenze attese delle due prime celle sono basse. • L’ipotesi nulla ci dice che la proporzione dei morti nei due gruppi di animali è la stessa. • In pratica si calcola la probabilità totale del campione osservato secondo la formula di Fisher ( r 1! r 2 ! c 1 ! c 2 !)/ (a! b! c! d! N!) e poi si va a vedere nella tabella corrispondente alla distribuzione risultante della probabilità cumulativa.