Speed the distance covered per unit of time

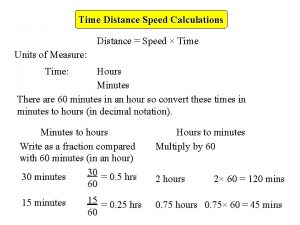
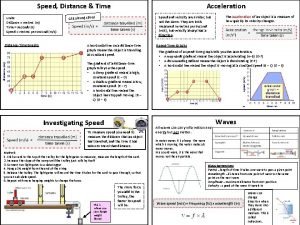
Speed: the distance covered per unit of time. A measure of how fast something is moving. • the rate at which distance is covered. Ex: 100 km/hr, 55 mph, 30 m/s Equation: S=d/t s = speed d = distance (m, km, cm, mi, ft) t = time (s, hr, day, minute, year, millennium )

Velocity When we say that a car travels 60 km/hr, we are indicating it’s speed. When we say that a car is traveling 60 km/hr to the north, we are indicating it’s velocity. Velocity: speed in a given direction • Ex: 100 km/hr East, 55 mph North, 30 m/s Southwest • Equation: v = d / t Speed is a description of how fast an object moves; velocity is how fast it moves AND in what direction.

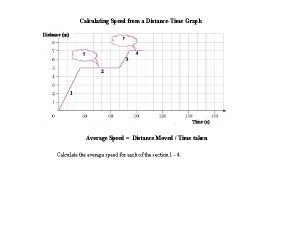
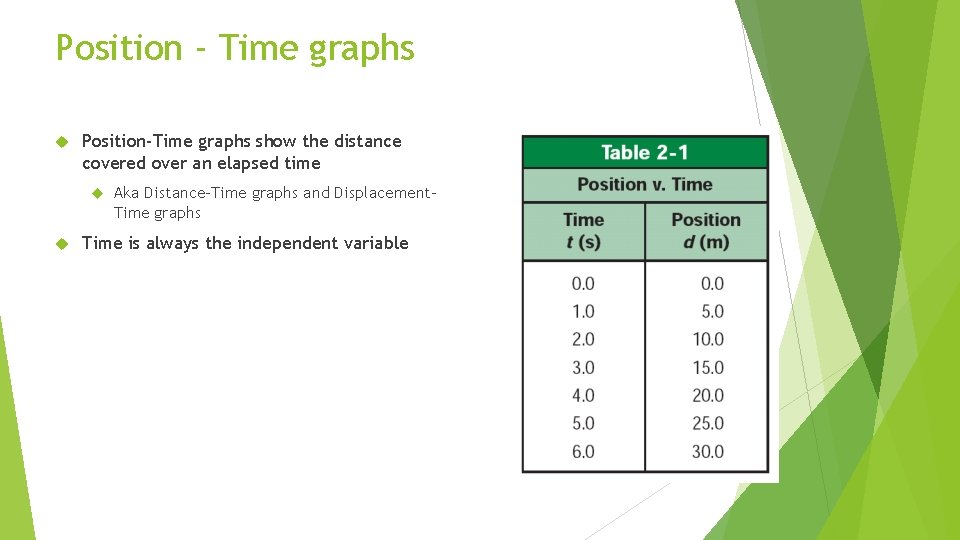
Position - Time graphs Position-Time graphs show the distance covered over an elapsed time Aka Distance-Time graphs and Displacement. Time graphs Time is always the independent variable

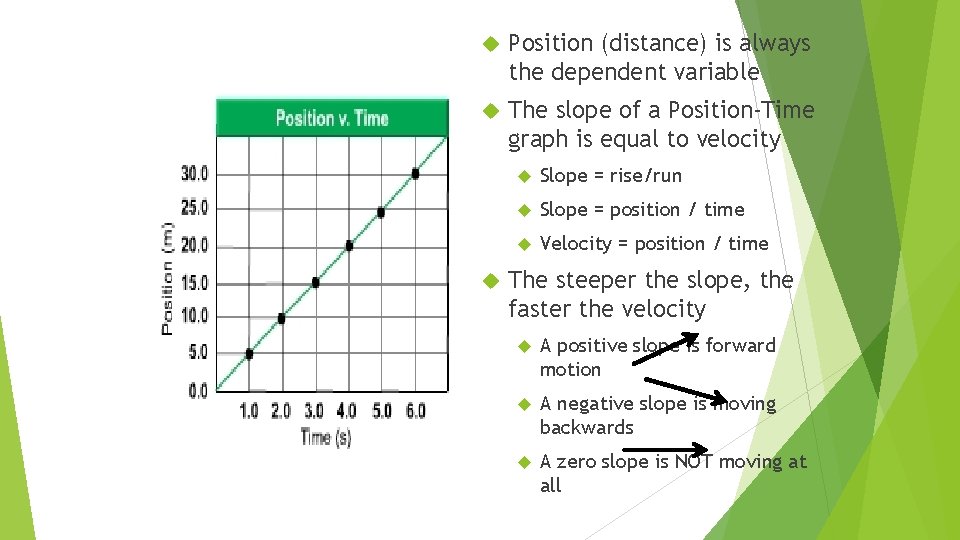
Position (distance) is always the dependent variable The slope of a Position-Time graph is equal to velocity Slope = rise/run Slope = position / time Velocity = position / time The steeper the slope, the faster the velocity A positive slope is forward motion A negative slope is moving backwards A zero slope is NOT moving at all

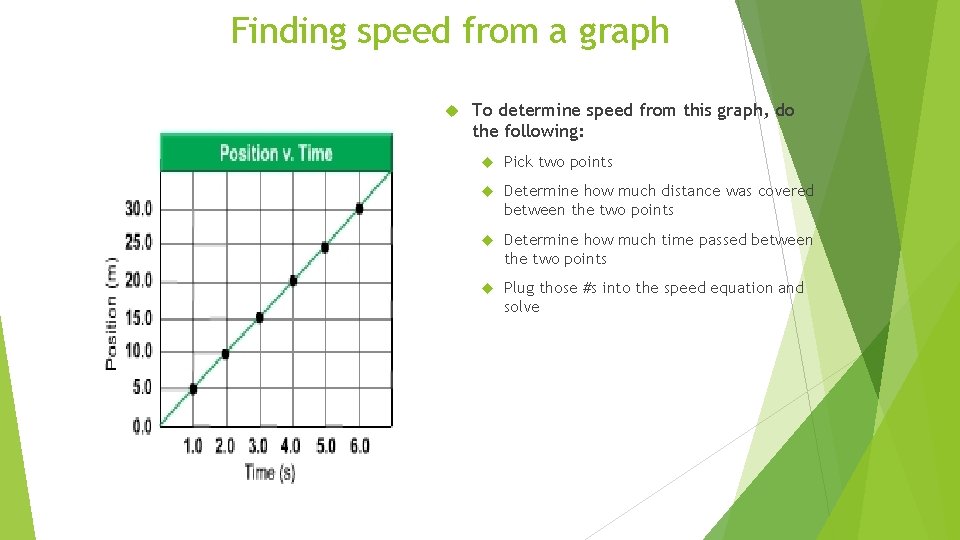
Finding speed from a graph To determine speed from this graph, do the following: Pick two points Determine how much distance was covered between the two points Determine how much time passed between the two points Plug those #s into the speed equation and solve

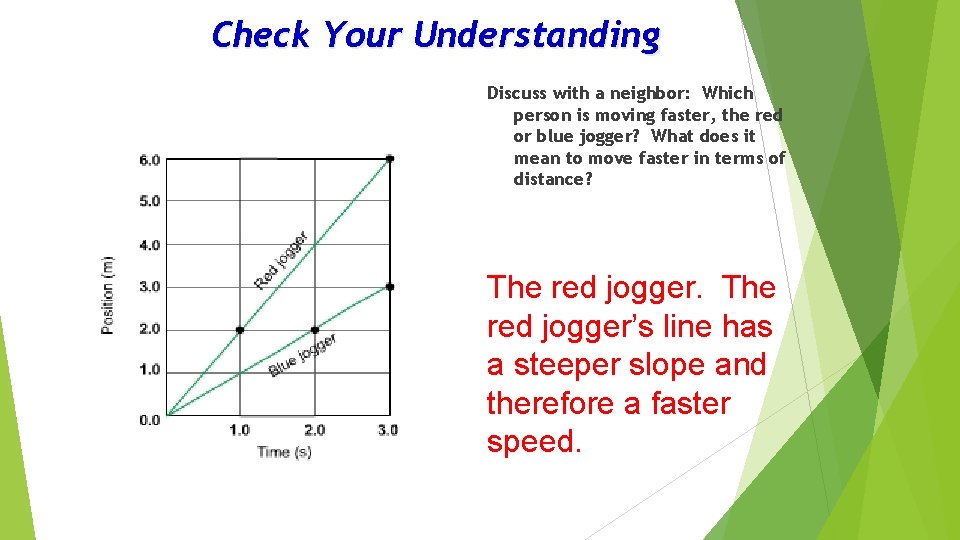
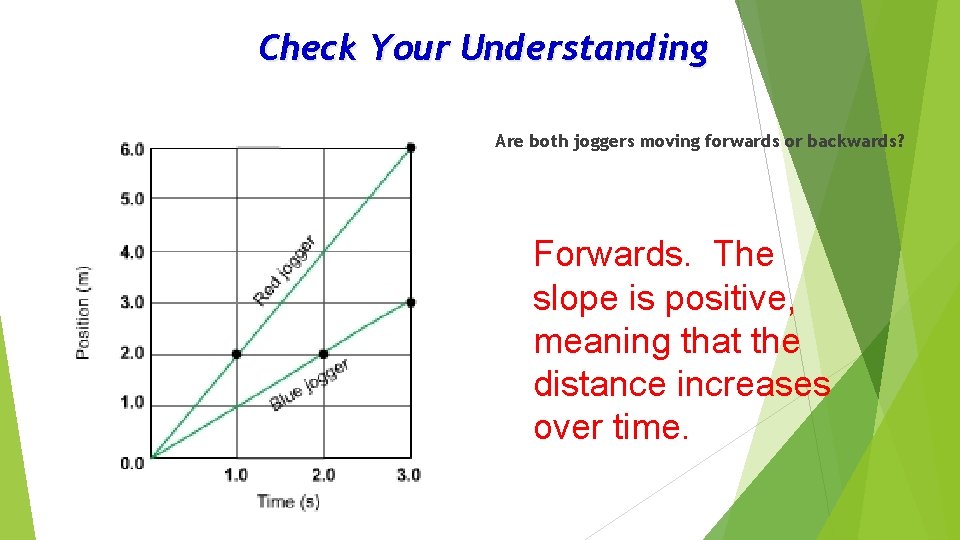
Check Your Understanding Discuss with a neighbor: Which person is moving faster, the red or blue jogger? What does it mean to move faster in terms of distance? The red jogger’s line has a steeper slope and therefore a faster speed.

Check Your Understanding Are both joggers moving forwards or backwards? Forwards. The slope is positive, meaning that the distance increases over time.

Three types of Acceleration Positive acceleration Increase in velocity Speeding Negative acceleration Decrease Slowing Change with up in velocity down in direction or without velocity change

Doing the math To find acceleration: A = ∆V (also written as (Vf – Vi) ∆t ∆ is the greek letter delta and means “the change in” To find the change in velocity: final velocity of the object (Vf) minus initial velocity of the object (Vi) To find the change in time: final time of the object’s motion (tf) minus initial time of the object (ti)

Some words to look out for Zero words Words that either mean the objects starts at rest (not in motion) or stops its motion Stop At rest At a standstill

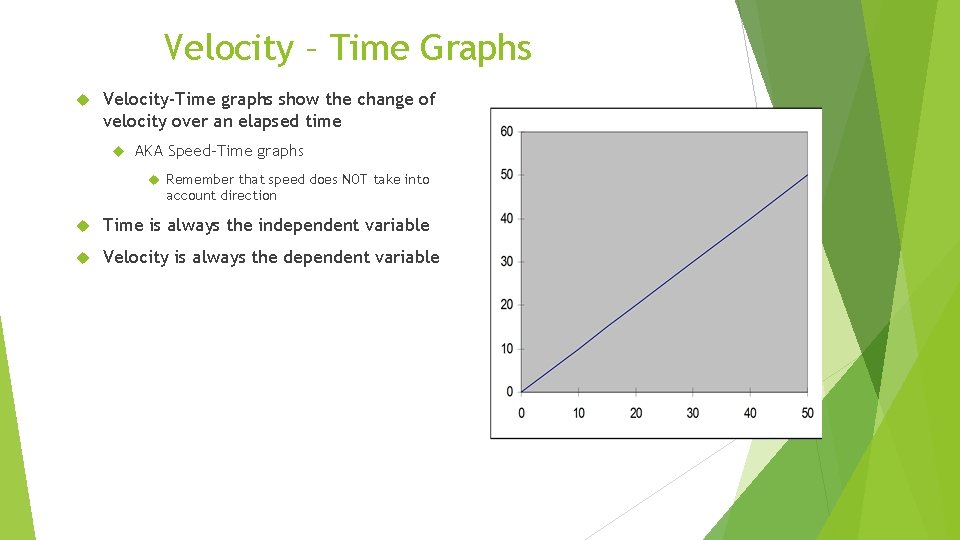
Velocity – Time Graphs Velocity-Time graphs show the change of velocity over an elapsed time AKA Speed-Time graphs Remember that speed does NOT take into account direction Time is always the independent variable Velocity is always the dependent variable

The slope of a Velocity-Time graph is equal to acceleration Slope = rise/run Slope = change in velocity / time a = Δv / t The steeper the slope, the faster the acceleration Remember acceleration can be speeding up, slowing down, or sharp turns A positive slope is speeding up and moving forward A negative slope is EITHER slowing down OR moving backwards A zero slope means that the velocity is NOT changing, meaning that the object is moving at the same speed in the same direction

Free Fall Consider an apple falling from a tree. We know that it starts at rest and gains speed as it falls, or accelerates. Gravity causes the apple to accelerate downward and is said to be in free fall. Free fall: gravity when an object is only affected by SI unit: m/s 2 ( for acceleration due to gravity) Ex: g = 10 m/s 2 on Earth. The letter g represents the acceleration due to gravity.

Equation: v = gt v = velocity or speed (m/s) g = acceleration due to gravity (10 m/s 2 on Earth) t = elapsed time (s) **Hint - as soon as you see any of the following phrases in a word problem, write g = 10 m/s 2 for a given: free fall, falling, dropped, thrown** thrown

Because an object in free fall increases the rate of distance covered every second, we cannot use v =d/t. Equation: d d=½ 2 gt = distance (m) g = acceleration due to gravity (10 m/s 2 on Earth) t = elapsed time (s)

Now consider an object thrown straight up. It will continue to move straight up, then it comes back down. At the highest point, the object changes its direction and the objects instantaneous speed is 0 m/s. Whether the object is moving up or down, the acceleration of the object is always 10 m/s 2.

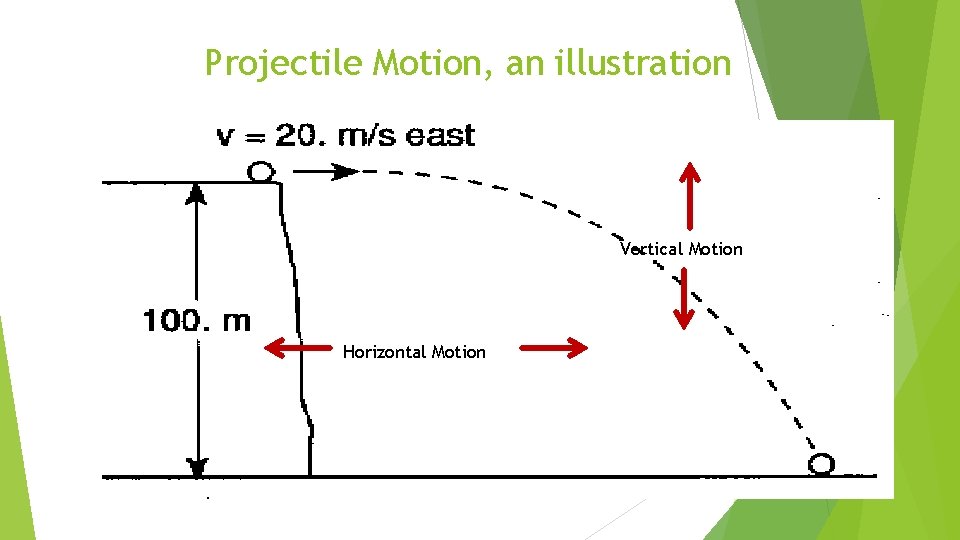
Projectile Motion, an illustration Vertical Motion Horizontal Motion

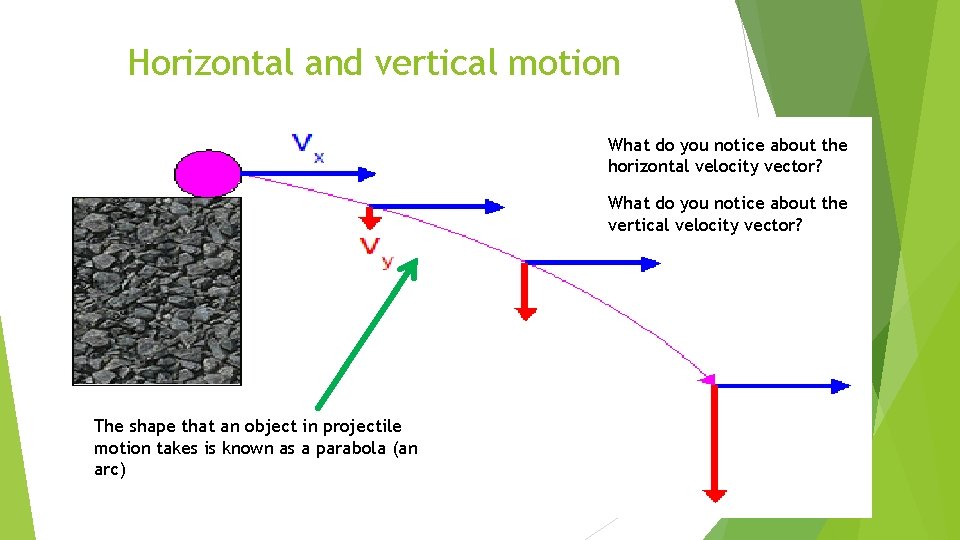
Horizontal motion (X) As the object leaves the cliff, it does so with an initial horizontal velocity The only way to change this velocity is to put some sort of new force (push or pull) on the object Ignoring air resistance, there is no other force affecting the object so it’s horizontal velocity does not change So the object continues to move forward at the same speed the entire time it falls

Vertical motion (Y) Remember that in projectile motion, the object is in free fall So as soon as it leaves the cliff, gravity is pulling the object down Acceleration due to gravity affects vertical speed causing it to increase by 10 m/s/s

Horizontal and vertical motion What do you notice about the horizontal velocity vector? What do you notice about the vertical velocity vector? The shape that an object in projectile motion takes is known as a parabola (an arc)

When you are solving projectile motion problems… If you are solving for horizontal motion (x direction), only use: V=d t If you are solving for vertical motion (y direction), only use: V = gt or d = 1/2 gt 2 This is because gravity does not effect horizontal motion This is because gravity is the only thing that affects vertical motion The amount of time that an object falls will be the same for both horizontal and vertical motion - This is because no matter if an object is falling or if it has been thrown, it will fall towards the earth with the same acceleration (10 m/s/s) due to gravity

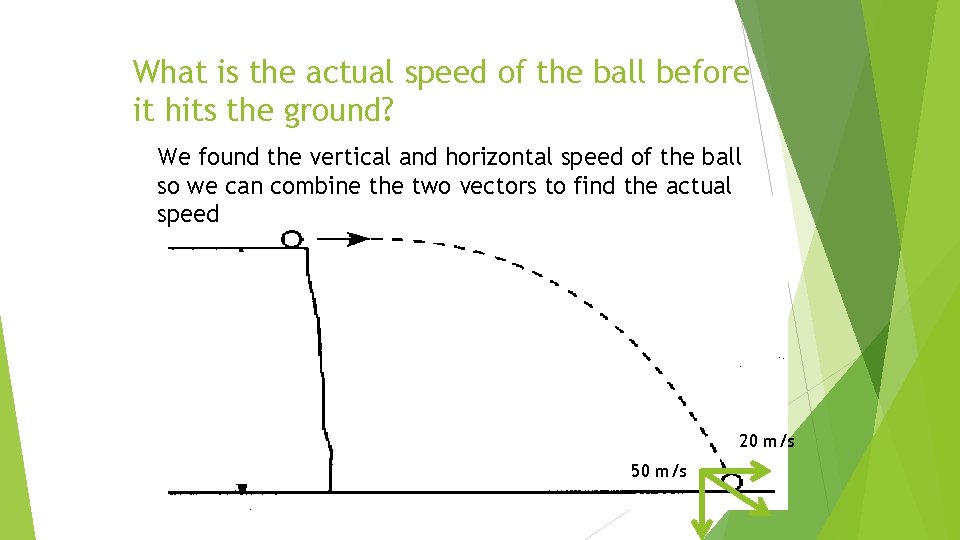
What is the actual speed of the ball before it hits the ground? We found the vertical and horizontal speed of the ball so we can combine the two vectors to find the actual speed 20 m/s 50 m/s

Vectors A vector quantity is a quantity that has both magnitude and a direction in space Examples of Vector Quantities: Displacement Velocity Acceleration Force

Resultant of Two Vectors The resultant is the sum or the combined effect of two vector quantities Vectors in the same direction: 6 N 4 N = 10 m If two vectors are in the same direction, add them together and keep that direction 6 m 4 m Vectors in opposite directions: 6 m s-1 10 m s-1 = 4 m s-1 6 N 10 N 4 N = If two vectors are in the opposite direction, subtract them and keep the direction of the larger vector

Newton’s First Law Newton’s st 1 Law of Motion: An object in motion will continue in motion at the same speed and in the same direction or an object at rest will remain at rest until another force changes its motion aka the Law of Inertia An object at rest stays at rest; an object in motion stays in motion Ex: An object moving in space will keep moving at a constant speed

Inertia: the property of a body to resist change in motion. § Things tend to keep doing what they’re already doing. § Unit: kilograms (kg) § Ex: you keep moving when a car stops b/c you have inertia (you were moving with the car, but the brakes didn’t affect you)

Mass and Inertia Mass: the amount of matter present in an object § The more mass, the greater the inertia…and the greater the force it takes to change the state of motion. § Mass remains the same wherever you are § Units: kilograms (kg) § Ex: your mass is 10 kg on Earth and on the moon

Newton’s Second Law of Motion Newton’s nd 2 Law: The acceleration on an object is directly proportional to the magnitude of the net force, and is inversely proportional to the mass of the object.

Weight: Weight the force of gravity on an object’s mass § Ex: your weight on Earth is 100 N, but on the moon it is 16 N § Unit: Newtons (N) § Equation: W = mg W = weight (N) m = mass (kg) g = acceleration due to gravity (10 m/s 2)

§ Forces produce accelerations § Ex: The harder you push something, the faster it goes § Equation: a = F/M F = force (N) m = mass (kg) a = acceleration (m/s 2)

Net force is directly proportional to acceleration This means that as one increases, the other increases by the same amount § 2 F = 2 a § 3 F = 3 a

Mass and Acceleration Mass and acceleration are inversely proportional As one increases, the other decreases by the same amount § 2 m, ½a § ½m, 2 a § 10 m, 1/10 a § 1/10 m, 10 a

Friction �Two or more objects in contact moving past each other will slow each other down. The force which causes them to slow down is friction. Friction: the force that acts to resist the relative motion of objects in contact. § Friction is a force between surfaces that depends on the materials in contact with each other and how much force is pushing the objects together § Unit: Newtons (N) § Ex: Tires on the road, rubbing your hands together, air resistance

Newton’s Third Law Newton’s rd 3 Law of Motion: Whenever one object exerts a force on a second object, the second object exerts an equal and opposite force on the first object. aka The Law of Action and Reaction § Ex: You hit the wall, but the wall is hitting you back (hence why it hurts) §

One force is the action force and the other force is the reaction force. Neither coexists without the other. You can’t touch something without being touched.

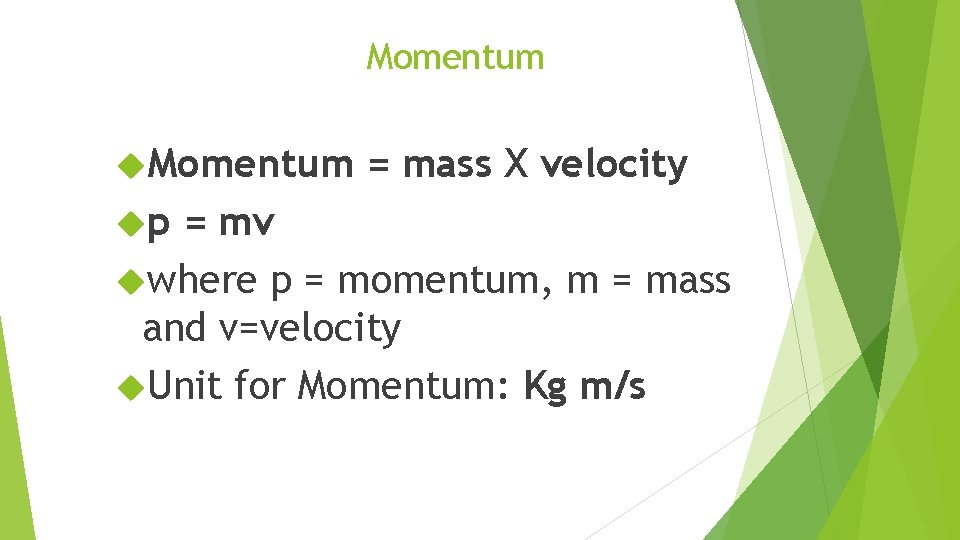
Momentum p = mass X velocity = mv where p = momentum, m = mass and v=velocity Unit for Momentum: Kg m/s

Impulse Equation Impulse is found by multiplying the force applied to an object by the amount of time the force was applied Impulse = force x time Impulse = Ft Unit for impulse is N∙s Remember that impulse = change in momentum (∆mv) So… Ft = ∆mv

How can Impulse increase momentum? To increase momentum you want to apply the greatest force over the longest possible time Ex: hitting a golf ball or a baseball Swing with as much power as possible (greatest force) Follow through once you’ve made contact (longest time)

How can impulse decrease momentum? By extending the time of impact Impact is the actual force being applied You are increasing the time it takes for momentum to be brought down to zero Ex: air bags When air bags deploy, it takes you longer to hit the dashboard creating less of a force when do you hit it Ex: Running into a haystack instead of a brick wall You will create the same amount of impulse hitting them, but… For the haystack: F t For the brick wall: F t

What is conservation of momentum? The momentum of a system remains the same if there are no external forces We can illustrate this concept using collisions between objects The momentum of the objects before the collision is equal to the momentum of the objects after the collision MVtotal = Mvtotal MV + MV = MV + MV

Elastic collisions occur when two or more objects collide without any being deformed or creating heat The objects bounce off of each other and transfer their momentum Before 2 m/s Collision 0 m/s 2 m/s 1 m/s after 0 m/s 2 m/s 1 m/s Elastic Collisions 2 m/s

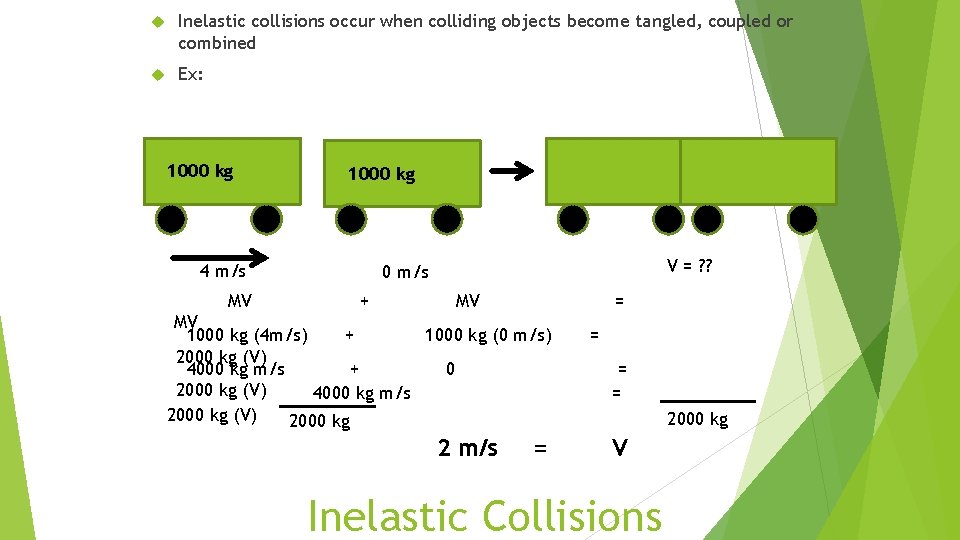
Inelastic collisions occur when colliding objects become tangled, coupled or combined Ex: 1000 kg 4 m/s MV V = ? ? 0 m/s + MV = MV 1000 kg (4 m/s) + 1000 kg (0 m/s) 2000 kg (V) 4000 kg m/s + 0 2000 kg (V) 4000 kg m/s 2000 kg (V) 2000 kg 2 m/s = = 2000 kg V Inelastic Collisions

A 2 kg goldfish is swimming towards the right at 5 m/s when a 15 kg puffer fish swims up and eats it. The pufferfish was swimming towards the left at 7 m/s. What is the final velocity of the two fish after the puffer fish eats the goldfish? MV + 2 kg (5 m/s) 10 kg m/s + + 115 kg m/s MV = 15 kg (7 m/s) = 105 kg m/s = = 17 kg 6. 76 m/s = V MV 17 kg (V) 17 kg