Calculating Speed from a DistanceTime Graph Average Speed

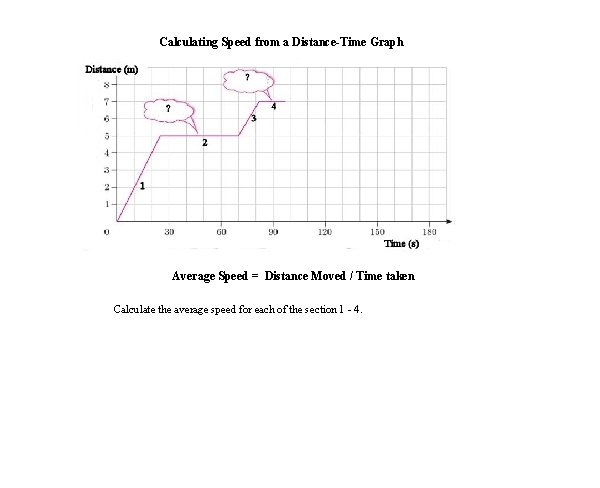
Calculating Speed from a Distance-Time Graph Average Speed = Distance Moved / Time taken Calculate the average speed for each of the section 1 - 4.

Difference between Speed and Velocity Speed is a vector quantity. It only has a size. It has no direction For example 5 m/s or 100 m/s Velocity has direction and magnitude. For example a velocity of 5 m/s due North or 30 m/s due East Velocity can be negative or positive. The sign of the velocity will indicate the direction of the velocity

Representing Velocity Positive direction 5 m/s This car is travelling at a velocity of 5 m/s due West This car is travelling at 2 m/s due South OK. . they have no drivers. . .

Representing Velocity is represented by a VECTOR ARROW The direction of the arrow shows the direction of the velocity The length of the arrow represents the size of the velocity Now try this: Draw the velocity vectors for the following: (a) A train travelling at 50 m/s due East (b) A car travelling at 10 m/s due South (c) A marathon runner at 2 m/s due West.

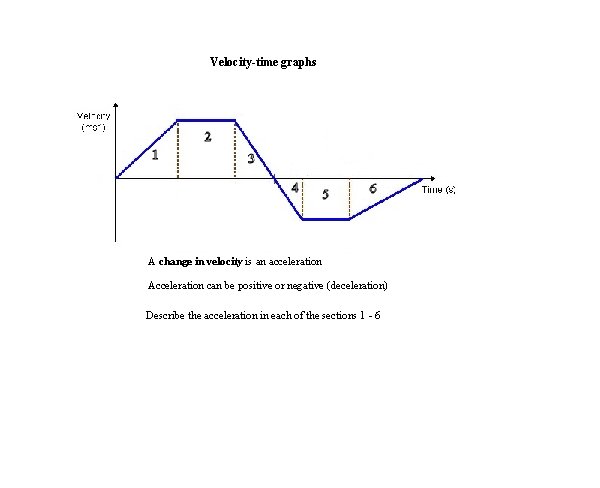
Velocity-time graphs A change in velocity is an acceleration Acceleration can be positive or negative (deceleration) Describe the acceleration in each of the sections 1 - 6

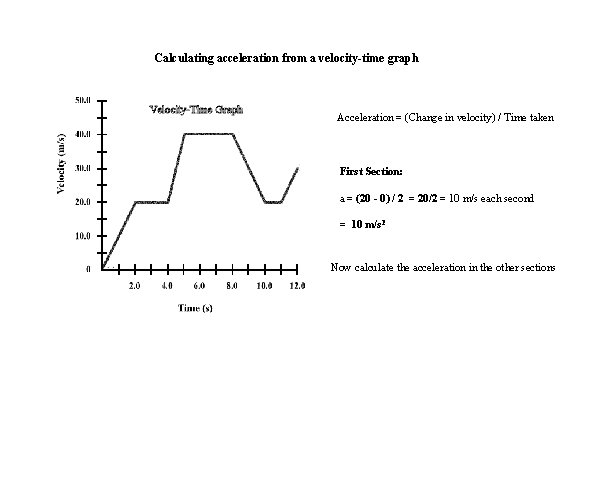
Calculating acceleration from a velocity-time graph Acceleration = (Change in velocity) / Time taken First Section: a = (20 - 0) / 2 = 20/2 = 10 m/s each second = 10 m/s 2 Now calculate the acceleration in the other sections

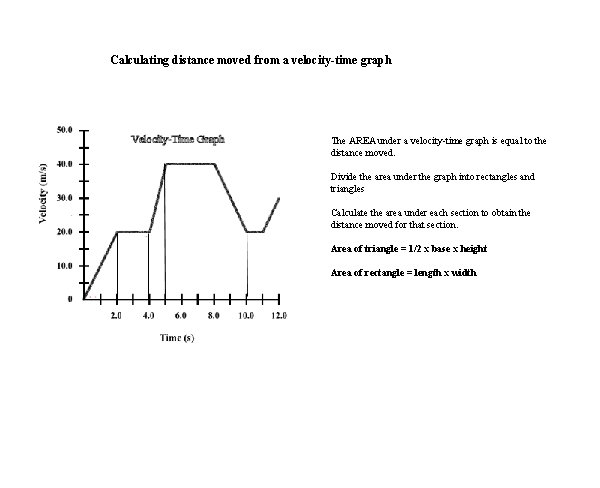
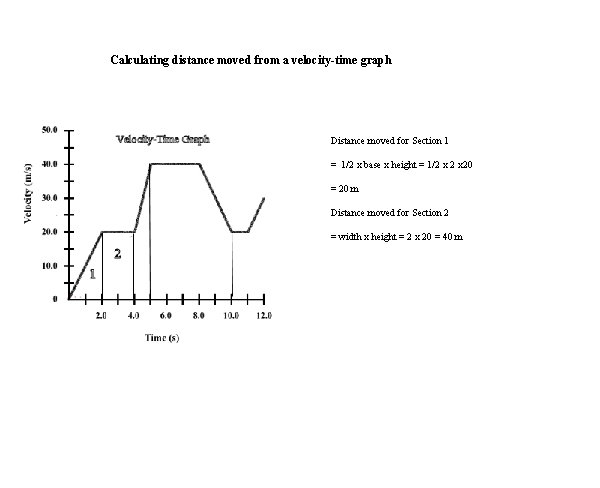
Calculating distance moved from a velocity-time graph The AREA under a velocity-time graph is equal to the distance moved. Divide the area under the graph into rectangles and triangles Calculate the area under each section to obtain the distance moved for that section. Area of triangle = 1/2 x base x height Area of rectangle = length x width

Calculating distance moved from a velocity-time graph Distance moved for Section 1 = 1/2 x base x height = 1/2 x 20 = 20 m Distance moved for Section 2 = width x height = 2 x 20 = 40 m