Sistemas Ecuaciones Lineales Teora Definicin Un sistema de

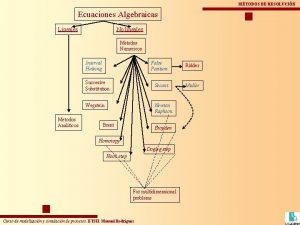
Sistemas Ecuaciones Lineales Teoría

Definición: Un sistema de m ecuaciones lineales con n incógnitas (en R): Como paso previo a resolverlo necesitamos saber: - si hay solución única. - si no hay solución. - si hay infinitas soluciones.

Matrices del sistema: Matriz de coeficientes Matriz de términos independientes Matricialmente el sistema se expresa: M. X = B

Sistema de Cramer: Un sistema del tipo M. X = B se llama Sistema de Cramer si cumple las dos condiciones: 1) n = m (la matriz M es cuadrada). 2) La matriz M es inversible. En este caso siempre existe solución única: X = M-1. B Pero suele darse una expresión más sencilla (computacionalmente)

Siendo los Mii los adjuntos de los elementos de M, entonces: Teniendo en cuenta:

Por lo tanto: los valores de la solución pueden computarse así:

Un ejemplo: Sea el sistema lineal 2 x + y – 3 z = 5 3 x – 2 y +2 z = 5 5 x – 3 y – z = 16 Resolución: Es sistema de Cramer: M es cuadrada y |M| = 26.

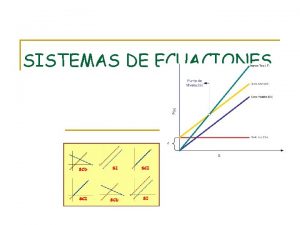
Clasificación de sistemas lineales: Sea un sistema lineal de ecuaciones: Consideramos las dos matrices:

* Teorema de Rouche-Frobenius. Sea un sistema lineal (de m ecuaciones con n incógnitas): I) Sistema compatible (hay soluciones) r(M) = r(M’) II) Sistema incompatible (no hay soluciones) r(M) r(M’). ____________________ → I) Para el caso de sistema compatible tenemos: a) Sistema compatible determinado: r(M) = r(M*) = n --- entonces la solución del sistema es única -- --- se trata de un sistema de Cramer ------- b) Sistema compatible indeterminado: r(M) = r(M*) = h < n --- solución dependiente de n-h parámetros -- En este último caso, supongamos la existencia de un menor de orden h, tal que

Eliminamos las ecuaciones innecesarias, nos queda: Es decir: Que se resuelve como sistema de Cramer.

Sistemas lineales homogéneos. Cuando los términos independientes son nulos. -Admiten siempre la solución trivial: x 1=0, x 2=0, ………, xn=0 -Si r(M)<n el sistematiene infinitas soluciones: r(M) = r(M’) → Sistema compatible indeterminado

Ejemplo 1: Clasificar el siguiente sistema lineal y, si fuera posible, resolverlo: x – y + 3 z = 3 x + 2 y – z = 2 2 x + y + 2 z = 5 Solución: Utilizamos el método de Gauss: F 2←F 2 -F 1 F 3←F 3 -F 1 F 3←F 3 -2 F 1 r(A) = r(A’)= 2 → Sistema compatible indeterminado

Para resolverla podemos partir de: Finalmente, podríamos hacer: z = 3λ x = 8/3 - 5 λ y = -1/3 + 4 λ z = 3 λ

Ejemplo 2: Hallar la relación que deben cumplir a, b, c , para que el sistema: 3 x + 2 y = a -2 x + 5 y = b 4 x + 9 y = c tenga una solución única: Solución: Utilizando el método de Gauss: 1. (1) F 2 ← 3 F 2 + 2 F 1 (2) F 3 ← F 3 – F 2 2. F 3 ← 3 F 3 - 4 F 1 Por tanto, el sistema tiene solución única si: -6 a - 3 b + 3 c = 0 3.

Ejemplo 1: Determinar el valor de “a” para que el sistema homogéneo: a x + y - z = 0 x + 3 y + z = 0 3 x +10 y + 4 z = 0 admita soluciones distintas de la (0, 0, 0), y resolverlo para ese valor de a.

Solución: Por tanto, |A|=0 → a =1. Para A = 1, Para resolverlo eliminamos la última ecuación: a x + y = z x + 3 y = - z x = 2λ , y = -λ , z = λ