Simplification OutofCore des modles polygonales complexes KRAEMER Petra

Simplification Out-of-Core des modèles polygonales complexes KRAEMER Petra SERROUKH Youssef TATUT Georgiana-Alina Encadré par : REUTER Patrick

Maillage n n n Approximation par morceaux par l’assemblage de facettes Modèle polygonal décrit par les coordonnées 3 D Stockage du maillage ¨ Soupe de polygones ¨ Polygones indexés

Motivation n n Informations à différentes résolutions Oversampling Traitement plus rapide du maillage (rendu, compression, analyse de la surface) Modèle trop grand pour l’affichage, traitement, transmission et stockage en mémoire central Solution : Out-of-Core Simplification

Caractéristiques d’un algorithme de simplification n n n n Préservation de la topologie Gestion d’une soupe de polygones Coût de mémoire Facilité d’implémentation et d’utilisation Encodage Transition continue Utilisation dépendante du point de vue Prise en compte des attributs Orienté erreur ou budget

Algorithme de Lindstrom n Hybride : clustering de sommets avec erreur quadratique clustering de sommets (Rossignac et Borrel ’ 93) ¨ erreur quadrique (Garland et Heckbert ’ 97) ¨

Algorithme Oo. CS 1. 2. 3. 4. 5. 6. 7. 8. pour chaque triangle t Є Tin { on calcule les coordonnées de chaque sommet définir une table de hachage dynamique de clusters pour chaque sommet vin de t définir une clé de hachage si pour un cluster donné on a pas de représentant créer un nouveau sommet vout sa matrice quadrique est initialisée à zero

Suite Algorithme Oo. CS 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. si aux moins 2 sommets de t Є un même cluster t est réduit à une arête ou à un point et mit à l’écart sinon Vout += vt Tout += t calculer la matrice quadrique Qt de t pour chaque sommet de t Qv += Qt } pour chaque cluster V calculer les coordonnées du sommet représentatif retourner (Vout , Tout ) dans un format approprié

Clustering des sommets n • Rossignac et Borrel : 1993 introduction de l’idée de simplification par Clustering. Le modèle est au préalable triangulé. L’utilisation d’une grille régulière. • Pour chaque sommet un poids est attribué. • Le sommet de représentation: • • • La somme pondérée des sommets (lisse la surface) Le sommet de poids maximal (élimine les détails)

Exemple de clustering de sommets

Quadrique (1) n Chaque cluster associé un seul sommet dit « représentatif » qui appartiendra au maillage simplifié n Problématique comment déterminer la position du sommet « représentatif » afin de minimiser l’erreur introduite par le processus de simplification n Solution utiliser une quadrique (Garland et Heckbert)

Quadrique (2) n n Chaque cluster matrice quadrique associée Qc Triangle en train d’être traité quadrique Q associée: n - vecteur de dimension 4 compose de la normale au plan défini par le triangle et le produit scalaire de ses trois sommets n Cluster de chaque sommet repartition de Q : Qc = Qc + Q n Remarque: la matrice Q décomposée:

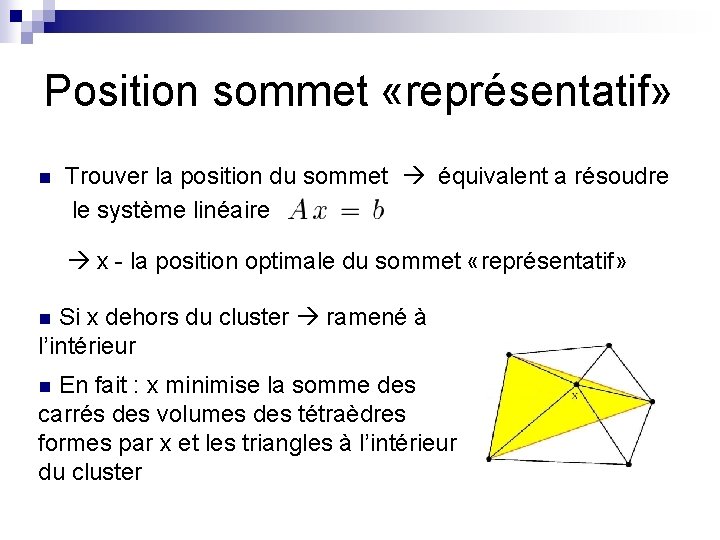
Position sommet «représentatif» n Trouver la position du sommet équivalent a résoudre le système linéaire x - la position optimale du sommet «représentatif» Si x dehors du cluster ramené à l’intérieur n En fait : x minimise la somme des carrés des volumes des tétraèdres formes par x et les triangles à l’intérieur du cluster n

Tests et résultats (1) Original Buddha 1, 087, 716 triangles Oo. CS 204, 750 triangles Oo. CS 62, 354 triangles

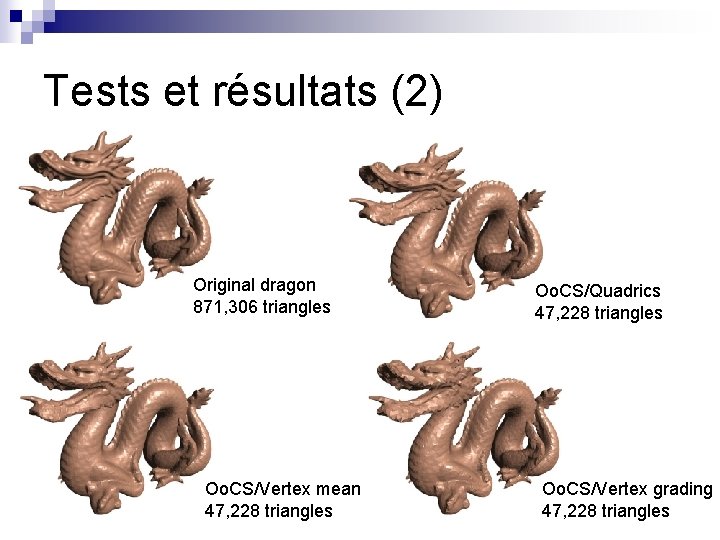
Tests et résultats (2) Original dragon 871, 306 triangles Oo. CS/Vertex mean 47, 228 triangles Oo. CS/Quadrics 47, 228 triangles Oo. CS/Vertex grading 47, 228 triangles

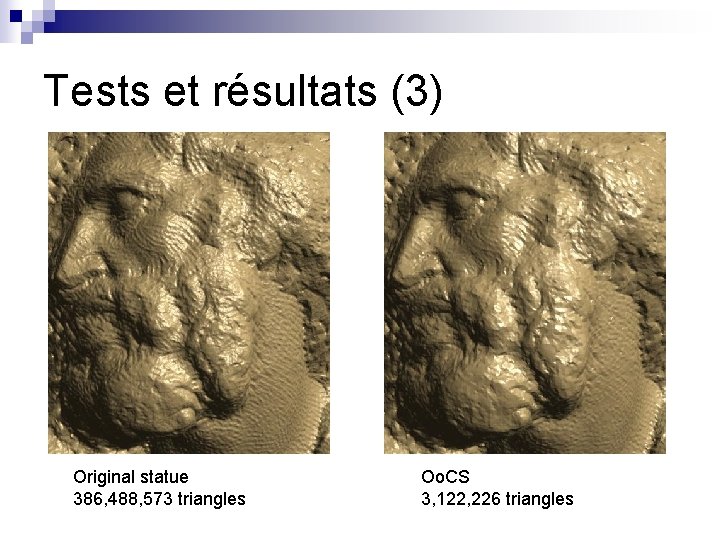
Tests et résultats (3) Original statue 386, 488, 573 triangles Oo. CS 3, 122, 226 triangles

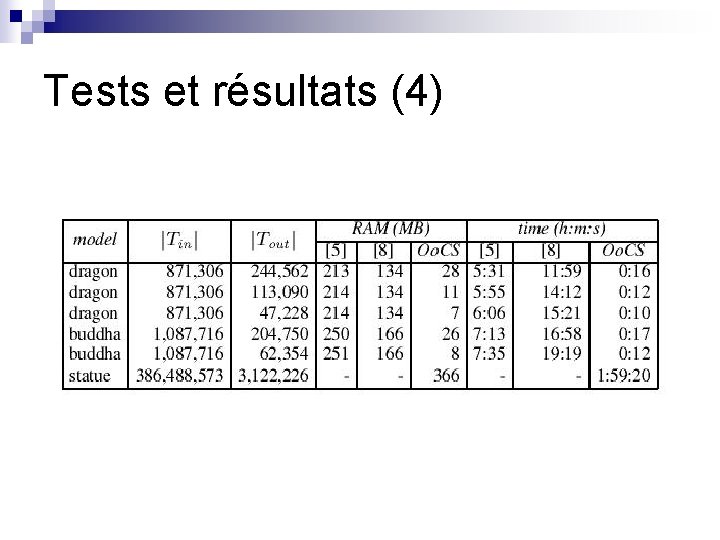
Tests et résultats (4)

Conclusion Algorithme rapide : O(n) n On a pas besoin d’espace mémoire important n Représentation du modèle d’entrée comme soupe de polygones n Facile à implémenter n

Références n n n Out-of-Core Simplification of Large Polygonal Models. Lindstrom, SIGGRAPH 2000. Surface Simplification using Quadric Error Metrics. Garland Heckbert, SIGGRAPH 1997. Fast and Memory Efficient Polygonal Simplification. Lindstrom and Turk, IEEE 1998. Geometric Simplification and compression. Rossignac, SIGGRAPH 1997. Pré-traitement de grosses données pour la visualisation interactive. Décoret, Thèse 1992.