Sharif University of Technology Department of Computer Engineering

Sharif University of Technology Department of Computer Engineering Data and Network Security Lab Elliptic Curve Cryptography Author & Instructor: Hamed Dashti Sharif University Introduction to Modern Cryptography Spring 2015 1 / 50

Outline q q What Is An Elliptic Curve? Elliptic Curve Structures o q ECDLP Elliptic Curve Cryptography ECC Diffie-Hellman Key Exchange o ECC El. Gamal Public key Cryptosystem o ECC Signature o q q Lenstra’s Elliptic Curve Factorization Algorithm Bilinear Pairing o Weil Pairing Sharif University Introduction to Modern Cryptography Spring 2015 2 / 50

What Is An Elliptic Curve? Sharif University Introduction to Modern Cryptography Spring 2015 3 / 50

What is an Elliptic Curve? q Sharif University Introduction to Modern Cryptography Spring 2015 4 / 50

Defining a group over EC q Sharif University Introduction to Modern Cryptography Spring 2015 5 / 50

Addition over EC: A visual example Sharif University Introduction to Modern Cryptography Spring 2015 6 / 50

Addition over EC: An algebraic example q Sharif University Introduction to Modern Cryptography Spring 2015 7 / 50

Doubling a point q What happens if we want to add a point P itself? Sharif University Introduction to Modern Cryptography Spring 2015 8 / 50

Example q Sharif University Introduction to Modern Cryptography Spring 2015 9 / 50

Defining the inverse of a point q q Define the inverse of P = (a, b) to be P = (a, b). We want to add P and P o q The line L is a vertical lines! Define an extra point �� that lives at infinity! Sharif University Introduction to Modern Cryptography Spring 2015 10 / 50

What is an elliptic curve: Recap q Sharif University Introduction to Modern Cryptography Spring 2015 11 / 50

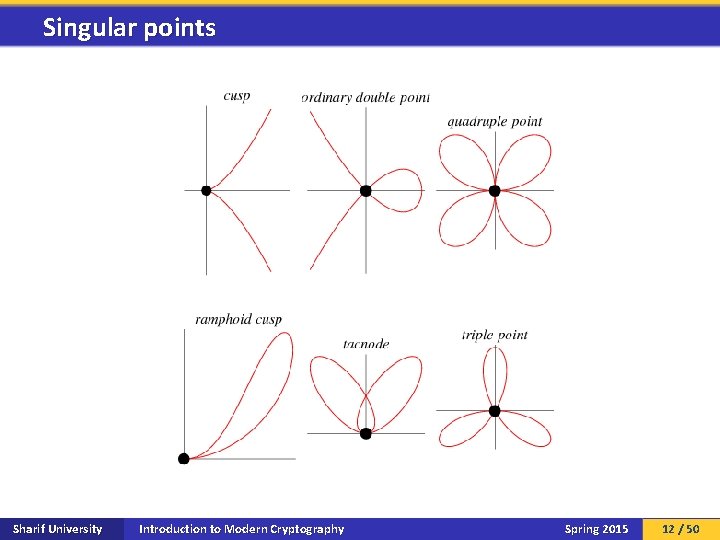
Singular points Sharif University Introduction to Modern Cryptography Spring 2015 12 / 50

Theorems about EC q Sharif University Introduction to Modern Cryptography Spring 2015 13 / 50

Theorems about EC q Sharif University Introduction to Modern Cryptography Spring 2015 14 / 50

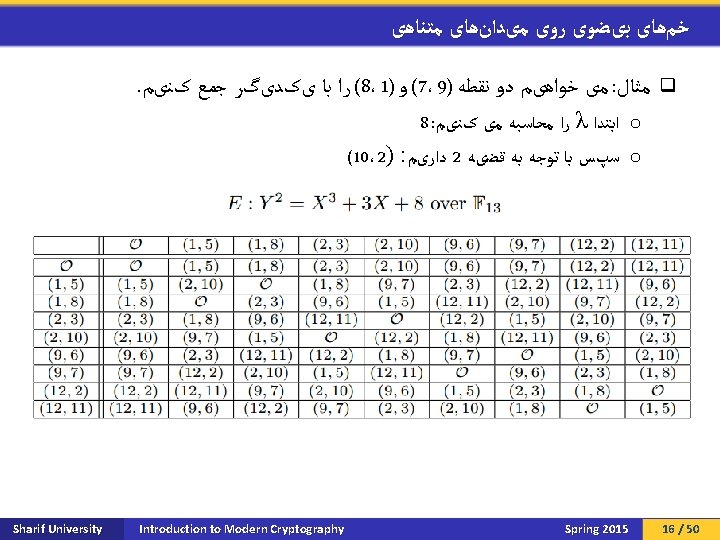
ﺧﻢﻫﺎی ﺑیﻀﻮی ﺭﻭی ﻣیﺪﺍﻥﻫﺎی ﻣﺘﻨﺎﻫی Sharif University Introduction to Modern Cryptography Spring 2015 15 / 50

ﺧﻢﻫﺎی ﺑیﻀﻮی ﺭﻭی ﻣیﺪﺍﻥﻫﺎی ﻣﺘﻨﺎﻫی q Sharif University Introduction to Modern Cryptography Spring 2015 17 / 50

Elliptic Curves over Finite Fields q Sharif University Introduction to Modern Cryptography Spring 2015 18 / 50

The Elliptic Curve Discrete Logarithm Problem (ECDLP) Sharif University Introduction to Modern Cryptography Spring 2015 19 / 50

ECDLP q Sharif University Introduction to Modern Cryptography Spring 2015 20 / 50

ECDLP q Sharif University Introduction to Modern Cryptography Spring 2015 21 / 50

ECDLP q Sharif University Introduction to Modern Cryptography Spring 2015 22 / 50

ECDLP The proof is very simple Sharif University Introduction to Modern Cryptography Spring 2015 23 / 50

Elliptic Curve Cryptography Sharif University Introduction to Modern Cryptography Spring 2015 24 / 50

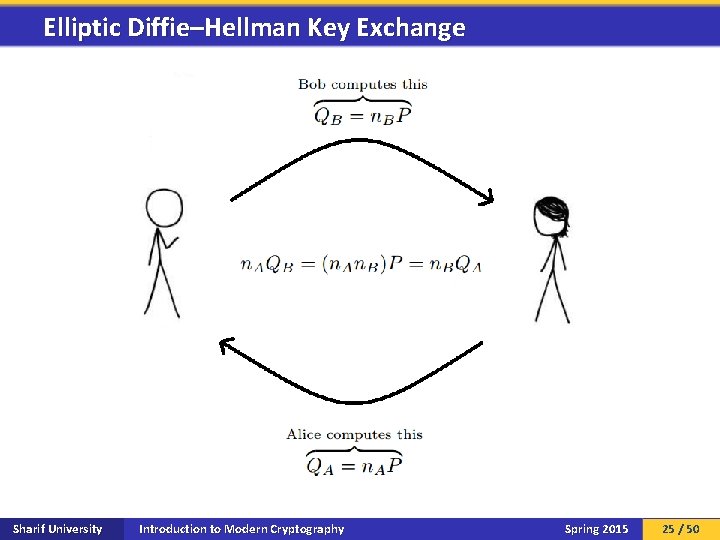
Elliptic Diffie–Hellman Key Exchange Sharif University Introduction to Modern Cryptography Spring 2015 25 / 50

Elliptic Diffie–Hellman Key Exchange Sharif University Introduction to Modern Cryptography Spring 2015 26 / 50

Elliptic Curve Diffie–Hellman Problem Sharif University Introduction to Modern Cryptography Spring 2015 27 / 50

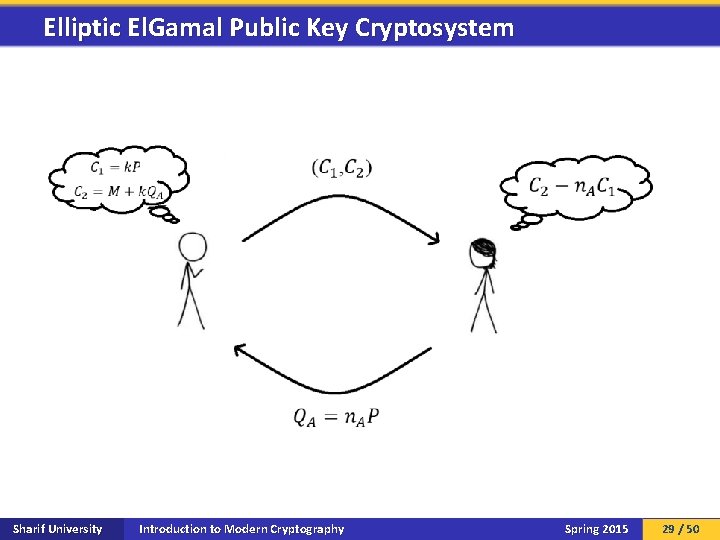
Elliptic El. Gamal Public Key Cryptosystem q Sharif University Introduction to Modern Cryptography Spring 2015 28 / 50

Elliptic El. Gamal Public Key Cryptosystem Sharif University Introduction to Modern Cryptography Spring 2015 29 / 50

Elliptic El. Gamal Public Key Cryptosystem Sharif University Introduction to Modern Cryptography Spring 2015 30 / 50

Elliptic Curve Signatures q We don’t say anything about this, now! Sharif University Introduction to Modern Cryptography Spring 2015 31 / 50

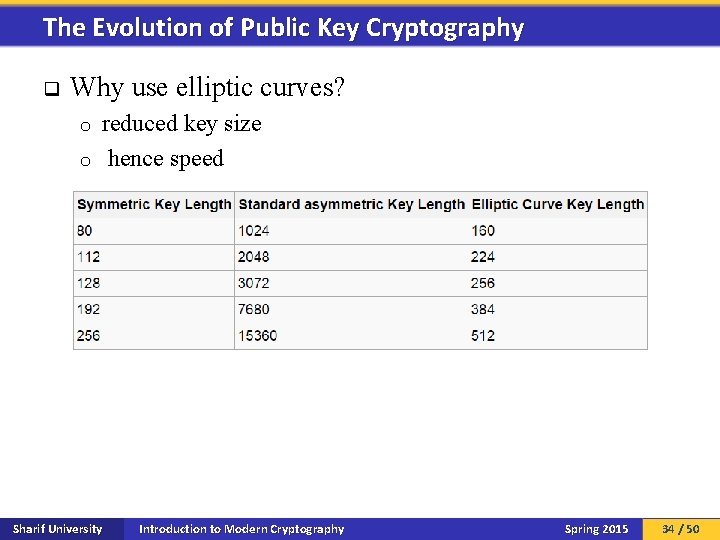
The Evolution of Public Key Cryptography Sharif University Introduction to Modern Cryptography Spring 2015 32 / 50

The Evolution of Public Key Cryptography q q What happens for RSA and El. Gamal? What about ECC? Quantum Computers will destroy everything! q Lattice-based Cryptography NTRU o GGH o Sharif University Introduction to Modern Cryptography Spring 2015 33 / 50

The Evolution of Public Key Cryptography q Why use elliptic curves? reduced key size o hence speed o Sharif University Introduction to Modern Cryptography Spring 2015 34 / 50

Lenstra’s Elliptic Curve Factorization Algorithm Sharif University Introduction to Modern Cryptography Spring 2015 35 / 50

Lenstra’s Elliptic Curve Factorization Algorithm q q q Pollard’s p 1 Algorithm It is similar to Pollard Algorithm. We’ll see an example Sharif University Introduction to Modern Cryptography Spring 2015 36 / 50

Bilinear Pairings on Elliptic Curves Sharif University Introduction to Modern Cryptography Spring 2015 37 / 50

Bilinear Pairings on Elliptic Curves q Sharif University Introduction to Modern Cryptography Spring 2015 38 / 50

Bilinear Pairings on Elliptic Curves q Sharif University Introduction to Modern Cryptography Spring 2015 39 / 50

Bilinear Pairings on Elliptic Curves q Sharif University Introduction to Modern Cryptography Spring 2015 40 / 50

ﺑﺮﺍی ﻣﻄﺎﻟﻌﻪ ﺑیﺸﺘﺮ ( )ﺧﺎﺭﺝ ﺍﺯ ﺩﺭﺱ Sharif University Introduction to Modern Cryptography Spring 2015 41 / 50

Bilinear Pairings on Elliptic Curves q The bilinear pairings that we discuss in this section are similar in that they take as input two points on an elliptic curve and give as output a number. Sharif University Introduction to Modern Cryptography Spring 2015 42 / 50

Bilinear Pairings on Elliptic Curves These fields are also sometimes called Galois fields Sharif University Introduction to Modern Cryptography Spring 2015 43 / 50

Bilinear Pairings on Elliptic Curves q Sharif University Introduction to Modern Cryptography Spring 2015 44 / 50

Rational Functions and Divisors on Elliptic Curves q In order to define the Weil and Tate pairings, we need to explain how a rational function on an elliptic curve is related to its zeros and poles. A rational function is a ratio of polynomials q Definition: Divisor of f(X) q Sharif University Introduction to Modern Cryptography Spring 2015 45 / 50

Bilinear Pairings on Elliptic Curves q Similar to one variable function, we have an associated divisor for two variable function(an elliptic curve). Sharif University Introduction to Modern Cryptography Spring 2015 46 / 50

Bilinear Pairings on Elliptic Curves Sharif University Introduction to Modern Cryptography Spring 2015 47 / 50

The Weil Pairing Definition: The Weil pairing is expressed by the equations: The Weil pairing of P and Q is the quantity Sharif University Introduction to Modern Cryptography Spring 2015 48 / 50

The Weil Pairing Sharif University Introduction to Modern Cryptography Spring 2015 49 / 50

The Tate Pairing Sharif University Introduction to Modern Cryptography Spring 2015 50 / 50