Sharif University of Technology Department of Computer Engineering

Sharif University of Technology Department of Computer Engineering Data and Network Security Lab A Primer on Computational Number Theory Author & Instructor: Mohammad Sadeq Dousti Sharif University Introduction to Modern Cryptography Spring 2015 1 / 45

Copyright Notice q q These set of slides are licensed under Creative Commons Attribution-Non. Commercial-Share. Alike (CC BY-NC-SA) 4. 0. Basically, this license allows others to use the slides verbatim, and even modify and incorporate them into their own work, as long as: 1. 2. 3. q They credit the original author(s); Their work is used non-commercially; They license their work under CC BY-NC-SA 4. 0. For further information, please consult: o o https: //creativecommons. org/licenses/by-nc-sa/4. 0 https: //creativecommons. org/licenses/by-ncsa/4. 0/legalcode Sharif University Introduction to Modern Cryptography Spring 2015 2 / 45

Outline q Basics of Number Theory Finding modular multiplicative inverse o Chinese Remainder Theorem (CRT) o ℤn* and Euler’s totient function o q q Fermat’s Little Theorem (FLi. T) Primes & Primality testing Lucas test o Miller–Rabin test o q Quadratic Residuosity Legendre Symbol o Jacobi Symbol o Solovay–Strassen primality testing o Blum integers o Sharif University Introduction to Modern Cryptography Spring 2015 3 / 45

Basics of Number Theory Sharif University Introduction to Modern Cryptography Spring 2015 4 / 45

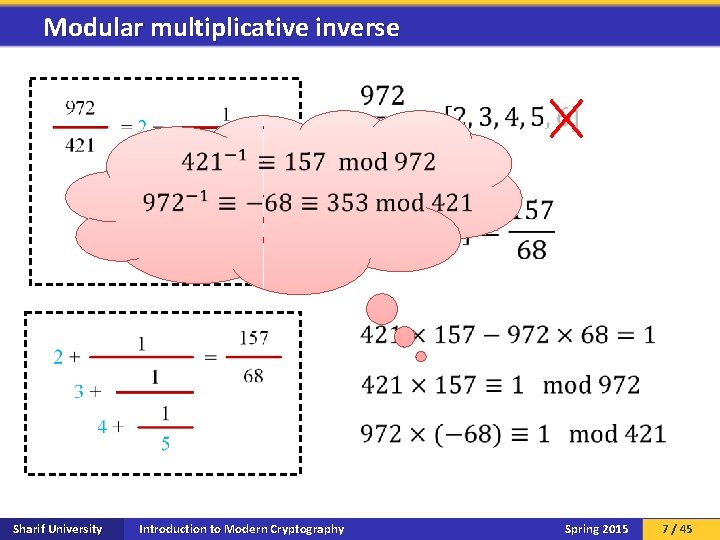
Euclidean algorithm q Find the GCD of 972 and 421. GCD Sharif University Introduction to Modern Cryptography Spring 2015 5 / 45

Continued fractions To get inverses, remove this! Sharif University Introduction to Modern Cryptography Spring 2015 6 / 45

Modular multiplicative inverse Sharif University Introduction to Modern Cryptography Spring 2015 7 / 45

Modular multiplicative inverse (Cont’d) q Sharif University Introduction to Modern Cryptography Spring 2015 8 / 45

Chinese Remainder Theorem (CRT) q The solution exists and is unique (mod M). Sharif University Introduction to Modern Cryptography Spring 2015 9 / 45

CRT: Simple Example q Sharif University Introduction to Modern Cryptography Spring 2015 10 / 45

Multiplicative group of integers modulo n q A group is an algebraic structure. o q q We’ll study groups later. A group is multiplicative if its operator is multiplication. For any n ℕ, let ℤn* denote the set: {m ℕ | 1 m n and (m, n) = 1} ℤn* is the multiplicative group of integers modulo n. The only operation of ℤn* is multiplication modulo n. Sharif University Introduction to Modern Cryptography Spring 2015 11 / 45

Examples q q q q q ℤ 2* = {1} ℤ 3* = {1, 2} ℤ 5* = {1, 2, 3, 4} ℤ 6* = {1, 5} ℤ 7* = {1, 2, 3, 4, 5, 6} ℤ 8* = {1, 3, 5, 7} ℤ 9* = {1, 2, 4, 5, 7, 8} ℤ 10* = {1, 3, 7, 9} … Sharif University Introduction to Modern Cryptography Spring 2015 12 / 45

Euler’s totient function q q The number of elements in ℤn* can be computed based on the inclusion-exclusion principle. Example: Let n = pq, where p and q are primes. There are n = pq numbers in {1, …, n} o q of which are multiples of p. o p of which are multiples of q. o 1 of which is a multiple of both p and q. In general, Euler’s totient function is computed as follows (requires o |ℤpq*| = pq p q + 1 = (p 1) prime factorization of n): o q q Euler defined a general function, φ(n), such that φ(n) = |ℤn*|. φ(n) is often called Euler’s totient function. Sharif University Introduction to Modern Cryptography Spring 2015 13 / 45

A Primer on Computational Number Theory Sharif University Introduction to Modern Cryptography Spring 2015 14 / 45

Definition q [Wikipedia]: In mathematics and computer science, computational number theory, also known as algorithmic number theory, is the study of algorithms for performing number theoretic computations. [Yan 13, p. 15] Sharif University Introduction to Modern Cryptography Spring 2015 15 / 45

Fermat’s Little Theorem (FLi. T) q [Wikipedia] Pierre de Fermat first stated theorem in a letter dated October 18, 1640, to his friend and confidant Frénicle de Bessy as the following: p divides ap − 1 whenever p is prime and a is coprime to p. Sharif University Introduction to Modern Cryptography Spring 2015 16 / 45

Example q The following can be computed extremely fast on a computer: o q Based on FLi. T, 110619 is not a prime. o q We proved this without even knowing the factorization of 110619! 414 ≡ 1 o q 2110618 ≡ 73750 (mod 110619) But 15 is not a prime. 26 ≡ 1 o (mod 15) (mod 7) And 7 is a prime. Sharif University Introduction to Modern Cryptography A primality testing algorithm with one-sided error: 1. Pick a random a ℤn* 2. compute an 1 (mod n) 3. If the result is not 1, then output COMPOSITE. 4. Output TEST FAILS. Spring 2015 17 / 45

Primality Testing Sharif University Introduction to Modern Cryptography Spring 2015 18 / 45

Lucas primality test q q q Let n > 1 be an integer. Let Q(m) denote the set of prime factors of m. n is prime if there exists 1 a n, such that: an − 1 ≡ 1 (mod n) 2. a(n − 1)/q ≢ 1 (mod n) for all q Q(n 1) 1. THEOREM 1: A prime p has at least φ(p 1) certificates in ℤp*. q Every composite integer has a short certificate for Here, φ(p 1) is the number of generators of ℤp*. compositeness (i. e. , its prime factors). q Pratt certificates: a and Q(n 1) certify the primality of n. THEOREM 2: For all n we have φ(n) = (n / log n). q Especially useful when there were no known efficient primality tests. COROLLARY: Given Q(p 1), Lucas primality test is efficient. Sharif University Introduction to Modern Cryptography Spring 2015 19 / 45

Example q 3 does not certify 11: 310 ≡ 1 (mod 11) o 32 ≡ 9 (mod 11) o 35 ≡ 1 (mod 11) o q But 2 certifies 11: 210 ≡ 1 (mod 11) o 22 ≡ 4 (mod 11) o 25 ≡ 10 (mod 11) o Sharif University Introduction to Modern Cryptography Spring 2015 20 / 45

Prime Certification q Pratt certificates established, for the first time, that PRIMES NP. q However, Pratt certificates cannot be computed efficiently, as they require the factorization of n 1. We next pertain to the problem of “Composite Certificates” without the need to factorize any number. Later, when we study Elliptic Curves, we will see an efficient algorithm to extract certificates for primes. q q o Atkin–Goldwasser–Kilian–Morain certificates. Sharif University Introduction to Modern Cryptography Spring 2015 21 / 45

Miller–Rabin primality test [HPS 14, p. 130] either this ≡ 1 Sharif University or one of these ≡ 1 Introduction to Modern Cryptography ≡ 1 due to FLi. T Spring 2015 22 / 45

Miller–Rabin primality test (Cont’d) [HPS 14, p. 131] THEOREM: Let n be an odd composite number. Then at least 3/4 of the numbers a between 1 and n − 1 are Miller–Rabin witnesses for n. Sharif University Introduction to Modern Cryptography Spring 2015 23 / 45

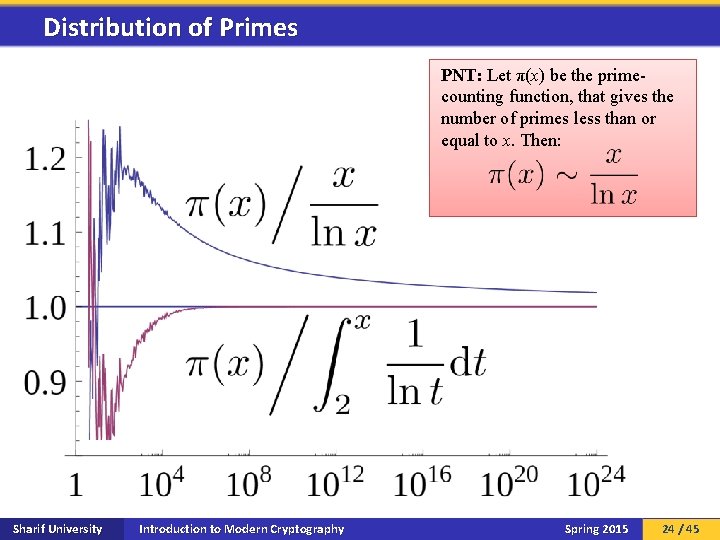
Distribution of Primes PNT: Let π(x) be the primecounting function, that gives the number of primes less than or equal to x. Then: Sharif University Introduction to Modern Cryptography Spring 2015 24 / 45

Quadratic Residuosity Sharif University Introduction to Modern Cryptography Spring 2015 25 / 45

Quadratic Residues q q is called a quadratic residue modulo n if there exists an integer x such that x 2 ≡ q (mod n). Otherwise, q is called a quadratic nonresidue modulo n. Deciding whether a given number is a quadratic residue modulo n: Easy if n is a prime; o Easy if the prime factorization of n is given; o Hard in general. o q Similarly for computing the square root. Sharif University Introduction to Modern Cryptography Spring 2015 26 / 45

Quadratic Residues (Cont’d) Let QRn and QNRn denote subsets of ℤn*, whose members are quadratic residues and nonresidues modulo n, respectively. q q Assignment: Let p be an odd prime number, and assume all computations are in ℤp*. o a QRp and b QRp a b QRp o a QRp and b QNRp a b QNRp o a QNRp and b QNRp a b QRp Proof is simple using the results of the next slide. Notice that both moduli are p. We later see that x QRpq if and only if x QRp and x QRq. Do not mix that theorem with this! Sharif University Introduction to Modern Cryptography Spring 2015 27 / 45

Odd and Even Powers of Generators q q Let p be an odd prime number , and g be any generator of ℤp*. gm QRp for even m. o q m = 2 k gm = g 2 k = (gk)2 , which is a square. gm QNRp for odd m. m = 2 k + 1 o If gm is a square, there exists x such that x 2 ≡ gm. o Using FLi. T, we have x p 1 ≡ 1, and: o o Contradicts the fact that g is a generator. Sharif University Introduction to Modern Cryptography Spring 2015 28 / 45

Square roots modulo a prime q Sharif University Introduction to Modern Cryptography Spring 2015 29 / 45

Computing square roots modulo a prime q Sharif University Introduction to Modern Cryptography Spring 2015 30 / 45

Computing square roots modulo a prime (Cont’d) q There are (at least) two efficient algorithms which can compute the square roots modulo any prime: Tonelli–Shanks algorithm o Cipolla algorithm o q The Cipolla algorithm has better asymptotic performance. The Tonelli–Shanks algorithm is better in practice. q We do not describe them here! q Sharif University Introduction to Modern Cryptography Spring 2015 31 / 45

Legendre symbol [HPS 14, p. 171] Euler’s Criterion: Multiplication Rule: Sharif University Introduction to Modern Cryptography Spring 2015 32 / 45

Quadratic Reciprocity [HPS 14, p. 172] Quadratic Reciprocity: Let p and q be odd primes. Sharif University Introduction to Modern Cryptography Spring 2015 33 / 45

Example of computing Legendre symbol Do we really need to factor? No, use Jacobi symbol. Sharif University Introduction to Modern Cryptography Because of this, powers are computed modulo 2. Spring 2015 34 / 45

Jacobi Symbol [HPS 14, p. 174] Jacobi symbol Sharif University Legendre symbols Introduction to Modern Cryptography Spring 2015 35 / 45

Laws of Jacobi Symbol [HPS 14, p. 174] q Quadratic Reciprocity holds for Jacobi Symbol as well. p and q need not be odd primes. o p and q should only be odd and positive integers. o Sharif University Introduction to Modern Cryptography Spring 2015 36 / 45

Example of computing Jacobi symbol This time, we won’t factor 15750 into 2 · 32 · 53 · 7. Sharif University Introduction to Modern Cryptography Spring 2015 37 / 45

Quadratic residuosity modulo a composite q Sharif University Introduction to Modern Cryptography Spring 2015 38 / 45

Jacobi Symbol and quadratic residuosity q Sharif University Introduction to Modern Cryptography Spring 2015 39 / 45

Solovay–Strassen primality test q Sharif University Introduction to Modern Cryptography Spring 2015 40 / 45

Useful properties q Sharif University Introduction to Modern Cryptography Spring 2015 41 / 45

Blum integers q Sharif University Introduction to Modern Cryptography Spring 2015 42 / 45

Factoring vs. extracting square roots q THEOREM: Extracting square roots modulo some Blum integer n is as hard as factoring n. q Proving one direction is easy: Given the factorization of n, extract the square root of the input a. Hint: Let x 2 ≡ a (mod p). Since p = 4 k + 3, we have x ≡ a p + 1 (mod p). o Let y 2 ≡ a (mod q). Since q = 4 j + 3, we have y ≡ a q + 1 (mod q). o Use CRT to compute the square root of a modulo n. o q Assignment: Use the hint above and present a formal reduction. Sharif University Introduction to Modern Cryptography Spring 2015 43 / 45

Factoring vs. extracting square roots (Cont’d) q Sharif University Introduction to Modern Cryptography Spring 2015 44 / 45

References [HPS 14]J. Hoffstein, J. Pipher, and J. H. Silverman. An Introduction to Mathematical Cryptography, Springer, 2014. [KL 14] J. Katz and Y. Lindell. Introduction to Modern Cryptography: Principles and Protocols, CRC Press, 2014. [Old 63] C. D. Olds. Continued Fractions, Mathematical Association of America, 1963. [Yan 13] S. Y. Yan. Computational Number Theory and Modern Cryptography. John Wiley & Sons, 2013. Sharif University Introduction to Modern Cryptography Spring 2015 45 / 45