Section 16 7 Surface Integrals Surface Integrals We









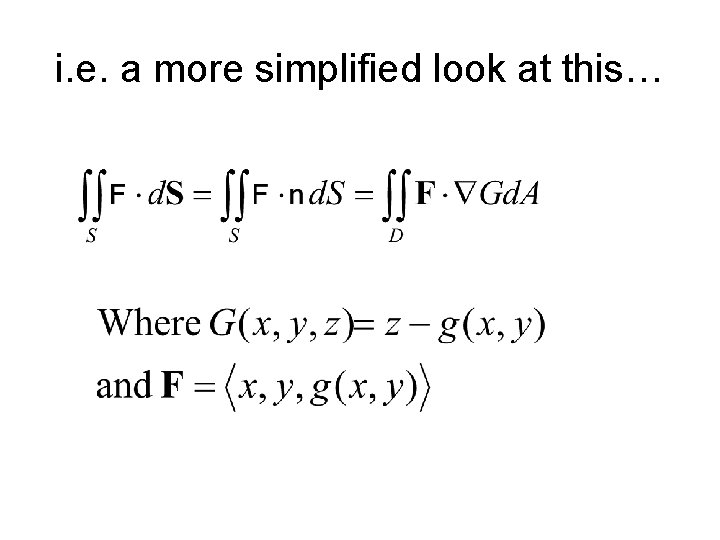


- Slides: 14

Section 16. 7 Surface Integrals

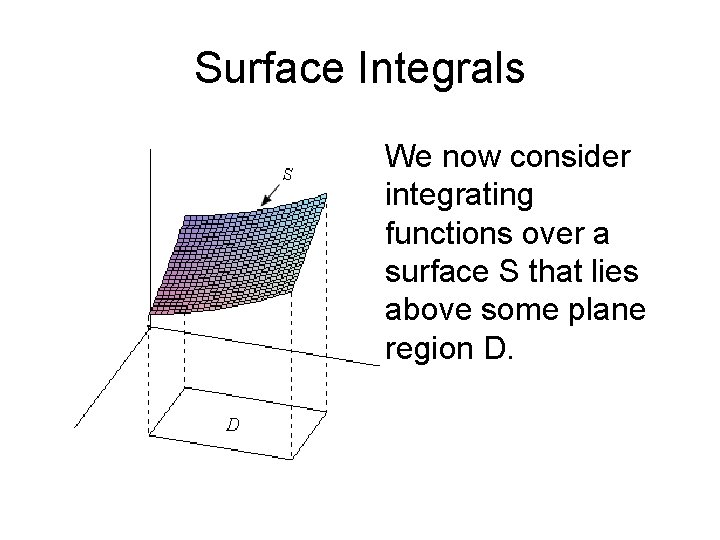
Surface Integrals We now consider integrating functions over a surface S that lies above some plane region D.

Surface Integrals Let’s suppose the surface S is described by z=g(x, y) and we are considering a function f(x, y, z) defined on S The surface integral is given by: Where d. S is the change in the surface AREA!

More useful: i. e. we convert a surface integral into a standard double integral that we can compute!

Example Evaluate Where And S is the portion of the plane 2 x+y+2 z=6 in the first octant.

Surface Integrals • We still need to discuss surface integrals of vector fields…but we need a few notions about surfaces first…. • Recall the vector form of a line integral (which used the tangent vector to the curve): For surface integrals we will make use of the normal vector to the surface!

Normal vector to a surface • If a surface S is given by z=g(x, y), what is the normal vector to the surface at a point (x, y, g(x, y)) on the surface?

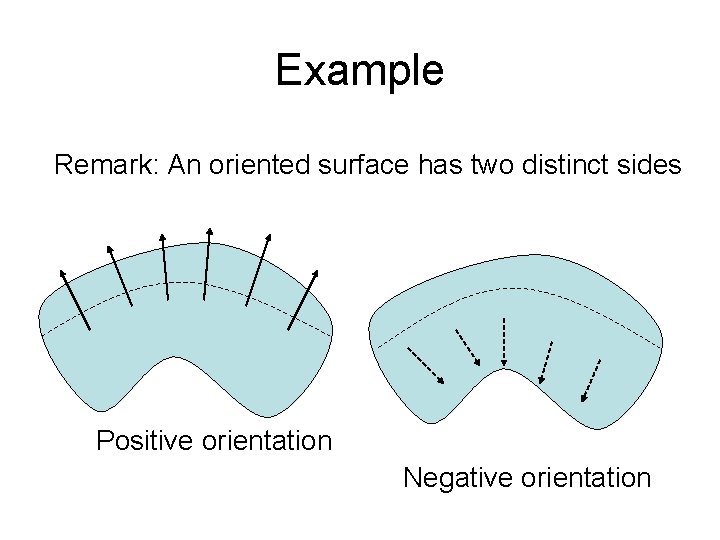
Definition: Oriented Surface • Suppose our surface has a tangent plane defined at every point (x, y, z) on the surface • Then at each tangent plane there are TWO unit normal vectors with n 1 = -n 2 • If it is possible to choose a unit normal vector n at every point (x, y, z) so that n varies continuously over S, we say S is an oriented surface

Example Remark: An oriented surface has two distinct sides Positive orientation Negative orientation

Surface Integrals of Vector Fields • If F is a continuous vector field defined on an oriented surface S with unit normal vector n, then the surface integral of F over S is This is often called the flux of F across S

Using our knowledge of the normal vector and the surface area, this can be simplified…
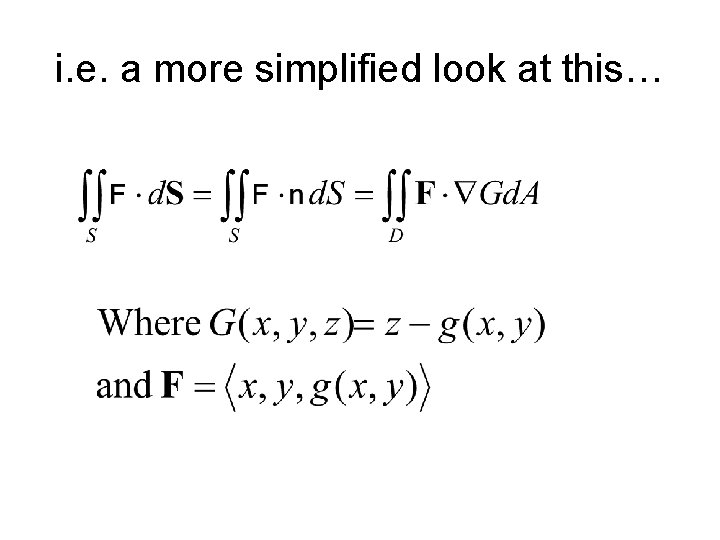
i. e. a more simplified look at this…

An application If is the density of a fluid that is moving through a surface S with velocity given by a vector field, F(x, y, z), then Represents the mass of the fluid flowing across the surface S per unit of time.

Example Let S be the portion of the paraboloid Lying above the xy-plane oriented by an upward normal vector. A fluid with a constant density is flowing through the surface S according to the velocity field F(x, y, z) = <x, y, z>. Find the rate of mass flow through S.
 S
S Surface integral
Surface integral Surface integrals
Surface integrals The substitution rule for definite integrals
The substitution rule for definite integrals Second fundamental theorem of calculus
Second fundamental theorem of calculus Sigma to integral notation
Sigma to integral notation Convolution operator symbol
Convolution operator symbol Trigonemtric integrals
Trigonemtric integrals Definite integral vs indefinite integral
Definite integral vs indefinite integral Properties of indefinite integrals
Properties of indefinite integrals Convolution sum and convolution integral
Convolution sum and convolution integral Trig integral identities
Trig integral identities Integration by substitution
Integration by substitution Slidetodoc.com
Slidetodoc.com Definition of improper integral
Definition of improper integral