SE Comp Engg Unit VI Discrete Structures Permutations








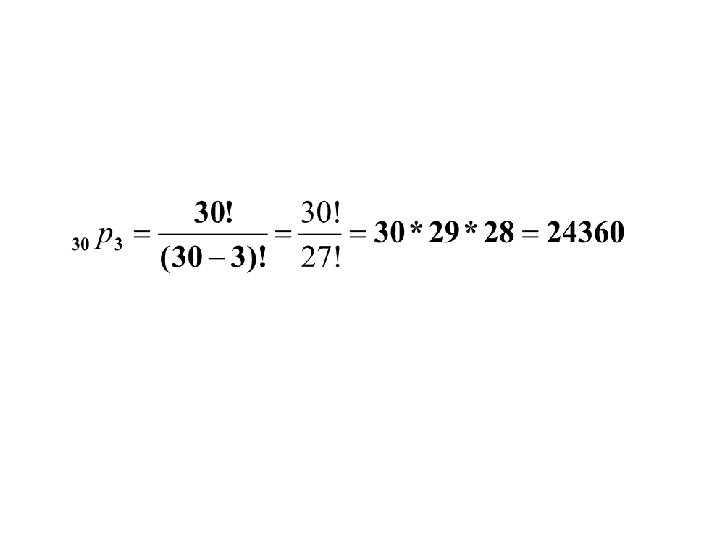







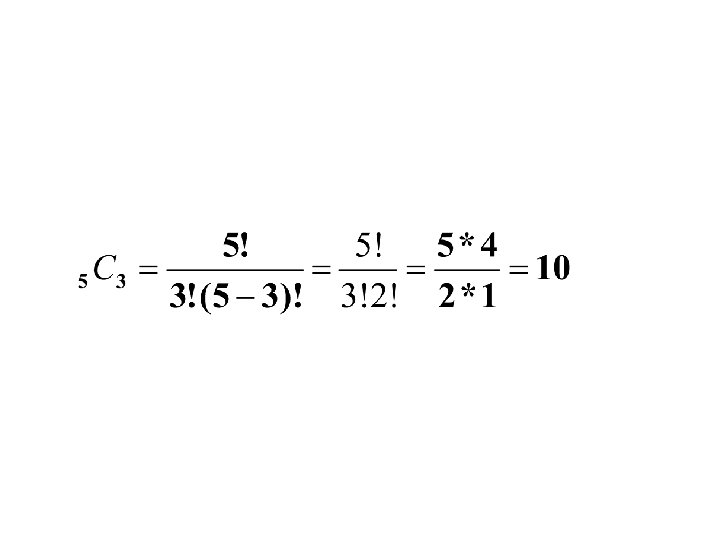










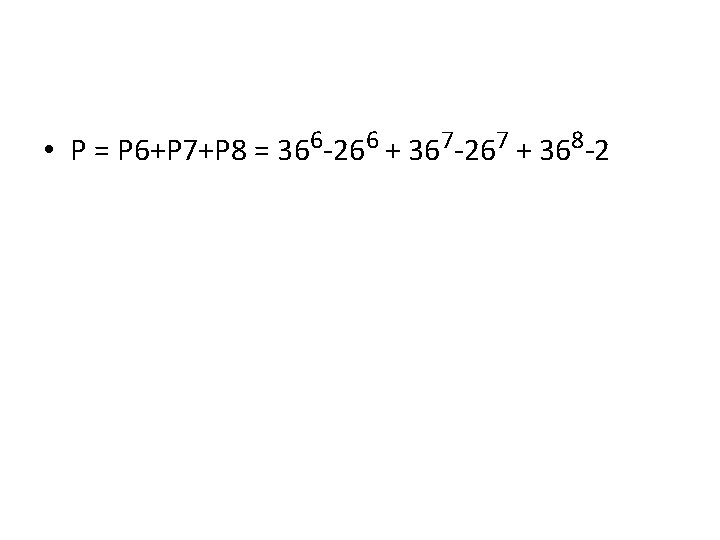



















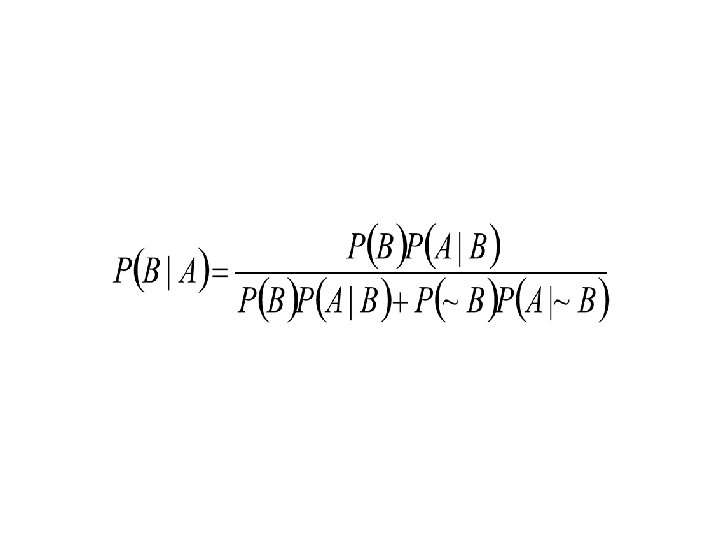







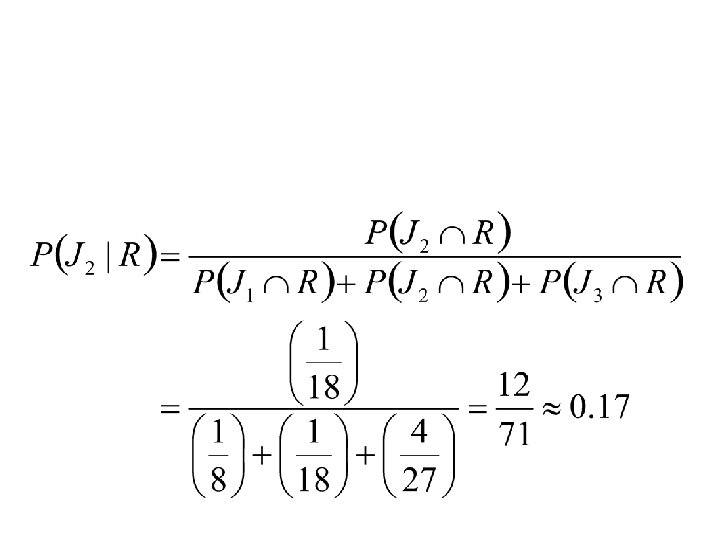
- Slides: 64

SE (Comp. Engg. ) Unit VI Discrete Structures Permutations and Combinations

• BOTH • PERMUTATIONS AND COMBINATIONS • USE A COUNTING METHOD CALLED FACTORIAL

• Lets start with a simple example. • A student is to roll a die and flip a coin. How many possible outcomes will there be?

• 1 H 2 H 3 H 4 H 5 H 6 H • 1 T 2 T 3 T 4 T 5 T 6 T

• The number of ways to arrange the letters ABC: ____ Number of choices for first blank? Number of choices for second blank? Number of choices for third blank? 3 ____ 3 2 1

Permutations • A Permutation is an arrangement of items in a particular order. The number of Permutations of n items chosen r at a time, is given by the formula

• Arrange 2 alphabets from a, b, c. • ab, ba, ac, ca, bc, cb • 3 P 2=3!/(3 -2)!=6

• A combination lock will open when the right choice of three numbers (from 1 to 30, inclusive) is selected. How many different lock combinations are possible assuming no number is repeated?
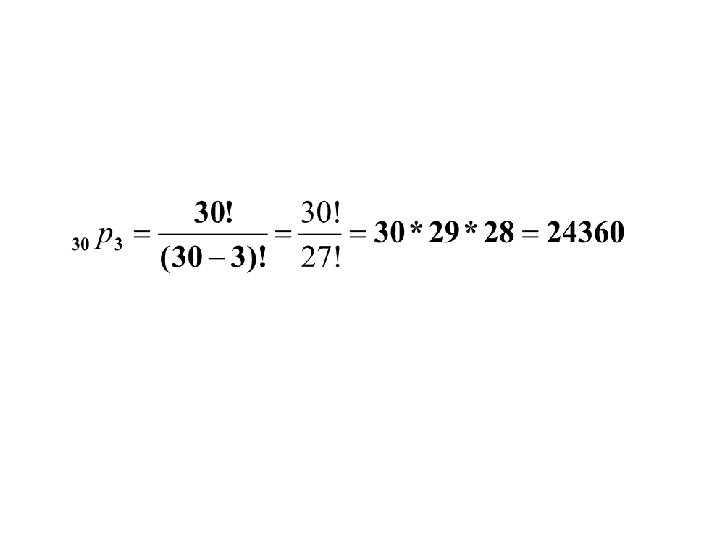

CIRCULAR PERMUTATIONS When items are in a circular format, to find the number of different arrangements, divide: n! / n

• Six students are sitting around a circular table in the cafeteria. How many different seating arrangements are there?

• 6! 6 = 120

Combination • A Combination is an arrangement of items in which order does not matter. The number of Combinations of n items chosen r at a time, is given by the formula

• To play a particular card game, each player is dealt five cards from a standard deck of 52 cards. How many different hands are possible?


• A student must answer 3 out of 5 essay questions on a test. In how many different ways can the student select the questions?
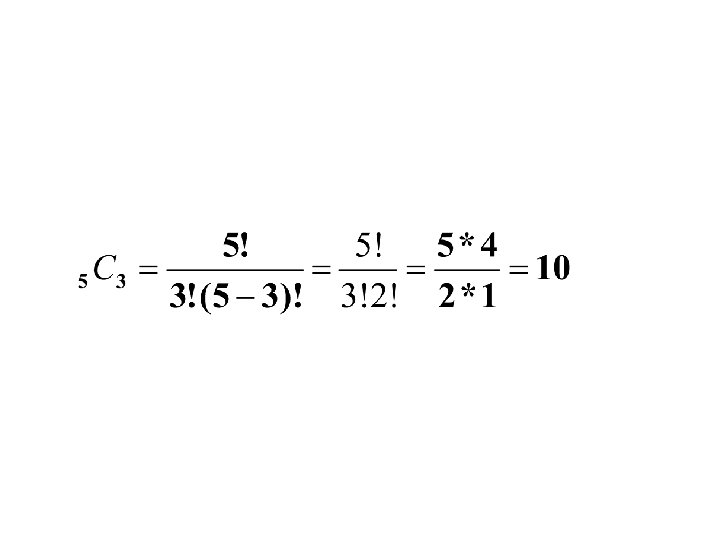

Product and Sum Rules • Product Rule: • If we need to perform procedure 1 AND procedure 2. There are n 1 ways to perform procedure 1 and n 2 ways to perform procedure 2. • There are n 1 • n 2 ways to perform procedure 1 AND procedure 2.

• Sum Rule: If need to perform either procedure 1 OR procedure 2. There are n 1 ways to perform procedure 1 and n 2 ways to perform procedure 2. • There are n 1+n 2 ways to perform procedure 1 OR procedure 2. • This “OR” is an “exclusive OR. ” One choice or the other, but not both.

• How many vehicle number plates can be made if each plate contains two different letters followed by three different digits

Two different letters are made in 26 P 2 ways. 3 different digits are combined in 10 P 3 ways Total no. of number plates= 26 P 2 * 10 P 3 =26!*10!/(24!*7!) =26*25*10*9*8 =468000

• An 8 member team is to be formed from a group of 10 men and 15 women. In how many ways can the team be chosen if : (i) The team must contain 4 men and 4 women (ii) There must be more men than women (iii) There must be at least two men

The team must contain 4 men and 4 women = 286650 (ii) There must be more men than women = (iii) There must be at least two men

• Passwords consist of character strings of 6 to 8 characters. Each character is an upper case letter or a digit. Each password must contain at least one digit. • How many passwords are possible?

• Total number is • # passwords with 6 char. + # passwords with 7 char. + # pws 8 char. • (=P 6+P 7+P 8).

• P 6: # possibilities without constraint : 366 • # exclusions is # passwords without any digits is 266 • And so, P 6 = 366 -266

• Similarly, P 7 = 367 -267 and P 8 = 368 -268
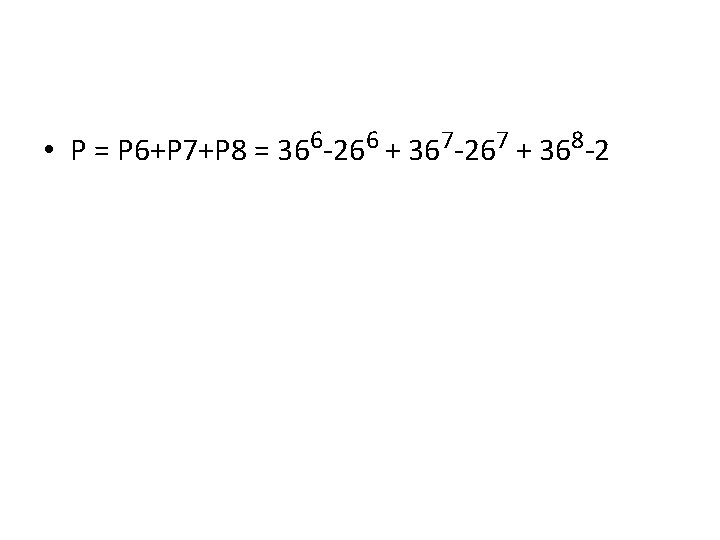
• P = P 6+P 7+P 8 = 366 -266 + 367 -267 + 368 -2
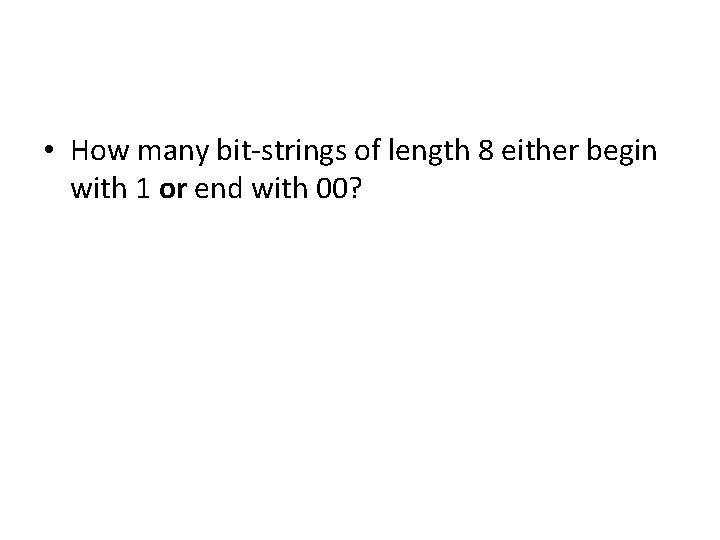
• How many bit-strings of length 8 either begin with 1 or end with 00?

• A = 8 -bit strings starting with 1 • |A| = # of 8 -bit strings starting with 1 is 27 • B = 8 -bit strings starting with 00 • |B| = # of 8 -bit strings ending with 00 is 26 • # of bit-strings begin with 1 and end with 00 is 25.

• # of 8 -bit strings starting with 1 or ending with 00 is • 27+ 2 6 - 2 5

• |A B| = |A| + |B| - |A B| • Inclusion–Exclusion Principle

Permutations with non-distinguishable objects • The number of different permutations of n objects, where there are non-distinguishable objects of type 1, non-distinguishable objects of type 2, …, and non-distinguishable objects of type k, is i. e. , C(n, )C(n- , )…C(n- - -…- , ) 33

• How many different strings can be made by reordering the letters of the word OFF

• • 3!/2!=3 OFF FFO FOF

• • • ONE OEN NEO NOE ENO EON

• How many different strings can be made by reordering the letters of the word SUCCESS

Generating Permutations Lexicographic method

• For the following 4 • combinations from the set f= {1; 2; 3; 4; 5; 6; 7} find the combination that immediately follows them in lexicographic order 1234 is followed by 3467 is followed by 4567 is followed by

What is probability? • Probability is the measure of how likely an event or outcome is. • Different events have different probabilities!

How do we describe probability? • You can describe the probability of an event with the following terms: – – certain (the event is definitely going to happen) likely (the event will probably happen, but not definitely) unlikely (the event will probably not happen, but it might) impossible (the event is definitely not going to happen)

• probabilities are expressed as fractions. – The numerator is the number of ways the event can occur. – The denominator is the number of possible events that could occur.

Random Experiment… • …a random experiment is an action or process that leads to one of several possible outcomes. For example: Experiment Outcomes Flip a coin Heads, Tails Exam Marks Numbers: 0, 1, 2, . . . , 100 Assembly Time t > 0 seconds Course Grades F, D, C, B, A, A+ 6. 43

What is the probability that I will choose a red marble? • In this bag of marbles, there are: – 3 red marbles – 2 white marbles – 1 purple marble – 4 green marbles

Probability example • Sample space: the set of all possible outcomes. • Probabilities: the likelihood of each of the possible outcomes (always 0 P 1. 0).

Probabilities… • List the outcomes of a random experiment… • This list must be exhaustive, i. e. ALL possible outcomes included. Die roll {1, 2, 3, 4, 5} Die roll {1, 2, 3, 4, 5, 6} • • The list must be mutually exclusive, i. e. no two outcomes can occur at the same time: Die roll {odd number or even number} Die roll{ number less than 4 or even number} 6. 46

• A and B are independent if and only if P(A&B)=P(A)*P(B) • A and B are mutually exclusive events: P(A or B) = P(A) + P(B)

Events & Probabilities… • The probability of an event is the sum of the probabilities of the simple events that constitute the event. • E. g. (assuming a fair die) S = {1, 2, 3, 4, 5, 6} and • P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = 1/6 • Then: • P(EVEN) = P(2) + P(4) + P(6) = 1/6 + 1/6 = 3/6 = 1/2 6. 48

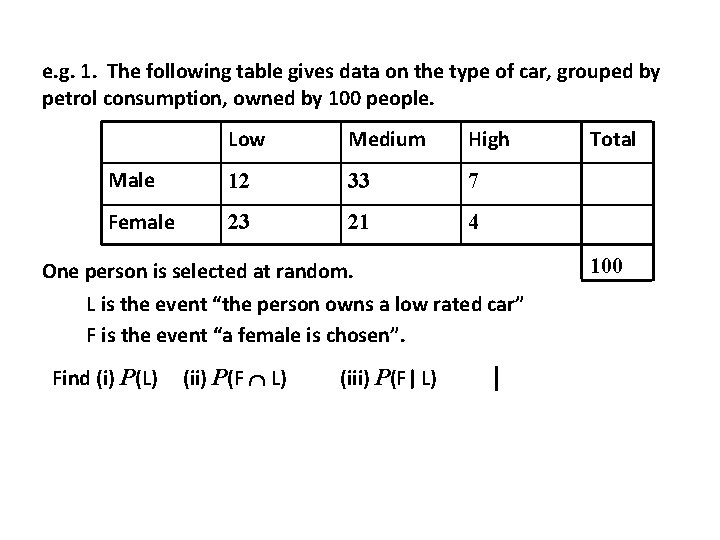
e. g. 1. The following table gives data on the type of car, grouped by petrol consumption, owned by 100 people. Low Medium High Male 12 33 7 Female 23 21 4 One person is selected at random. L is the event “the person owns a low rated car” F is the event “a female is chosen”. Find (i) P(L) (ii) P(F L) (iii) P(F| L) Total 100

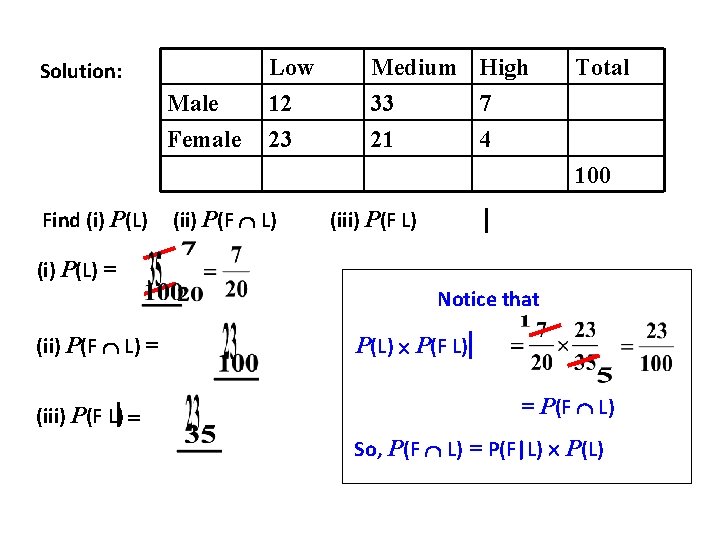
Solution: Male Female Low 12 23 Medium High 33 7 21 4 Total 100 Find (i) P(L) (ii) P(F L) (iii) P(F L) (i) P(L) = Notice that (ii) P(F L) = (iii) P(F L) = P(L) P(F L) = P(F L) So, P(F L) = P(F|L) P(L)

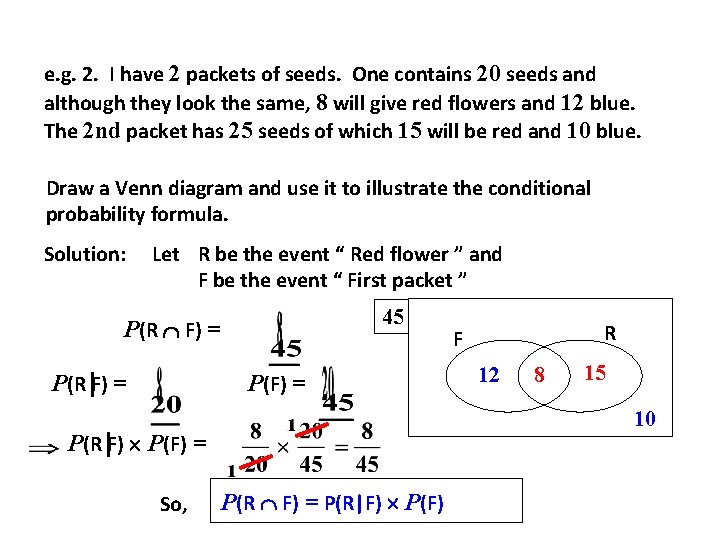
e. g. 2. I have 2 packets of seeds. One contains 20 seeds and although they look the same, 8 will give red flowers and 12 blue. The 2 nd packet has 25 seeds of which 15 will be red and 10 blue. Draw a Venn diagram and use it to illustrate the conditional probability formula. Solution: Let R be the event “ Red flower ” and F be the event “ First packet ” 45 P(R F) = P(R F) = P(F) = 12 8 15 10 P(R F) P(F) = So, R F P(R F) = P(R|F) P(F)

Bayes’ Rule: derivation • Definition: Let A and B be two events with P(B) 0. The conditional probability of A given B is:
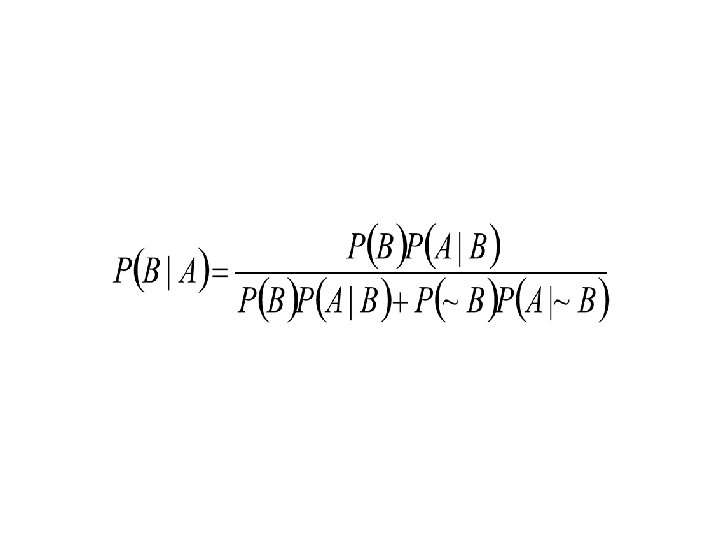

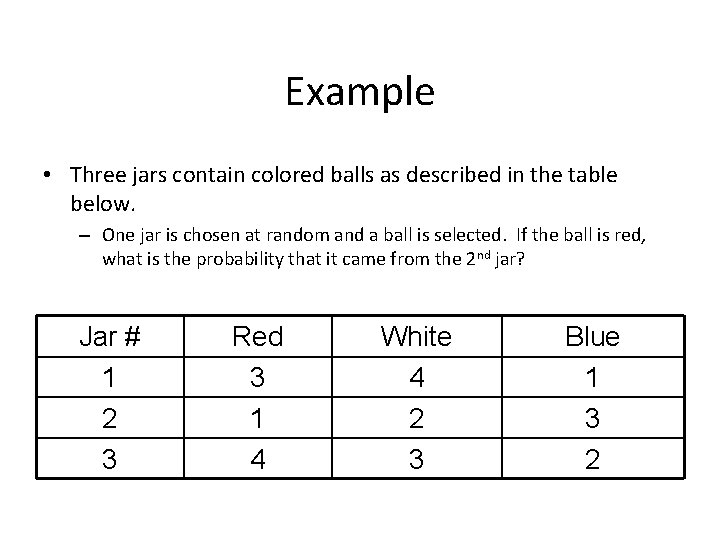
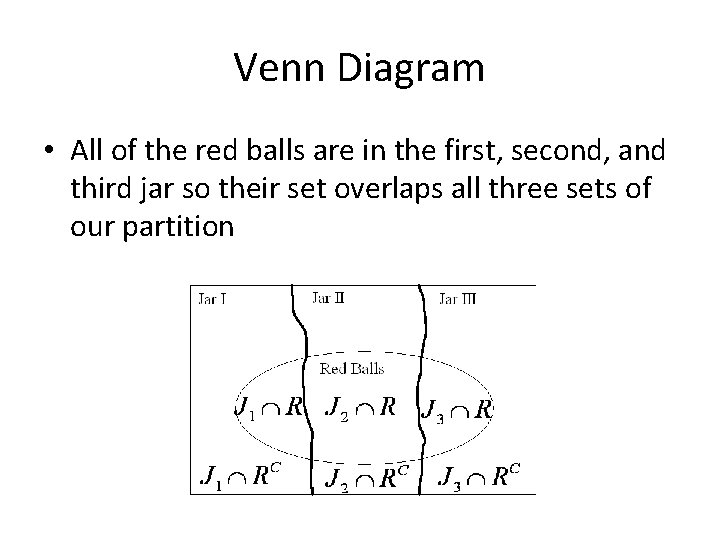
Example • Three jars contain colored balls as described in the table below. – One jar is chosen at random and a ball is selected. If the ball is red, what is the probability that it came from the 2 nd jar? Jar # 1 2 3 Red 3 1 4 White 4 2 3 Blue 1 3 2

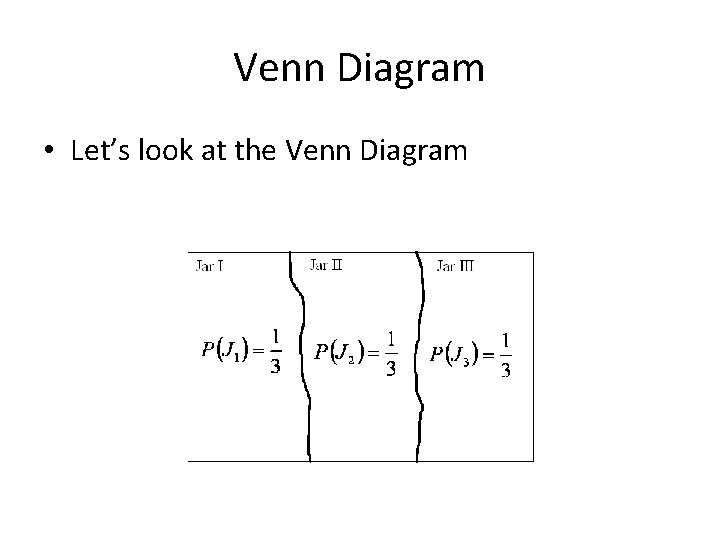
Example • We will define the following events: – J 1 is the event that first jar is chosen – J 2 is the event that second jar is chosen – J 3 is the event that third jar is chosen – R is the event that a red ball is selected

Example • The events J 1 , J 2 , and J 3 mutually exclusive – Why? • You can’t chose two different jars at the same time • Because of this, our sample space has been divided or partitioned along these three events

Venn Diagram • Let’s look at the Venn Diagram

Venn Diagram • All of the red balls are in the first, second, and third jar so their set overlaps all three sets of our partition

Finding Probabilities • What are the probabilities for each of the events in our sample space? • How do we find them?

Computing Probabilities • Similar calculations show:

Venn Diagram • Updating our Venn Diagram with these probabilities:

Where are we going with this? • Our original problem was: – One jar is chosen at random and a ball is selected. If the ball is red, what is the probability that it came from the 2 nd jar? • In terms of the events we’ve defined we want:

Finding our Probability
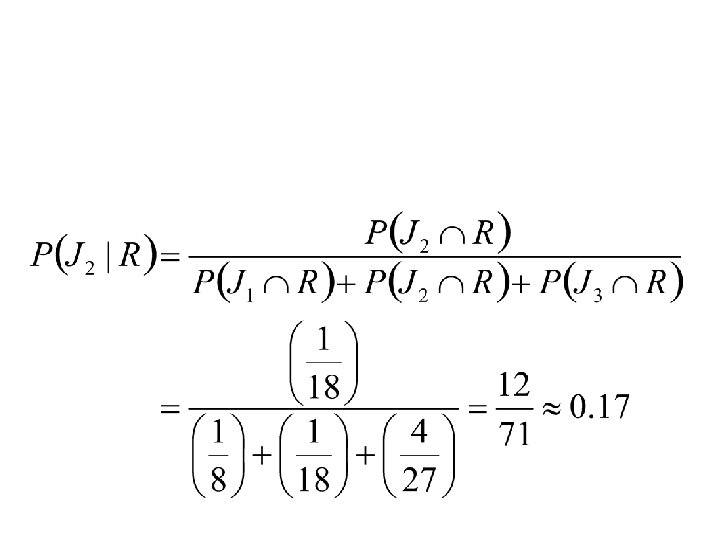
 Engg2780
Engg2780 Types of civil engineering
Types of civil engineering Engg 1100
Engg 1100 Engg 1100
Engg 1100 Unit 6 lesson 1 permutations and combinations
Unit 6 lesson 1 permutations and combinations Discrete structures
Discrete structures Discrete structures
Discrete structures What is discrete math
What is discrete math Discrete computational structures
Discrete computational structures Discrete structures
Discrete structures Cs 584
Cs 584 Discrete structures
Discrete structures Homology
Homology Permutation formula
Permutation formula Difference between permutations and combinations
Difference between permutations and combinations Combination example
Combination example Combination example
Combination example Permutation formula
Permutation formula What is 5 factorial
What is 5 factorial Permutations and combinations
Permutations and combinations Distinct permutations
Distinct permutations Permutations
Permutations Permutation with indistinguishable objects
Permutation with indistinguishable objects Permutation fundamental counting principle
Permutation fundamental counting principle Arrangements and permutations
Arrangements and permutations Number of rubik's cube permutations
Number of rubik's cube permutations Distinguishable permutations
Distinguishable permutations Permutation of multiset
Permutation of multiset Ncr formula
Ncr formula Counting rule for multiple-step experiment
Counting rule for multiple-step experiment Multiplication rule of counting
Multiplication rule of counting Lottery permutations
Lottery permutations Permutations probability
Permutations probability Permutations
Permutations Permutation
Permutation Combinations and permutations
Combinations and permutations How many bit strings of length 10 contain
How many bit strings of length 10 contain Circular permutation with restriction
Circular permutation with restriction Permutation group notation
Permutation group notation Georgia graduation test
Georgia graduation test Generalized permutations and combinations
Generalized permutations and combinations Generalized permutations and combinations
Generalized permutations and combinations Unit 10, unit 10 review tests, unit 10 general test
Unit 10, unit 10 review tests, unit 10 general test Unit 15 plant structures and taxonomy
Unit 15 plant structures and taxonomy Difference between primitive and non primitive data types
Difference between primitive and non primitive data types Doterra income disclosure
Doterra income disclosure Comp tox
Comp tox Apcsa recursion
Apcsa recursion Comp3007
Comp3007 Comp set hotel
Comp set hotel Hotel comp set benchmarking
Hotel comp set benchmarking Dairy comp 305 price
Dairy comp 305 price 1991105
1991105 External requirements in software engineering
External requirements in software engineering Im comp plan
Im comp plan Comp 4620
Comp 4620 Excel comp planning
Excel comp planning Cs110 northwestern
Cs110 northwestern David stotts unc
David stotts unc Comp sci 1102
Comp sci 1102 Comp 6321 concordia
Comp 6321 concordia Comp 585
Comp 585 Comp 553
Comp 553 Comp 512
Comp 512 Comp 512
Comp 512