Permutation Groups Part 1 Definition n A permutation

  • Slides: 22
Download presentation
Permutation Groups Part 1

Permutation Groups Part 1

Definition n A permutation of a set A is a function from A to

Definition n A permutation of a set A is a function from A to A that is both one to one and onto.

Array notation n n Let A = {1, 2, 3, 4} Here are two

Array notation n n Let A = {1, 2, 3, 4} Here are two permutations of A:

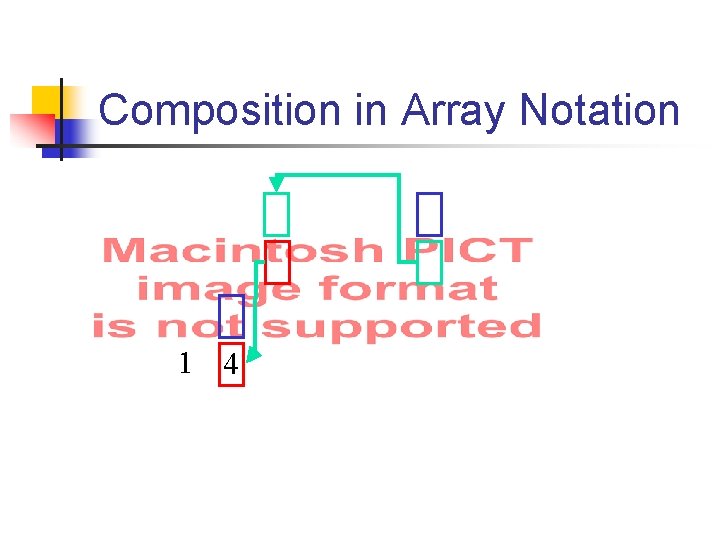
Composition in Array Notation 1

Composition in Array Notation 1

Composition in Array Notation 1 4

Composition in Array Notation 1 4

Composition in Array Notation 1 4 2

Composition in Array Notation 1 4 2

Composition in Array Notation 1 4 2 3

Composition in Array Notation 1 4 2 3

Composition in Array Notation 1 4 2 3

Composition in Array Notation 1 4 2 3

Definition n A permutation group of a set A is a set of permutations

Definition n A permutation group of a set A is a set of permutations of A that forms a group under function composition.

Example n n The set of all permutations on {1, 2, 3} is called

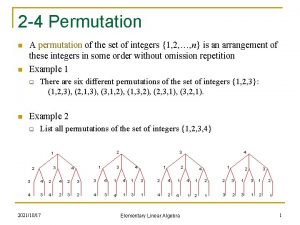
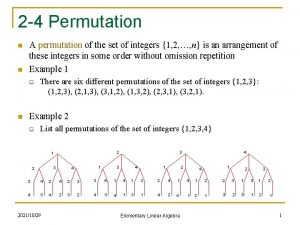
Example n n The set of all permutations on {1, 2, 3} is called the symmetric group on three letters, denoted S 3 There are 6 permutations possible:

S 3 n The permutations of {1, 2, 3}:

S 3 n The permutations of {1, 2, 3}:

Is S 3 a group? n n Composition of functions is always associative. Identity

Is S 3 a group? n n Composition of functions is always associative. Identity is . Since permutations are one to one and onto, there exist inverses (which are also permutations. Therefore, S 3 is group.

Computations in S 3

Computations in S 3

Simplified computations in S 3 Double the exponent of when switching with . You

Simplified computations in S 3 Double the exponent of when switching with . You can simplify any expression in S 3! n

Symmetric groups, Sn n Let A = {1, 2, … n}. The symmetric group

Symmetric groups, Sn n Let A = {1, 2, … n}. The symmetric group on n letters, denoted Sn, is the group of all permutations of A under composition. Sn is a group for the same reasons that S 3 is group. |Sn| = n!

Symmetries of a square, D 4 3 2 4 1 D 4 ≤ S

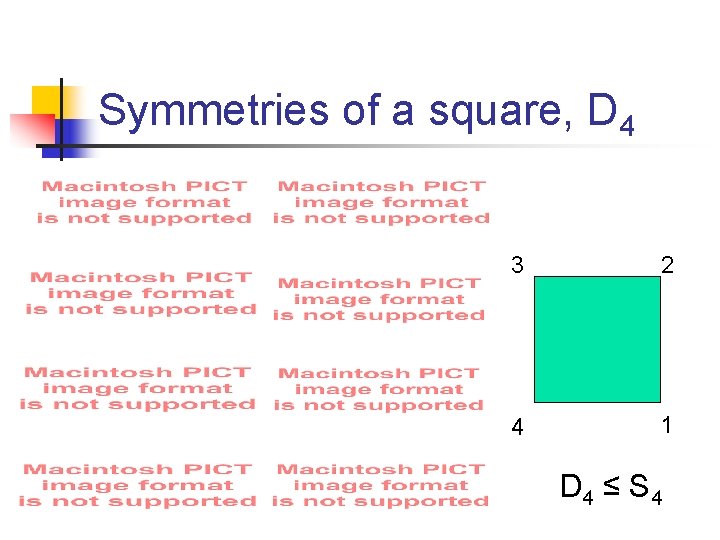
Symmetries of a square, D 4 3 2 4 1 D 4 ≤ S 4

Why do we care? n Every group turns out to be a permutation group

Why do we care? n Every group turns out to be a permutation group on some set! (To be proved later).

Cycle Notation

Cycle Notation

Disjoint cycles n n Two permutations are disjoint if the sets of elements moved

Disjoint cycles n n Two permutations are disjoint if the sets of elements moved by the permutations are disjoint. Every permutation can be represented as a product of disjoint cycles.

Algorithm for disjoint cycles n n n Let permutation π be given. Let a

Algorithm for disjoint cycles n n n Let permutation π be given. Let a be the identity permutation, represented by an empty list of cycles. while there exists n with π(n) ≠ a(n): start a new cycle with n let b = n while

Compostion in cycle notation n n = (1 2 3)(1 2)(3 4) = (1

Compostion in cycle notation n n = (1 2 3)(1 2)(3 4) = (1 3 4)(2) = (1 3 4) = (1 2)(3 4)(1 2 3) = (1)(2 4 3) = (2 4 3)

Compostion in cycle notation n n = (1 2 3)(1 2)(3 4) = (1

Compostion in cycle notation n n = (1 2 3)(1 2)(3 4) = (1 1 1 2 3 = (1 2)(3 4)(1 2 3)

Permutation Groups Definitions A Permutation of a setPermutation Groups Definitions A Permutation of a set
PERMUTATION DEFINITION A permutation is an arrangement inPERMUTATION DEFINITION A permutation is an arrangement in
6 3 Permutation groups and cyclic groups Example6 3 Permutation groups and cyclic groups Example
Chapter 15 Permutation Combination 1152020 Permutation and combinationChapter 15 Permutation Combination 1152020 Permutation and combination
Permutation A permutation is an arrangement in whichPermutation A permutation is an arrangement in which
Algorithmic Graph Theory Permutation Graphs Permutation Labeling 2Algorithmic Graph Theory Permutation Graphs Permutation Labeling 2
Chapter 15 Permutation Combination 6162021 Permutation and combinationChapter 15 Permutation Combination 6162021 Permutation and combination
2 4 Permutation n n A permutation of2 4 Permutation n n A permutation of
Chapter 34 Permutation Combination 10202021 Permutation and combinationChapter 34 Permutation Combination 10202021 Permutation and combination
2 4 Permutation n n A permutation of2 4 Permutation n n A permutation of
DETERMINANT MATH 80 Linear Algebra PERMUTATION PERMUTATION INVERSIONDETERMINANT MATH 80 Linear Algebra PERMUTATION PERMUTATION INVERSION
SECTION 8 Groups of Permutations Definition A permutationSECTION 8 Groups of Permutations Definition A permutation
SAFETY GROUPS JEOPARDY Safety Groups Program Safety GroupsSAFETY GROUPS JEOPARDY Safety Groups Program Safety Groups
Chapter 6 Social Groups and Societies Groups GroupsChapter 6 Social Groups and Societies Groups Groups
Functional Groups Functional groups special groups of atomsFunctional Groups Functional groups special groups of atoms
Interest Groups Interest Groups Key Concepts Interest groupsInterest Groups Interest Groups Key Concepts Interest groups
Pressure Groups What are Pressure Groups Pressure groupsPressure Groups What are Pressure Groups Pressure groups
Interest Groups How Interest Groups Work Interest GroupsInterest Groups How Interest Groups Work Interest Groups
Groups vs Teams Groups l Groups are aGroups vs Teams Groups l Groups are a
Interest Groups Chapter 7 Interest Groups Interest groupsInterest Groups Chapter 7 Interest Groups Interest groups
Peer Groups Cliques Adolescent Groups versus Childrens GroupsPeer Groups Cliques Adolescent Groups versus Childrens Groups