School of Mechanical Engineering Tel Aviv University Israel

School of Mechanical Engineering, Tel Aviv University, Israel Combinatorial synthesis and singularities of Assur graphs, BKC and parallel mechanisms Prof. Offer Shai

• • • Outline Body-Bar and Body – Hinge Graphs Directed Graphs, Cut-sets and strongly connected graphs Baranov Trusses & Assur Graphs as Body-Hinge Basic Kinematic Chains as Body-Hinge Kennedy Theorem & the Coupling Degree The coupling degree of Bar-joint AGs (theorem) and BKCs (BB AGs) (conjecture) Combinatorial Synthesis Algorithm for mechanisms (Hahn & Shai, 2015) Singularity Characterization through dual Kennedy Singularity Characterization of Baranov Truss (Sheffer & Shai, 2015) The dual Baranov coupling degree conjecture Planetary gear trains of BKC and their coupling degree.

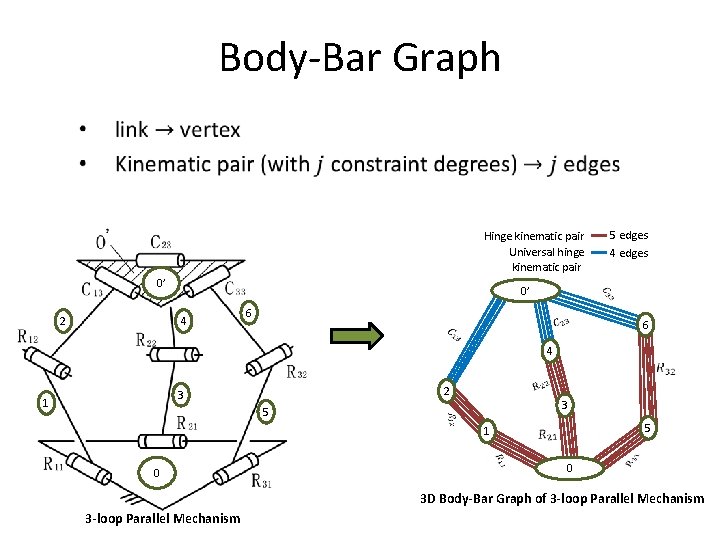
Body-Bar Graph Hinge kinematic pair Universal hinge kinematic pair 0’ 2 5 edges 4 edges 0’ 4 6 6 4 2 3 1 3 5 5 1 0 0 3 D Body-Bar Graph of 3 -loop Parallel Mechanism

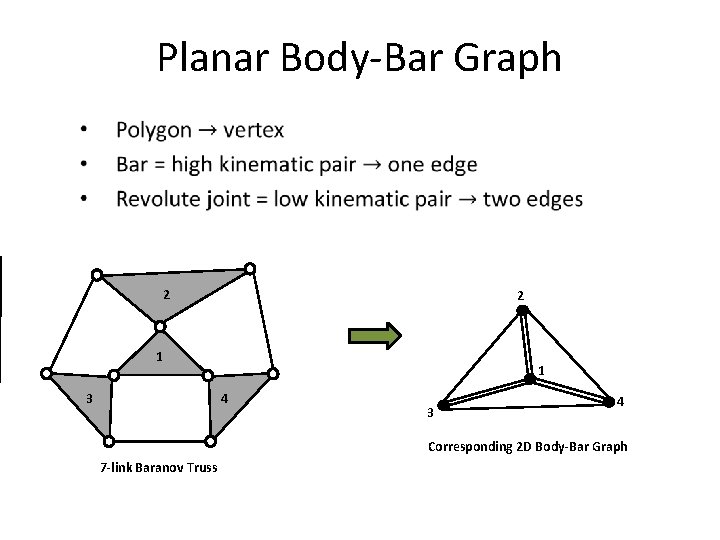
Planar Body-Bar Graph 2 2 1 1 4 3 3 4 Corresponding 2 D Body-Bar Graph 7 -link Baranov Truss

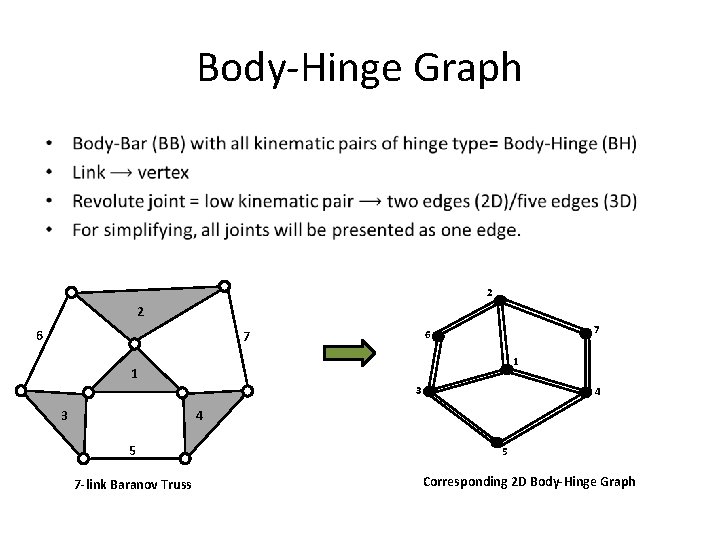
Body hinge graphs • Correspond to mechanisms that have only lower kinematic pairs (revolute joints), in 3 D only hinges. • We will see how to transform Body bar graphs (BKC) into body hinge graphs and vice versa.

Body-Hinge Graph • 2 2 6 7 1 1 3 4 4 3 5 7 -link Baranov Truss 5 Corresponding 2 D Body-Hinge Graph

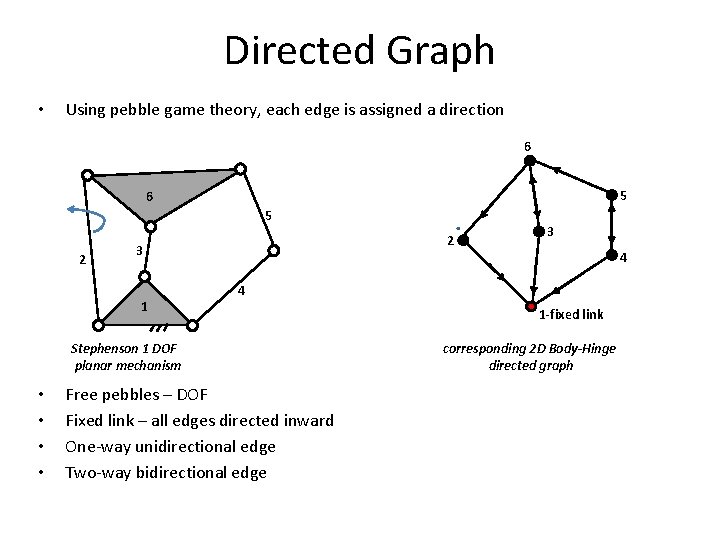
Directed Graph • Using pebble game theory, each edge is assigned a direction 6 5 2 2 3 1 3 4 4 Stephenson 1 DOF planar mechanism • • . Free pebbles – DOF Fixed link – all edges directed inward One-way unidirectional edge Two-way bidirectional edge 1 -fixed link corresponding 2 D Body-Hinge directed graph

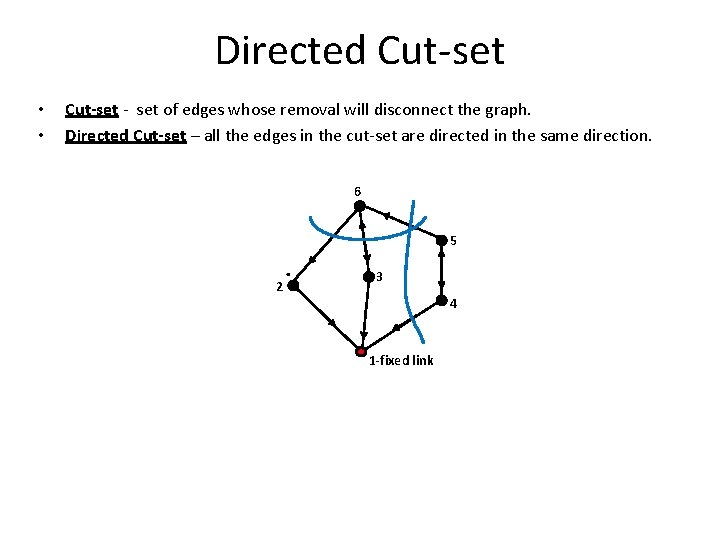
Directed Cut-set • • Cut-set - set of edges whose removal will disconnect the graph. Directed Cut-set – all the edges in the cut-set are directed in the same direction. 6 5 2 . 3 4 1 -fixed link

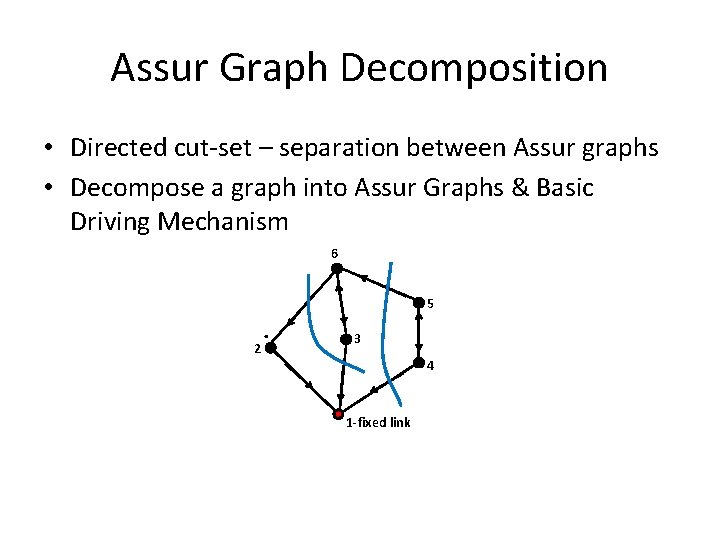
Assur Graph Decomposition • Directed cut-set – separation between Assur graphs • Decompose a graph into Assur Graphs & Basic Driving Mechanism 6 5 2 . 3 4 1 -fixed link

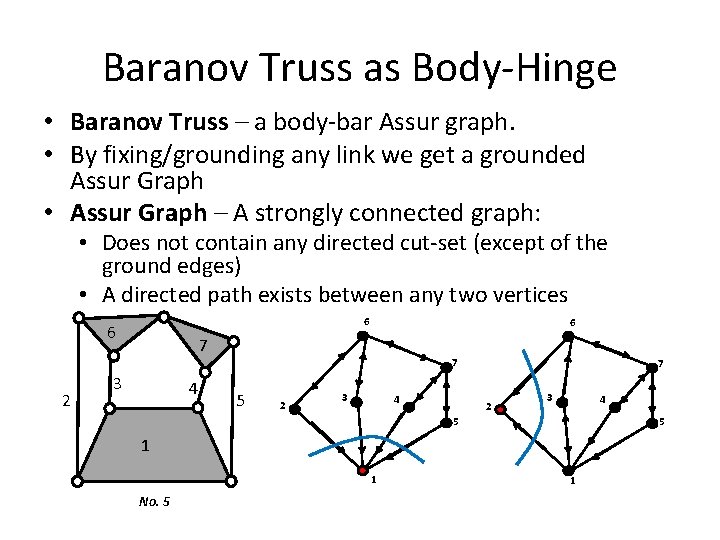
Baranov Truss as Body-Hinge • Baranov Truss – a body-bar Assur graph. • By fixing/grounding any link we get a grounded Assur Graph • Assur Graph – A strongly connected graph: • Does not contain any directed cut-set (except of the ground edges) • A directed path exists between any two vertices 6 6 6 7 7 2 3 4 5 2 3 4 7 2 3 4 5 5 1 1 No. 5 1

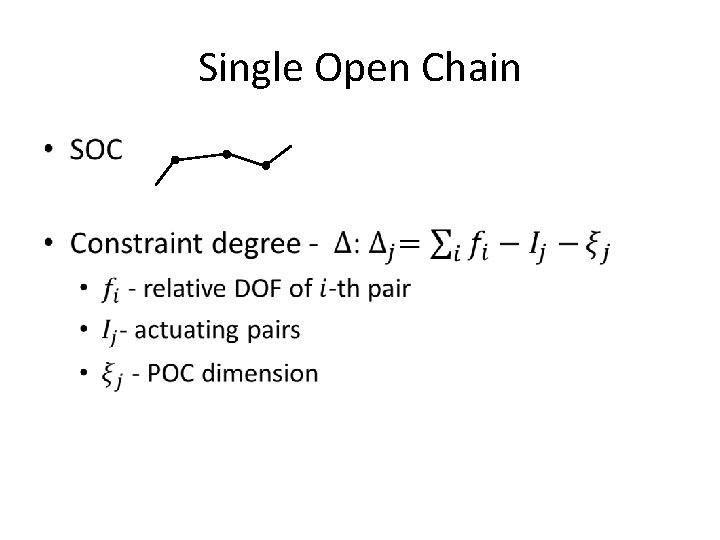
Single Open Chain •

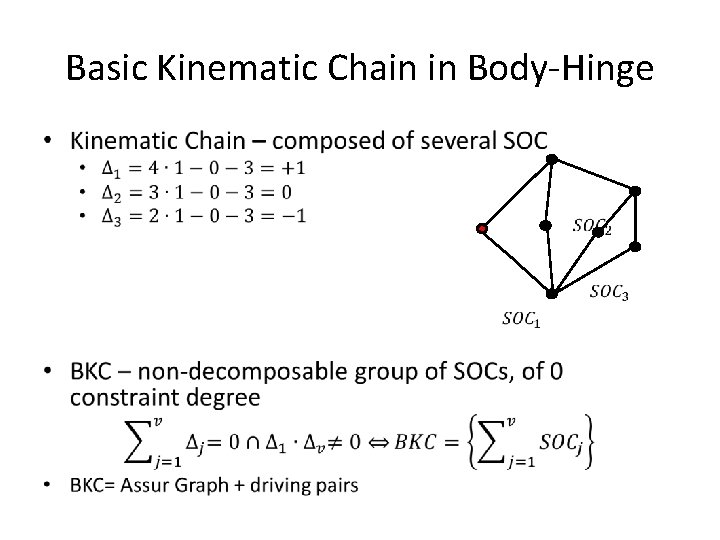
Basic Kinematic Chain in Body-Hinge •

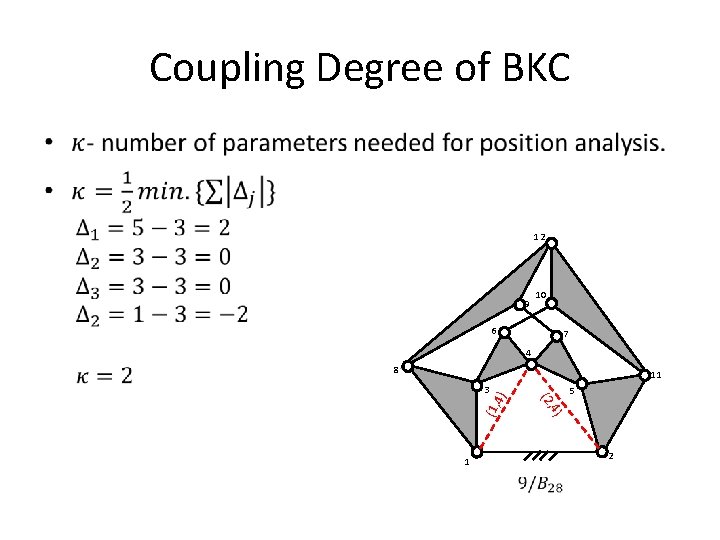
Coupling Degree of BKC • 12 9 10 6 7 4 8 5 , 4) 1 (2 (1, 4 3 ) 11 2

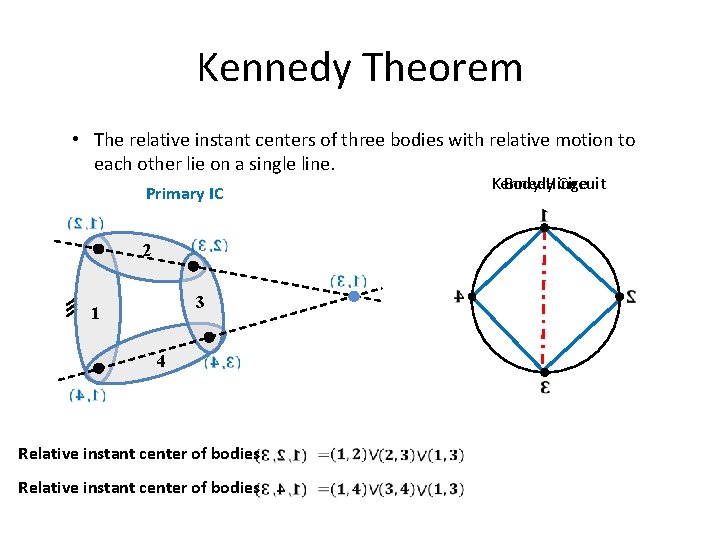
Kennedy Theorem • The relative instant centers of three bodies with relative motion to each other lie on a single line. Primary IC 2 3 1 4 Relative instant center of bodies Body-Hinge Kennedy Circuit

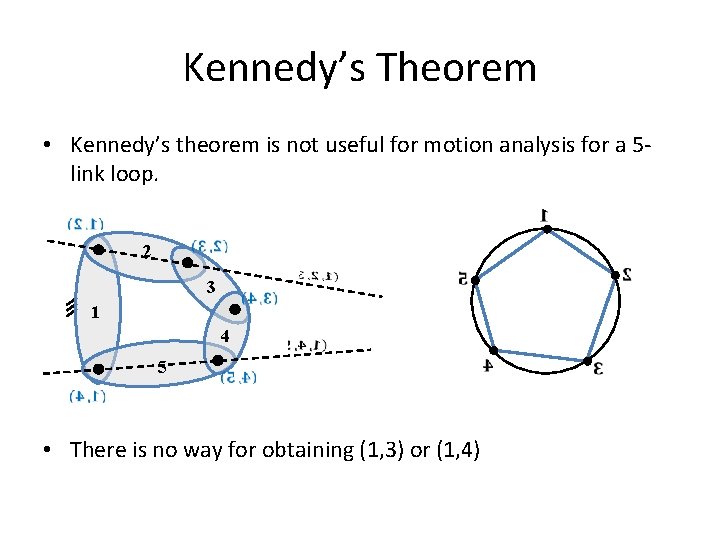
Kennedy’s Theorem • Kennedy’s theorem is not useful for motion analysis for a 5 link loop. 2 3 1 4 5 • There is no way for obtaining (1, 3) or (1, 4)

Kennedy’s Method • By finding the IC of all links relative to the fixed link, position (motion) analysis of all links is obtainable. (if all the ICs are found then the analysis of the system is obtainable). • A kinematic chain which can be analyzed using Kennedy’s theorem is a simple kinematic chain. • A kinematic chain which cannot be analyzed using Kennedy’s theorem is a complex kinematic chain.

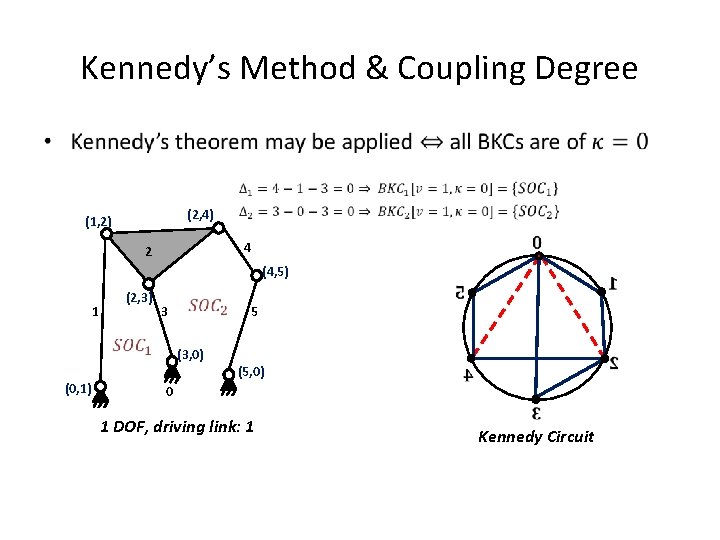
Kennedy’s Method & Coupling Degree • (2, 4) (1, 2) 4 2 (4, 5) 1 (2, 3) 3 5 (3, 0) (0, 1) (5, 0) 0 1 DOF, driving link: 1 Kennedy Circuit

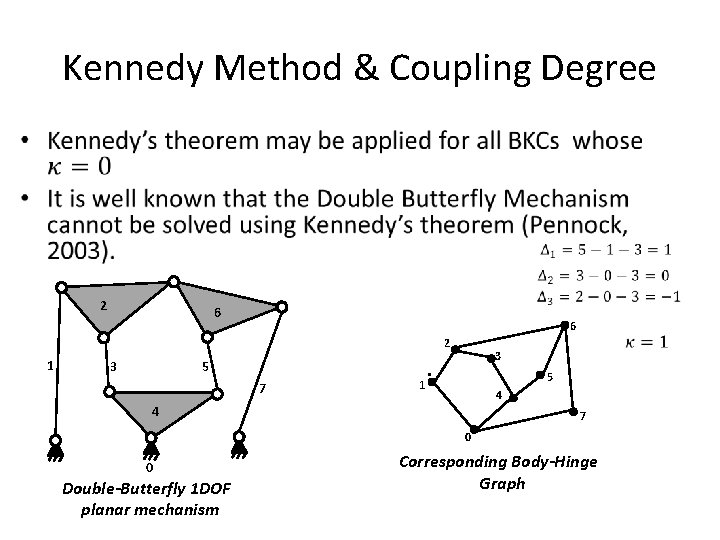
Kennedy Method & Coupling Degree • 2 6 6 2 1 3 5 7 1 3 . 5 4 4 7 0 0 Double-Butterfly 1 DOF planar mechanism Corresponding Body-Hinge Graph

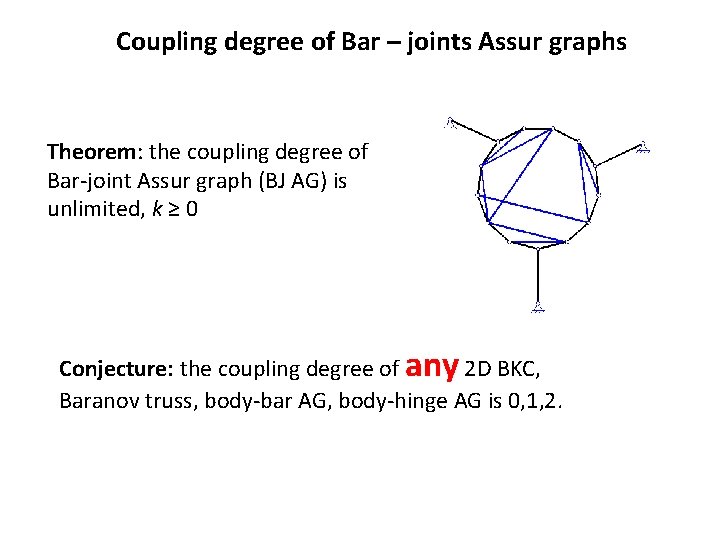
Coupling degree of Bar – joints Assur graphs Theorem: the coupling degree of Bar-joint Assur graph (BJ AG) is unlimited, k ≥ 0 Conjecture: the coupling degree of any 2 D BKC, Baranov truss, body-bar AG, body-hinge AG is 0, 1, 2.

Combinatorial Synthesis Algorithm (Hahn & Shai, 2015) • Using Graph Theory (directed graphs). • A relation occurs between the number and type of initiations, and of the coupling degree. • The algorithm will attempt to find Assur Graphs: o all graphs in 2 D: Body-Hinge (Baranov Truss), Body-Bar, Bar & Joint o some Assur Graphs in 3 D

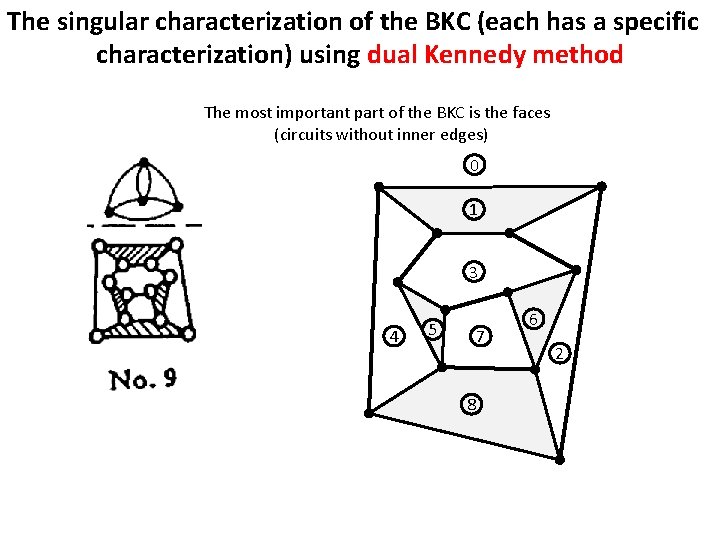
The singular characterization of the BKC (each has a specific characterization) using dual Kennedy method The most important part of the BKC is the faces (circuits without inner edges) 0 1 3 4 5 7 8 6 2

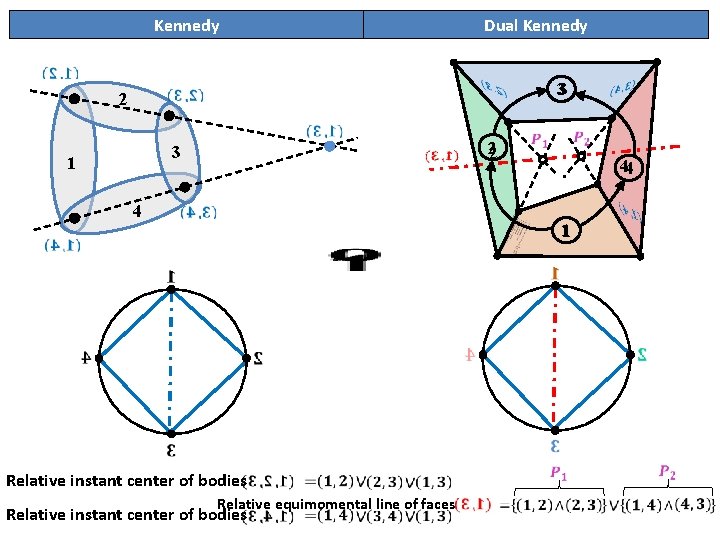
Kennedy Dual Kennedy 33 2 22 3 1 4 44 1 Relative instant center of bodies Relative equimomental line of faces Relative instant center of bodies

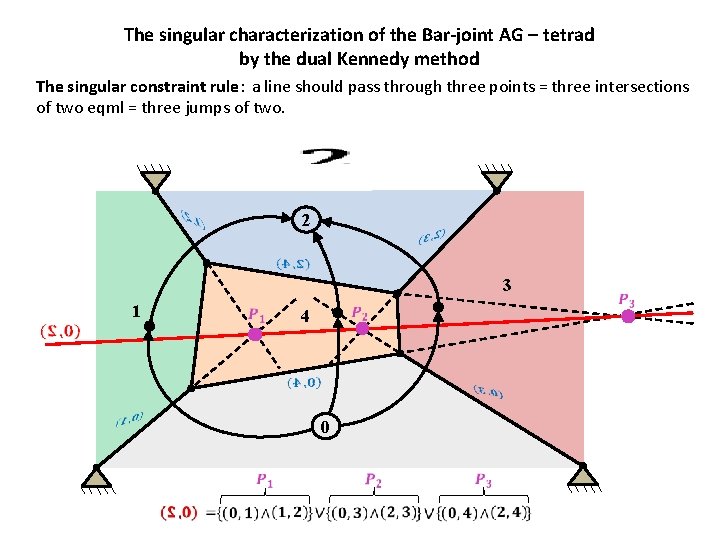
The singular characterization of the Bar-joint AG – tetrad by the dual Kennedy method The singular constraint rule: a line should pass through three points = three intersections of two eqml = three jumps of two. 2 3 1 4 0

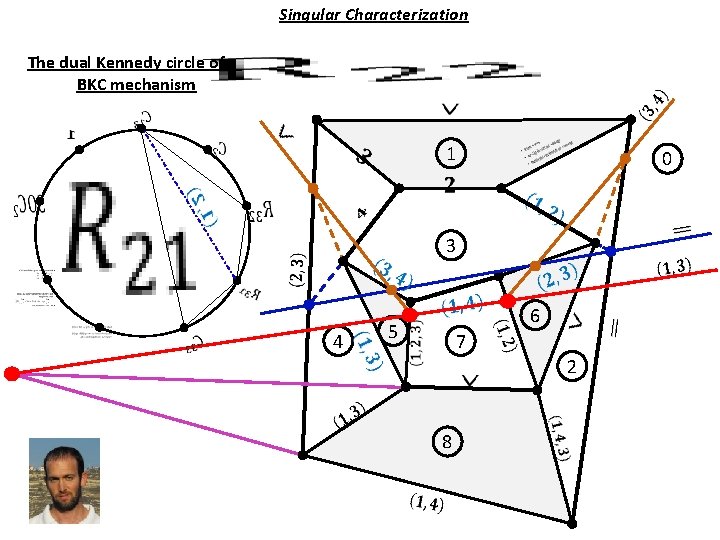
Singular Characterization The dual Kennedy circle of a BKC mechanism 1 0 3 4 6 5 7 2 8

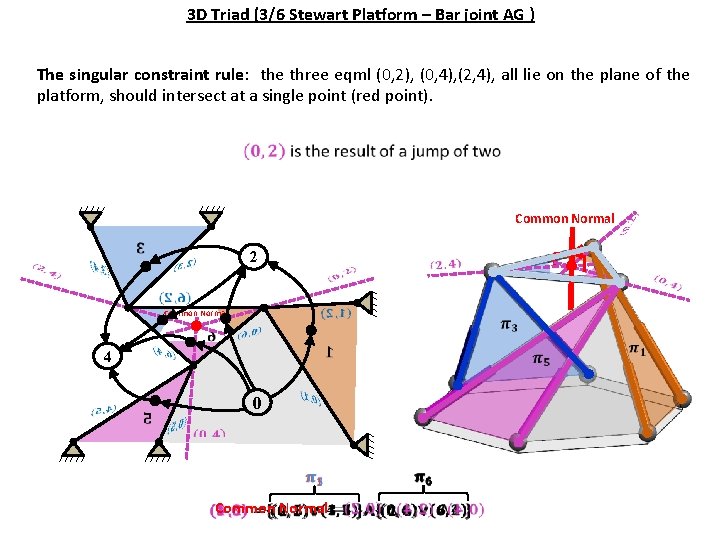
3 D Triad (3/6 Stewart Platform – Bar joint AG ) The singular constraint rule: the three eqml (0, 2), (0, 4), (2, 4), all lie on the plane of the platform, should intersect at a single point (red point). Common Normal 2 Common Normal 4 0 Common Normal

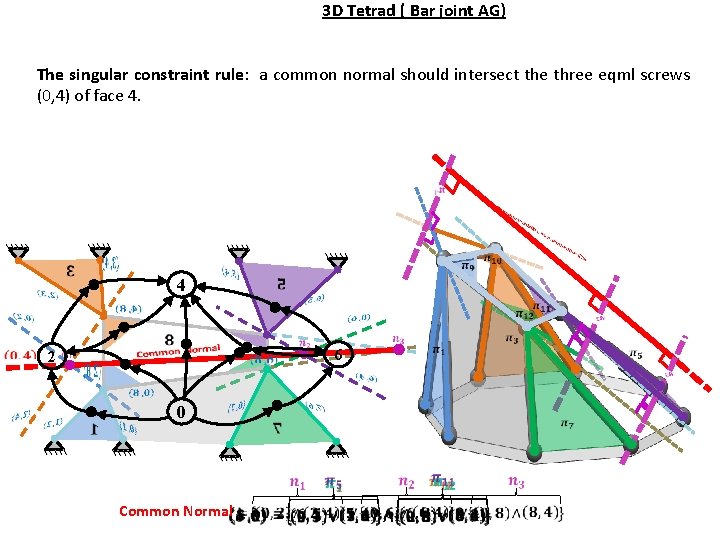
3 D Tetrad ( Bar joint AG) The singular constraint rule: a common normal should intersect the three eqml screws (0, 4) of face 4. 4 6 2 0 Common Normal

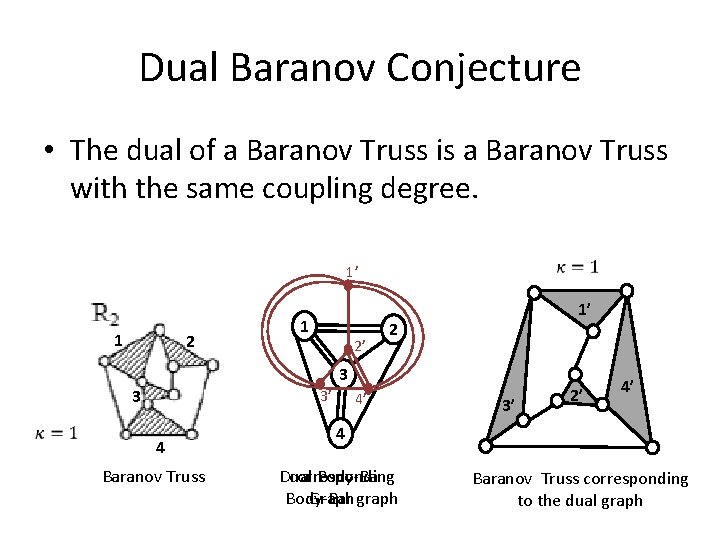
Dual Baranov Conjecture • The dual of a Baranov Truss is a Baranov Truss with the same coupling degree. 1’ 1 2’ 1’ 2 3 3 3’ 4 Baranov Truss 4’ 3’ 2’ 4’ 4 corresponding Dual Body-Bar Graph graph Baranov Truss corresponding to the dual graph

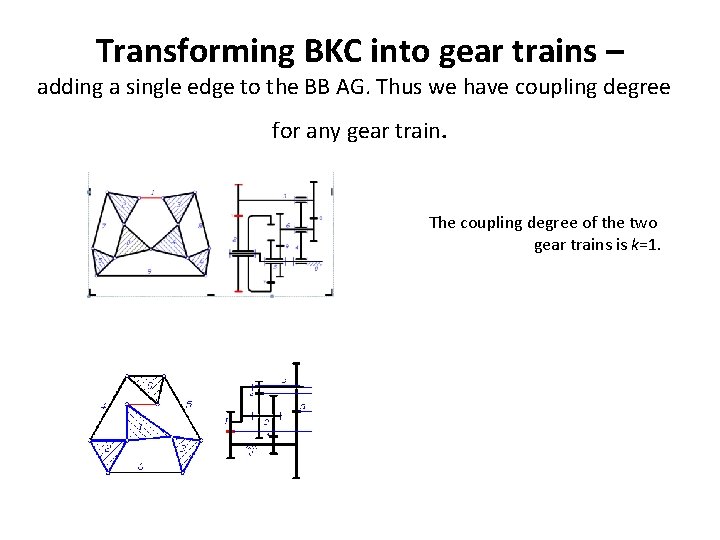
Transforming BKC into gear trains – adding a single edge to the BB AG. Thus we have coupling degree for any gear train. The coupling degree of the two gear trains is k=1.

Thank You For Watching!