Rozklad mnoholen na souin Opakovn znalost o vrazech

Rozklad mnohočlenů na součin Opakování znalostí o výrazech Odvození rozkladných vzorců (vzorců pro rozklad výrazů na součin) Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Radomír Macháň. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.

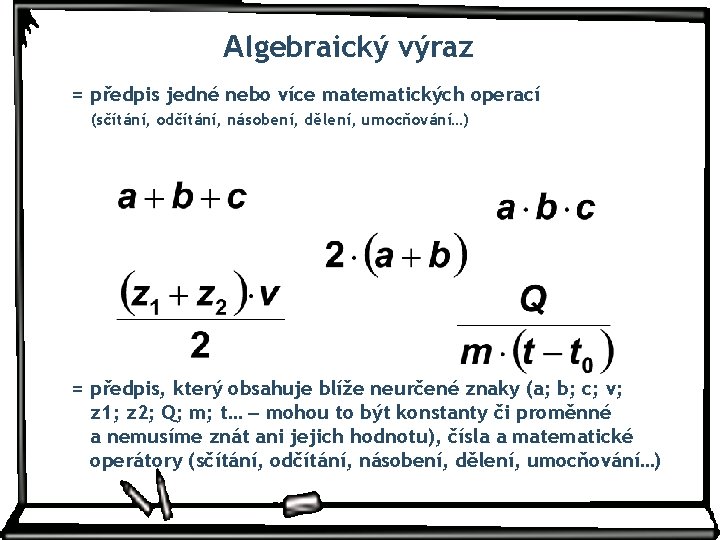
Algebraický výraz = předpis jedné nebo více matematických operací (sčítání, odčítání, násobení, dělení, umocňování…) = předpis, který obsahuje blíže neurčené znaky (a; b; c; v; z 1; z 2; Q; m; t… – mohou to být konstanty či proměnné a nemusíme znát ani jejich hodnotu), čísla a matematické operátory (sčítání, odčítání, násobení, dělení, umocňování…)

Číselný a algebraický výraz Existují dva druhy výrazů podle toho, z čeho jsou sestaveny: 1) Výrazy, v nichž se vyskytují jenom čísla: Číselné výrazy 7 : (6 – 3. 2) – 2. 3 5. (4 – 3) – 6 : 3 4. 2, 5 – 6 + 22 2) Výrazy, v nichž se vyskytují proměnné, které zastupují čísla z určité množiny: Algebraické výrazy x – 6 + 3 x (x + 2) / 4 y 2 – 6 y + 9

Mnohočleny Mnohočlen = zvláštní typ výrazů Mnohočleny obsahují pouze přirozené (jedné nebo více). mocniny neznámých … Mnohočlen s jednou proměnnou … Mnohočlen dvou proměnných … Není mnohočlen (x je ve jmenovateli, tzn. záporná mocnina x) … Není mnohočlen (obsahuje odmocninu z x, tzn. mocnina ve tvaru zlomku) … Je mnohočlen (sice obsahuje zlomek, ale bez neznámé ve jmenovateli)

Sčítání mnohočlenů Sčítat můžeme jen stejné členy se stejnou proměnnou a se stejným mocnitelem. To znamená čísla jen s čísly, proměnné jen s proměnnými, proměnné na druhou jen s proměnnými na druhou atd. 3+4=7 3 x 2 + 4 x 2 = 7 x 2 3 x + 4 x = 7 x Příklad: (3 x 2 + 7 x – 5) + (-2 x 2 – 4 x + 1) = 3 x 2 + 7 x – 5 – 2 x 2 – 4 x + 1 = = 3 x 2 – 2 x 2 + 7 x – 4 x – 5+1 = x 2 + 3 x – 4

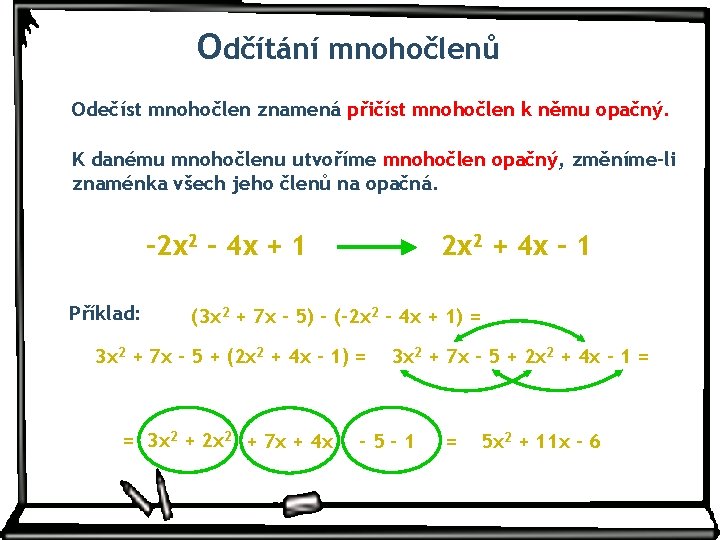
Odčítání mnohočlenů Odečíst mnohočlen znamená přičíst mnohočlen k němu opačný. K danému mnohočlenu utvoříme mnohočlen opačný, změníme-li znaménka všech jeho členů na opačná. – 2 x 2 – 4 x + 1 Příklad: 2 x 2 + 4 x – 1 (3 x 2 + 7 x – 5) - (-2 x 2 – 4 x + 1) = 3 x 2 + 7 x – 5 + (2 x 2 + 4 x – 1) = = 3 x 2 + 2 x 2 + 7 x + 4 x 3 x 2 + 7 x – 5 + 2 x 2 + 4 x – 1 = – 5 -1 = 5 x 2 + 11 x – 6

Násobení mnohočlenů Každý člen prvního mnohočlenu násobíme s každým členem druhého mnohočlenu a výsledné členy pak sečteme. (2 x – 1)(2 x 2 – 4 x + 1) = = 4 x 3 - 8 x 2 + 2 x - 2 x 2 + 4 x - 1 Příklad: (3 x 2 + 7 x – 5). (-2 x 2 – 4 x + 1) = = -6 x 4 - 12 x 3 + 3 x 2 - 14 x 3 - 28 x 2 + 7 x + 10 x 2 + 20 x - 5 = = -6 x 4 - 12 x 3 - 14 x 3 + 3 x 2 - 28 x 2 + 10 x 2 + 7 x + 20 x - 5 = = -6 x 4 - 26 x 3 - 15 x 2 + 27 x - 5

Rozklad mnohočlenu na součin Obdobně jako v případě počítání s číselnými výrazy (zlomky), můžeme i v případě lomených výrazů s proměnnou, za dodržení podmínek krácení (tj. dělíme čitatele i jmenovatele stejným číslem, výrazem, mnohočlenem různým od nuly), krátit výrazy (mnohočleny) nad sebou a v případě součinu i do kříže. Proto se naučíme rozkládat mnohočleny na součin.

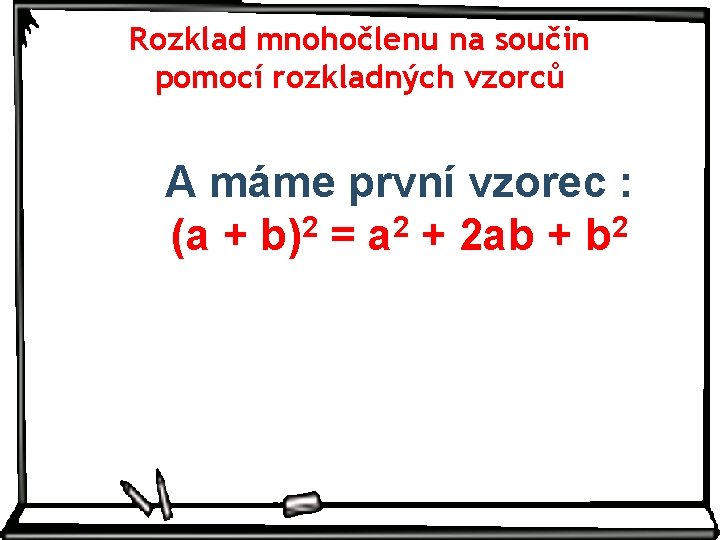
Rozklad mnohočlenu na součin pomocí rozkladných vzorců Na základě našich znalostí si vzorce odvodíme Uprav daný výraz umocněním závorky: Tak ještě jednou obecněji:

Rozklad mnohočlenu na součin pomocí rozkladných vzorců A máme první vzorec : (a + b)2 = a 2 + 2 ab + b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a + b)2 = a 2 + 2 ab + b 2 Uprav daný výraz již jen pomocí vzorce: a b a 2 + 2 ab + b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a + b)2 = a 2 + 2 ab + b 2 Uprav daný výraz již jen pomocí vzorce: a b a 2 + 2 ab + b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a + b)2 = a 2 + 2 ab + b 2 Uprav daný výraz již jen pomocí vzorce: a b a 2 + 2 ab + b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Uprav daný výraz umocněním závorky: Tak ještě jednou obecněji:

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Druhý vzorec : (a - b)2 = a 2 - 2 ab + b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a – b)2 = a 2 – 2 ab + b 2 Uprav daný výraz již jen pomocí vzorce: a b a 2 – 2 ab + b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a – b)2 = a 2 – 2 ab + b 2 Uprav daný výraz již jen pomocí vzorce: a b a 2 – 2 ab + b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a – b)2 = a 2 – 2 ab + b 2 Uprav daný výraz již jen pomocí vzorce: a b a 2 – 2 ab + b 2

Rozklad mnohočlenu na součin pomocí rozkladných vzorců A ještě jeden vzorec. Uprav: Tak ještě jednou obecněji:

Rozklad mnohočlenu na součin pomocí rozkladných vzorců Třetí vzorec tedy je: (a + b). (a – b) = a 2 – b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a + b). (a – b) = a 2 – b 2 Uprav daný výraz již jen pomocí vzorce: a + b a a 2 – b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a + b). (a – b) = a 2 – b 2 Uprav daný výraz již jen pomocí vzorce: a + b a – b a 2 – b 2

Rozklad mnohočlenu na součin – pomocí rozkladných vzorců Příklady na ujasnění: (a + b). (a – b) = a 2 – b 2 Uprav daný výraz již jen pomocí vzorce: a a b + a 2 – b

Rozkladné vzorce Všechny tři vzorce však budeme mnohem častěji používat obráceně, tzn. tak, abychom pomocí nich rozkládali dané mnohočleny na součin. (a + b)2 = a 2 + 2 ab + b 2 = (a + b)2 (a – b)2 = a 2 – 2 ab + b 2 2 a – 2 ab + 2 b = (a – 2 b) (a + b). (a – b) = a 2 – b 2 = (a + b). (a – b)

Použité obrázky: Všechny uveřejněné odkazy [cit. 2010– 25– 06]. Dostupné pod licencí Creative Commons na http: //www. clker. com. Obrázek na pozadí: [cit. 2010 -10 -19]. Dostupný pod licencí Public domain na www: <http: //www. clker. com/clipart-blackboard. html> Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Radomír Macháň. Dostupné z Metodického portálu www. rvp. cz, ISSN: 1802 -4785, financovaného z ESF a státního rozpočtu ČR. Provozováno Výzkumným ústavem pedagogickým v Praze.