Rotational Dynamics Torque Angular Acceleration AH Physics Mr

Rotational Dynamics Torque & Angular Acceleration AH Physics Mr Stewart

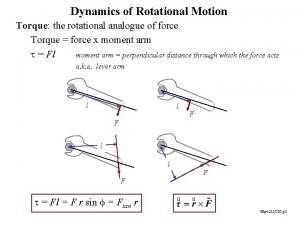
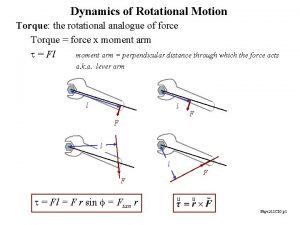
Torque A force that produces a turning effect on an object is called a torque. The turning effect depends on: �Size of the force (F) applied (at a tangent to the circle) �Distance from the axis of rotation to the force (r) T = torque in newton metres (N m) F = force in newtons (N) r = radius in metres (m) Note: The force applied is perpendicular to the radius.

Example a) A driver is removing the wheel nuts from a car wheel when changing the tyre after getting a puncture. She applies a force of 65 N perpendicular to the wheel wrench (spanner) at a distance of 0. 4 m from the centre of the nut. Calculate the applied torque. b) One of the wheel nuts is stuck. Suggest 2 ways in which she could apply a greater torque to remove the nut. T = Fr = 65 x 0. 4 = 26 N m. Greater force at same distance or same force at greater distance (longer spanner)

Unbalanced torque �This is similar to Newtons 2 nd Law F= ma �An unbalanced torque will produce an angular acceleration about an axis of rotation. The rotational equivalent of mass is called the moment of inertia (I) of an object. It depends on the mass of the object itself and the distribution of mass about its axis of rotation. T = torque measured in newton metres (N m) I = moment of inertia measured in kg m 2 α = angular acceleration (rad s-2) Moment of inertia is sometimes referred to as “rotational mass” and is very important in rotational motion.

Moment of Inertia (I) The moment of inertia of an object (I) is a measure of its reluctance to a change in its rotational motion. It depends on the mass of the object and the distribution of its mass about its axis of rotation. The expression for the moment of inertia of a point mass (m) located at a distance (r) from the axis of rotation can be derived by thinking about Newtons 2 nd Law Multiply both sides by r Torque T = Fr angular acceleration α =a/r a=αr Moment of inertia (kg m 2) Radius 2 (m 2) Mass (kg)

Moment of inertia for different objects Different objects have different expressions for their moment of inertia. It depends on the distribution of the mass around the axis of rotation. Typical examples are given on the relationships sheet. (A capital M is often used to denote the total mass of the object. ) Think : Why is the moment of inertia of a disc half that of a hoop of the same mass?

Torque & Moment of inertia example (2017) I = ½ mr 2 I = ½ x 0. 4 x 0. 292 I = 0. 017 kg m 2

(i) T= Fr = 8 x 0. 0075 = 0. 06 N m (ii) T = I α 0. 06 = 0. 017 x α α = 3. 5 rad s-2

Rotational kinetic energy In linear motion, kinetic energy is given by: (All particles in an object moving at a constant linear velocity are moving at the same speed. ) In rotational motion, however, the particles in a disc rotating at a constant rate all have different speeds, a particle at the edge is moving faster than a particle near the axis of rotation, but……… they all have the same angular velocity So we need a new relationship for rotational kinetic energy that uses angular velocity. The quantity (mr 2) is called the moment of inertia (or “rotational mass”) of a point mass undergoing rotational motion. It is given the symbol I.

Rotational Kinetic Energy �Rotational kinetic energy is similar to linear kinetic energy but you must use the moment of inertia (in place of mass) and the angular velocity A washing machine drum can be considered to be a hollow cylinder (a hoop) of mass 8 kg and radius 20 cm. Determine the rotational kinetic energy of the drum when it is spinning at a) 400 rpm b) 1600 rpm. Moment of inertia of a hoop is (mr 2). Angular velocity ω =2π/60 x rpm a) 280 J b) 4500 J

Total kinetic energy If an object has a combination of linear and rotational motion e. g. a car wheel rolling along a road, you can determine the total kinetic energy simply by adding the linear (translational) and rotational kinetic energies. This has some interesting consequences for cylinders rolling down a slope……

Rolling Cylinders - Demo 2 cylinders of the same mass and diameter are released from the same height on a slope. One is solid, the other is hollow. Which one, if any, reaches the bottom first? Walter Lewin demo watch from 4: 50 seconds. Think…. • Does mass matter? • Does diameter matter? • Does length matter?

Experiment – hollow and solid cylinders �Measure the mass of each cylinder. �Measure the radius of each cylinder �Calculate the moment of inertia of each cylinder. By using conservation of energy, determine the moment of inertia of each cylinder experimentally: • Measure the vertical height of the slope. • Calculate the initial potential energy of the cylinders. (Ep = mgh) • Measure the length of the slope. • Measure the time taken for each cylinder to roll down the slope. • Determine the final linear and angular velocity of each cylinder at the bottom of the slope using: Determine experimentally the moment of inertia, I, of each cylinder from these results using: Which method is better? (Q 16. 2016 paper)

Connected systems – The Flywheel (only for the brave) A 2. 50 kg mass is attached to a 25. 0 kg flywheel with a long string that is wound onto the flywheel that has a radius of 0. 30 m and is free to rotate. The hanging mass is held stationary and then allowed to fall through a height of 2. 00 m. As it falls the flywheel accelerates angularly. a) b) c) d) e) Calculate the initial potential energy of the hanging mass. Calculate the moment of inertia of the flywheel. (a disc) Using conservation of energy, determine the final velocity of the mass. Calculate the acceleration of the falling mass a) Ep = mgh = 49 J Calculate the angular acceleration of the flywheel b) I = 1/2 mr 2 = 1. 125 kg m 2

Angular Momentum �Remember at Higher: momentum = mass x velocity �Well, at Advanced Higher we need to be able to understand angular momentum. Angular momentum = moment of inertia x angular velocity Units kg m 2 rad s-1 The same rules apply : “ angular momentum is conserved in the absence of any external torques” Total angular momentum before = total angular momentum after Also: Angular momentum = linear momentum x radius

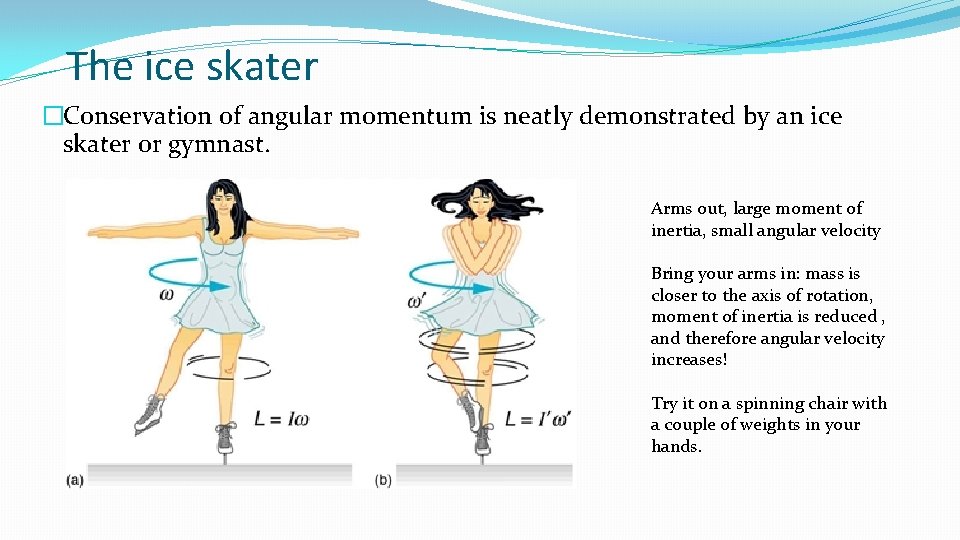
The ice skater �Conservation of angular momentum is neatly demonstrated by an ice skater or gymnast. Arms out, large moment of inertia, small angular velocity Bring your arms in: mass is closer to the axis of rotation, moment of inertia is reduced , and therefore angular velocity increases! Try it on a spinning chair with a couple of weights in your hands.

Example �An ice skater rotates at 3 rad s-1 with her arms outstretched. Her moment of inertia in this position is 3. 8 kg m 2. She now bring her arms in and her moment of inertia decreases to 1. 14 kg m 2 �a) Calculate her angular velocity when she brings her arms in. �b) Show that her rotational kinetic energy increases by 40 J �c) Explain where this extra energy comes from. b) Ekb = 17 J Eka = 57 J Increase = 40 J. c) Work done in pulling her arms in. ω2 = 10 rad s-1

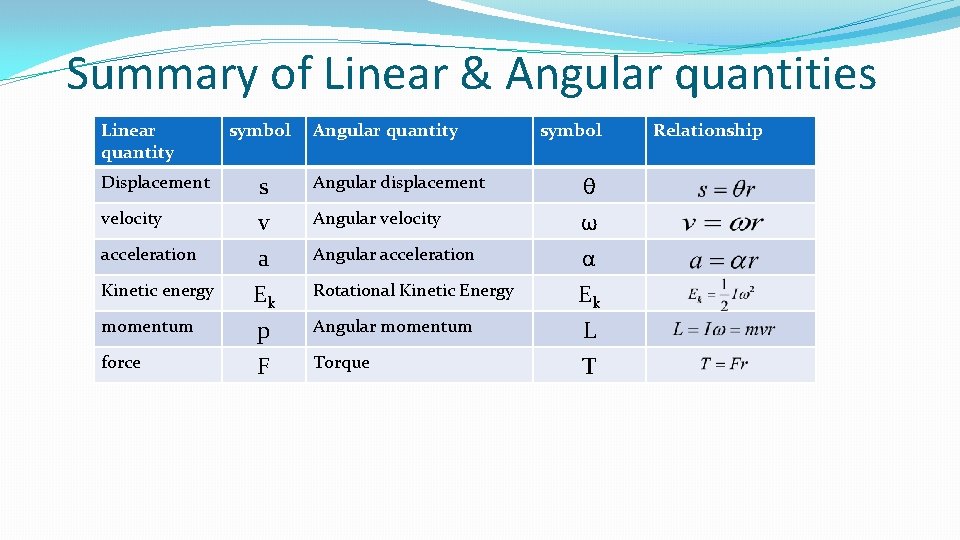
Summary of Linear & Angular quantities Linear quantity symbol Displacement s velocity acceleration Kinetic energy momentum force v a Ek p F Angular quantity Angular displacement Angular velocity Angular acceleration Rotational Kinetic Energy Angular momentum Torque symbol Relationship

Summary of Linear & Angular quantities Linear quantity symbol Displacement s velocity acceleration Kinetic energy momentum force v a Ek p F Angular quantity Angular displacement Angular velocity Angular acceleration Rotational Kinetic Energy Angular momentum Torque symbol Relationship θ ω α Ek L T