ROTATIONAL MOTION Angular Displacement Velocity and Acceleration Rotational

ROTATIONAL MOTION • Angular Displacement, Velocity, and Acceleration • Rotational Energy • Moment of Inertia • Torque • Work, Power and Energy in Rotational Motion

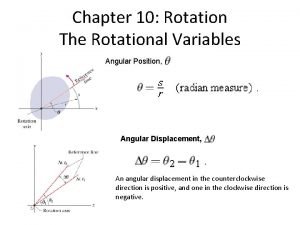
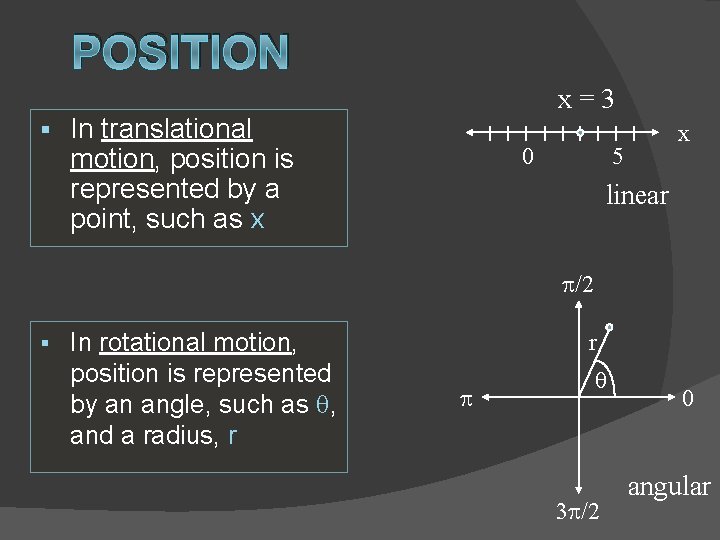
POSITION § x=3 In translational motion, position is represented by a point, such as x 0 x 5 linear p/2 § In rotational motion, position is represented by an angle, such as q, and a radius, r r p q 3 p/2 0 angular

DISPLACEME NT § Linear displacement is Dx = - 4 represented by the vector Dx Angular displacement is represented by Dq, which is not a vector, but behaves like one for small values. § The right hand rule determines direction 0 x 5 linear p/2 § Dq p 0 3 p/2 angular

TANGENTIAL AND ANGULAR DISPLACEMENT s § § A particle that rotates through an angle Dq also translates through a distance s, which is the arc length of its path This distance s is related to the angular displacement Dq by the equation s = r. Dq Dq r

§ SPEED AND VELOCITY The instantaneous velocity has magnitude v. T = ds/dt and is tangent to the circle s v. T Dq v. T r is outward according to RHR The same particle rotates with an angular velocity = dq/dt § The direction of the angular velocity is given by the right hand rule § Tangential and angular speeds are related by the equation v = r §

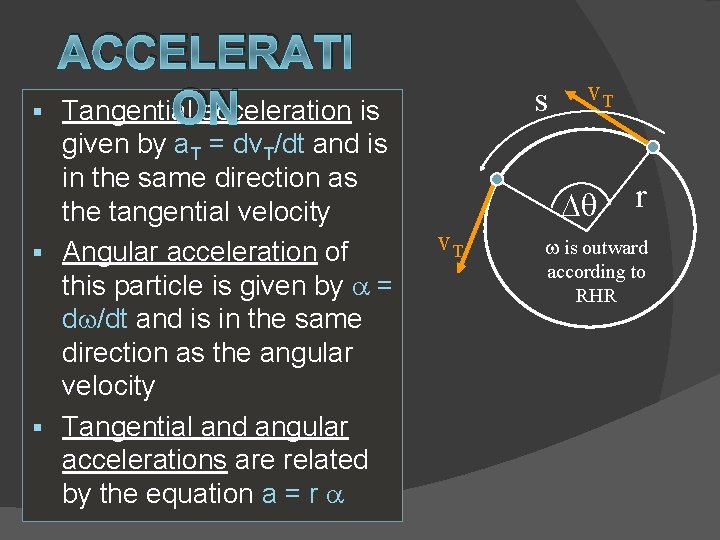
§ ACCELERATI Tangential acceleration is ON given by a. T = dv. T/dt and is in the same direction as the tangential velocity § Angular acceleration of this particle is given by = d /dt and is in the same direction as the angular velocity § Tangential and angular accelerations are related by the equation a = r s v. T Dq v. T r is outward according to RHR

First Kinematic Equation § v = vo + at (linear form) § Substitute angular velocity for velocity § Substitute angular acceleration for acceleration § = o + t (angular form)

Second Kinematic Equation § x = xo + vot + ½ at 2 (linear form) § Substitute angle for position § Substitute angular velocity for velocity § Substitute angular acceleration for acceleration § q = qo + ot + ½ t 2 (angular form)

Third Kinematic Equation § v 2 = vo 2 + 2 a(x - xo) (linear form) § Substitute angle for position § Substitute angular velocity for velocity § Substitute angular acceleration for acceleration § 2 = o 2 + 2 (q - qo) (angular form)

Summary of Angular Kinematics

Practice Problem: A turntable rotates with a constant angular acceleration of 5. 60 rad/s 2 and the angular speed of the turntable is 3. 00 rad/s at t = 0. Through what angle does the wheel rotate in 4. 00 seconds? b) What is the angular speed at t = 4. 00 s? a) a) 56. 8 rad or 3254° b) 25. 6 rad/s

Practice problem: The angular velocity of a flywheel is described by the equation = (8. 00 – 2. 00 t 2). Determine the angular displacement when the flywheel reverses its direction. (changes direction @ t = 2 s) 10. 67 rad or 611°

ROTATIONAL ENERGY § Bodies moving in a straight line have translational kinetic energy § KE= ½mv 2 § Although every particle has the same angular speed ω, the individual linear speeds depend on their distance from the axis of rotation (v = rω) § The TOTAL Kinetic Energy of a rotating object comes from adding the Kinetic Energies of each individual particle: § KER= ΣKE = Σ ½mv 2 = ½Σmr 2ω2

ROTATIONAL ENERGY AND MOMENT OF INERTIA 2 2 § KE = ½Σmr ω = ½ (Σmr 2) ω2 R § The ½ and ω are common to every term § The quantity (Σmr 2) is called the Moment of Inertia § I = Σmr 2 § The moment of Inertia has dimensions of ML 2 (kg m 2) § We can then describe the Rotational Kinetic Energy of an object as: § KER = ½Iω2 § This is not a new type of energy, and it is possible to have both forms at once § Ktot = ½ m v 2 + ½ I 2

MOMENT OF INERTIA § Moment of inertia, also referred to as the rotational inertia or the angular mass, is a measure of an object’s resistance to a change in it’s rotation rate § The role of moment of inertia in rotational dynamics is analogous to mass in linear dynamics (which is a measure of an object’s resistance to a change in motion)

MOMENT OF INERTIA § I = mr 2 (for a system of particles) § I = lim mr 2 § I = dm r 2 (for a solid object) § dm = λd. L § dm = σd. A § dm = ρd. V

Practice Problem: A 3. 0 m long lightweight rod has a 1. 0 kg mass attached to one end, and a 1. 5 kg mass attached to the other. If the rod is spinning at 20 rpm about its midpoint around an axis that is perpendicular to the rod, what is the resulting rotational kinetic energy? Ignore the mass of the rod. KErot=12. 3 J

Practice Problem: Calculate the Moment of Inertia of a uniform hoop of mass M and radius R.

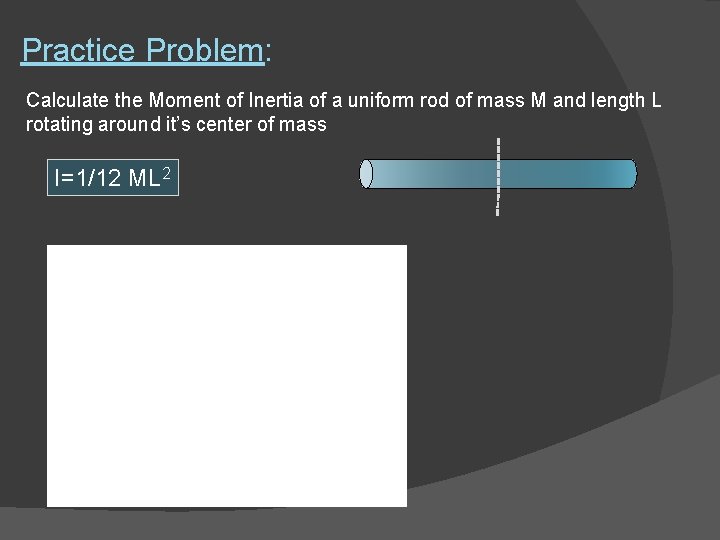
Practice Problem: Calculate the Moment of Inertia of a uniform rod of mass M and length L rotating around it’s center of mass I=1/12 ML 2

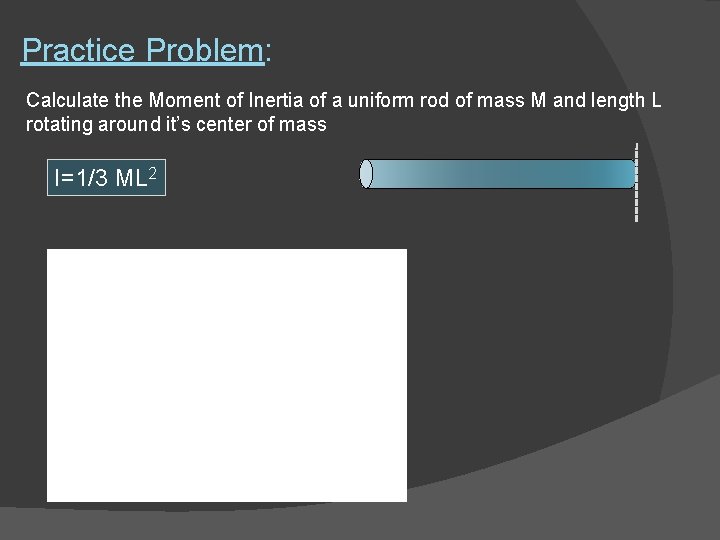
Practice Problem: Calculate the Moment of Inertia of a uniform rod of mass M and length L rotating around it’s center of mass I=1/3 ML 2

PARALLEL AXIS THEOREM � If you know the moment of Inertia about the center of mass of an object, you can find the moment of inertia about any other axis parallel to the original one. I = Icm + MD 2

Parallel axis theorem: Example � Find the moment of inertia of a uniform rigid rod of mass M and length L about an axis perpendicular to the rod through one end � Icm = The moment of inertia around the center of mass of an object � D = the distance from the COM of an object to the new axis of rotation I = Icm + MD 2

Parallel axis theorem: Example � Find the moment of inertia of a uniform rigid rod of mass M and length L about an axis perpendicular to the rod through one end I = Icm + MD 2 I = 1/12 ML 2 M(L/2)2 = 1/3 ML 2 � Recall That:

EQUILIBRIUM � Equilibrium occurs when there is no net force and no net torque on a system � Static equilibrium occurs when nothing in the system is moving or rotating in your reference frame � Dynamic equilibrium occurs when the system is translating at constant velocity and/or rotating at constant rotational velocity � Conditions for equilibrium: � = 0 � F = 0

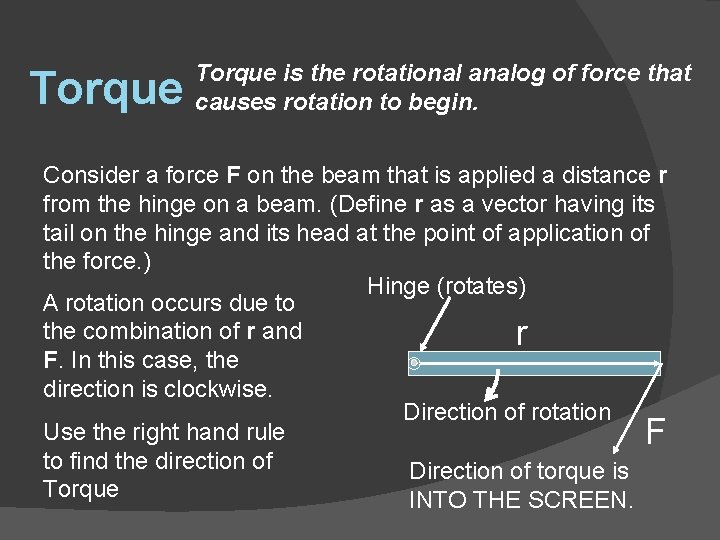
Torque is the rotational analog of force that causes rotation to begin. Consider a force F on the beam that is applied a distance r from the hinge on a beam. (Define r as a vector having its tail on the hinge and its head at the point of application of the force. ) Hinge (rotates) A rotation occurs due to the combination of r and r F. In this case, the direction is clockwise. Direction of rotation Use the right hand rule F to find the direction of Direction of torque is Torque INTO THE SCREEN.

Calculating Torque The magnitude of the torque is proportional to that of the force and moment arm, and torque is at right angles to the plane established by the force and moment arm vectors. (aka a Cross Product) � = r F = Frsinθ � � : torque � r: moment arm (from point of rotation to point of application of force) � F: force

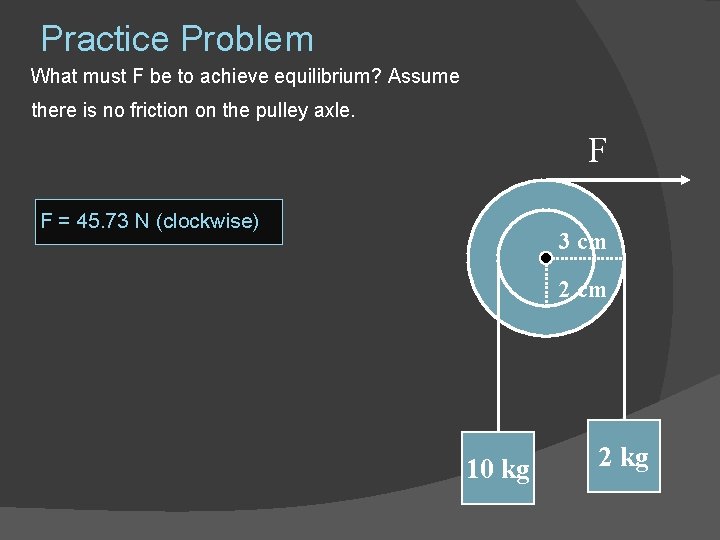
Practice Problem What must F be to achieve equilibrium? Assume there is no friction on the pulley axle. F F = 45. 73 N (clockwise) 3 cm 2 cm 10 kg 2 kg

Torque and Newton’s Law nd 2 � Rewrite F = ma for rotating systems �Substitute torque force �Substitute rotational inertia for mass �Substitute angular acceleration for acceleration � = I � : torque �I: rotational inertia � : angular acceleration

Torque and Newton’s Law nd 2 � Rewrite F = ma for rotating systems � = Fr = (ma)r �Remember that a = αr � = Fr = (ma)r = m(αr)r = (mr 2) α � =I

Practice Problem A 1. 0 -kg wheel of 25 -cm radius is at rest on a fixed axis. A force of 0. 45 N is applied tangent to the rim of the wheel for 5 seconds. What is the angular acceleration of the wheel? b) After this time, what is the angular velocity of the wheel? c) Through what angle does the wheel rotate during this 5 second period? a) a) 1. 8 rad/s 2 b) 9 rad/s c) 45 rad or 2578°

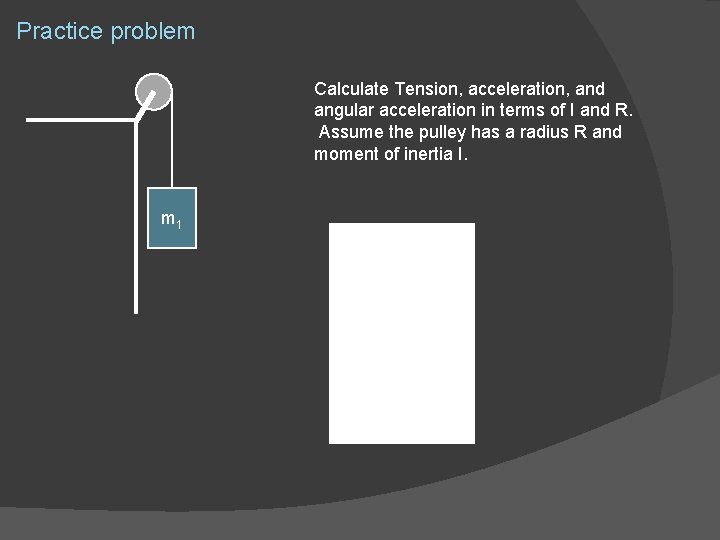
Practice problem Calculate Tension, acceleration, and angular acceleration in terms of I and R. Assume the pulley has a radius R and moment of inertia I. m 1

WORK AND POWER IN ROTATING SYSTEMS

Work in rotating systems � W = F • Dr (translational systems) �Substitute torque force �Substitute angular displacement for displacement � Wrot = • Dq �Wrot : work done in rotation � : torque �Dq: angular displacement � Remember that different kinds of work change different kinds of energy: �Wnet = DK Wc = -DU Wnc = DE

Power in rotating systems P = d. W/dt (in translating or rotating systems) � P = F • v (translating systems) � �Substitute torque force �Substitute angular velocity for velocity � Prot = • (rotating systems) �Prot : power expended � : torque � : angular velocity

Conservation of Energy � Etot = U + K = Constant �(rotating or linear system) �For gravitational systems, use the center of mass of the object for calculating U �Use rotational and/or translational kinetic energy where necessary

Practice problem A rod with mass M and length L is free to rotate around the pivot point at one end of the rod. The rod is held at the horizontal position and let go starting from rest. a) Calculate the angular velocity of the rod when the rod is at it’s lowest position b) Calculate the linear velocity of the center of mass of the rod at it’s lowest position c) Calculate the linear velocity of the end of the rod at it’s lowest position a) ω=(3 g/L)1/2 b) V = ½ (3 gl)1/2 c) V = (3 gl)1/2

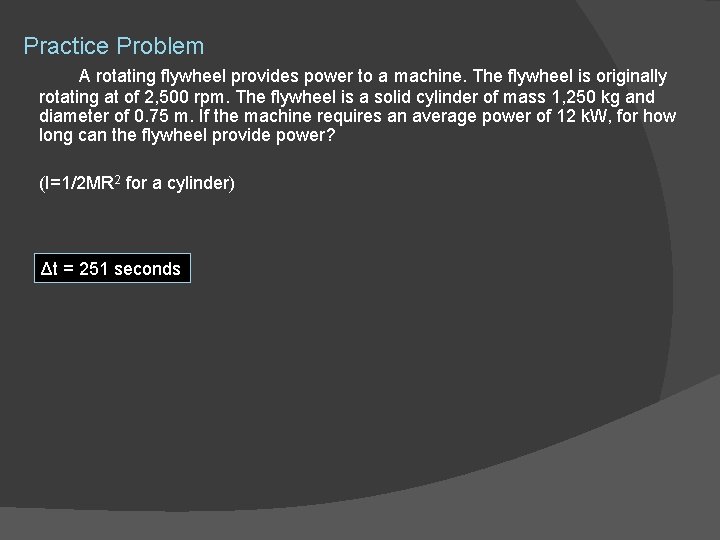
Practice Problem A rotating flywheel provides power to a machine. The flywheel is originally rotating at of 2, 500 rpm. The flywheel is a solid cylinder of mass 1, 250 kg and diameter of 0. 75 m. If the machine requires an average power of 12 k. W, for how long can the flywheel provide power? (I=1/2 MR 2 for a cylinder) Δt = 251 seconds