Chapter 11 Angular Momentum Rolling Torque and Angular

Chapter 11 Angular Momentum

Rolling, Torque, and Angular Momentum I. Rolling II. IV. II. Torque - Kinetic energy - Forces III. Angular momentum - Definition IV. Newton’s second law in angular form V. Angular momentum - System of particles - Rigid body - Conservation

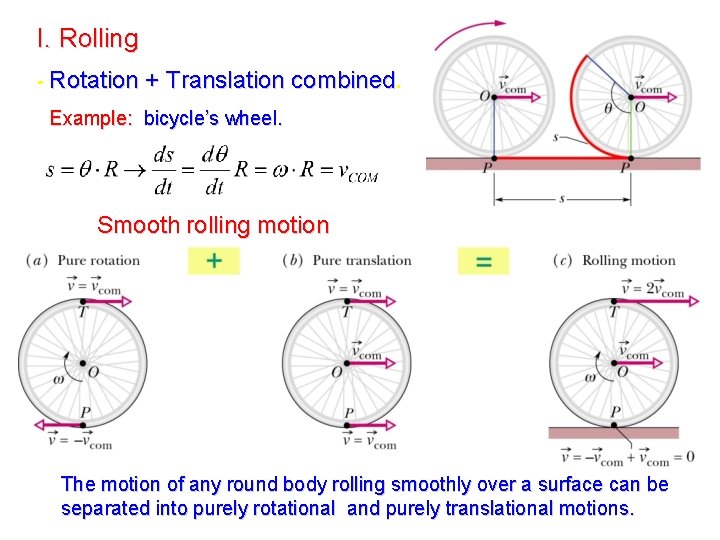
I. Rolling - Rotation + Translation combined. Example: bicycle’s wheel. Smooth rolling motion The motion of any round body rolling smoothly over a surface can be separated into purely rotational and purely translational motions.

- Pure rotation. Rotation axis through point where wheel contacts ground. Angular speed about P = Angular speed about O for stationary observer. Instantaneous velocity vectors = sum of translational and rotational motions. - Kinetic energy of rolling. A rolling object has two types of kinetic energy (about its COM). Rotational: (translation of its COM). Translational:

- Forces of rolling. (a)Rolling at constant speed no sliding at P no friction. (b) Rolling with acceleration sliding at P friction force opposed to sliding. Static friction wheel does not slide smooth rolling motion a. COM = α R Sliding Increasing acceleration Example 1: wheels of a car moving forward while its tires are spinning madly, leaving behind black stripes on the road rolling with slipping = skidding Icy pavements. Antiblock braking systems are designed to ensure that tires roll without slipping during braking.

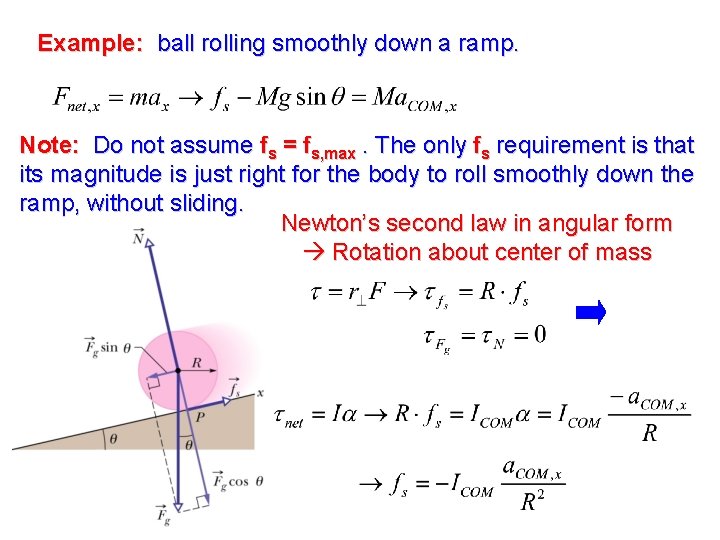
Example 2: ball rolling smoothly down a ramp. (No slipping). 1. Frictional force causes the rotation. Without friction the ball will not roll down the ramp, will just slide. Sliding tendency 2. Rolling without sliding the point of contact between the sphere and the surface is at rest the frictional force is the static frictional force. 3. Work done by frictional force = 0 the point of contact is at rest (static friction).

Example: ball rolling smoothly down a ramp. Note: Do not assume fs = fs, max. The only fs requirement is that its magnitude is just right for the body to roll smoothly down the ramp, without sliding. Newton’s second law in angular form Rotation about center of mass

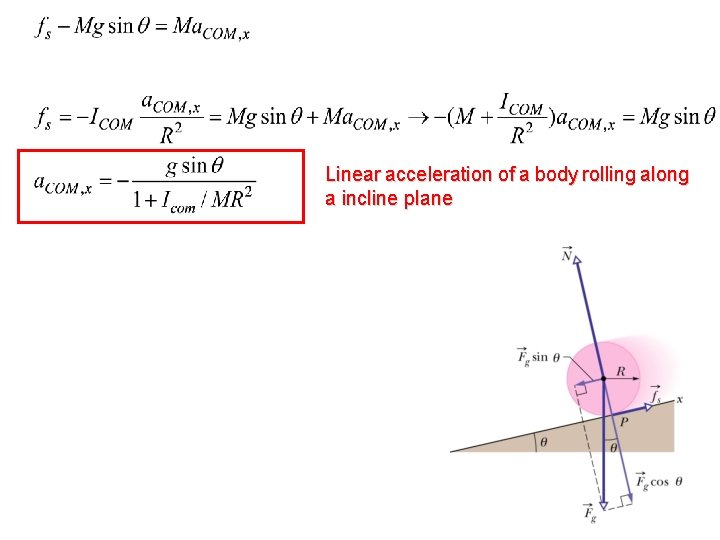
Linear acceleration of a body rolling along a incline plane

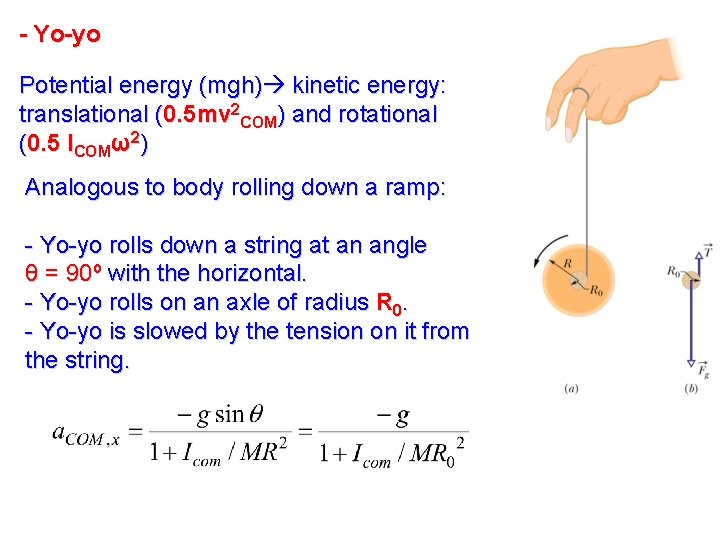
- Yo-yo Potential energy (mgh) kinetic energy: translational (0. 5 mv 2 COM) and rotational (0. 5 ICOMω2) Analogous to body rolling down a ramp: - Yo-yo rolls down a string at an angle θ = 90º with the horizontal. - Yo-yo rolls on an axle of radius R 0. - Yo-yo is slowed by the tension on it from the string.

II. Torque - Vector quantity. Direction: right hand rule. Magnitude: Torque is calculated with respect to (about) a point. Changing the point can change the torque’s magnitude and direction.

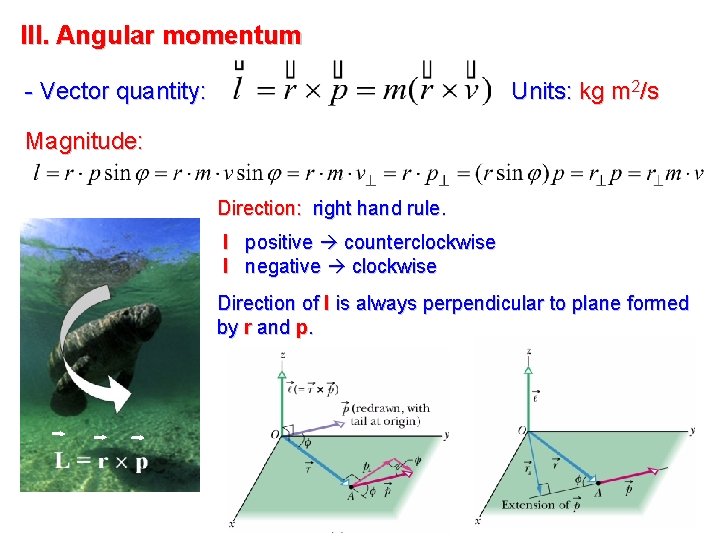
III. Angular momentum - Vector quantity: Units: kg m 2/s Magnitude: Direction: right hand rule. l positive counterclockwise l negative clockwise Direction of l is always perpendicular to plane formed by r and p.

IV. Newton’s second law in angular form Linear Angular Single particle The vector sum of all torques acting on a particle is equal to the time rate of change of the angular momentum of that particle. Proof: V. Angular momentum - System of particles:

Includes internal torques (due to forces between particles within system) and external torques (due to forces on the particles from bodies outside system). Forces inside system third law force pairs torqueint sum =0 The only torques that can change the angular momentum of a system are the external torques acting on a system. The net external torque acting on a system of particles is equal to the time rate of change of the system’s total angular momentum L.

- Rigid body (rotating about a fixed axis with constant angular speed ω): Magnitude Direction: li perpendicular to ri and pi Rotational inertia of a rigid body about a fixed axis

- Conservation of angular momentum: Newton’s second law If no net external torque acts on the system (isolated system) Law of conservation of angular momentum: Net angular momentum at time ti = Net angular momentum at later time tf If the net external torque acting on a system is zero, the angular momentum of the system remains constant, no matter what changes take place within the system.

If the component of the net external torque on a system along a certain axis is zero, the component of the angular momentum of the system along that axis cannot change, no matter what changes take place within the system. This conservation law holds not only within the frame of Newton’s mechanics but also for relativistic particles (speeds close to light) and subatomic particles. ( Ii, f, ωi, f refer to rotational inertia and angular speed before and after the redistribution of mass about the rotational axis ).

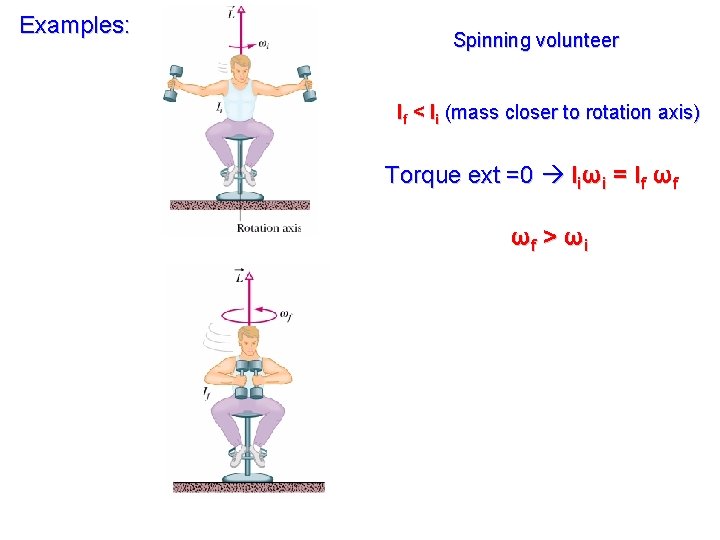
Examples: Spinning volunteer If < Ii (mass closer to rotation axis) Torque ext =0 Iiωi = If ωf ωf > ωi

Springboard diver - Center of mass follows parabolic path. - When in air, no net external torque about COM Diver’s angular momentum L constant throughout dive (magnitude and direction). - L is perpendicular to the plane of the figure (inward). - Beginning of dive She pulls arms/legs closer Intention: I is reduced ω increases - End of dive layout position Purpose: I increases slow rotation rate less “water-splash”

Rotation Translation Torque Force Linear momentum (system of particles, rigid body) Newton’s second law Conservation law (Closed isolated system) Angular momentum System of particles Rigid body, fixed axis L=component along that axis. Newton’s second law Conservation law (Closed isolated system) system

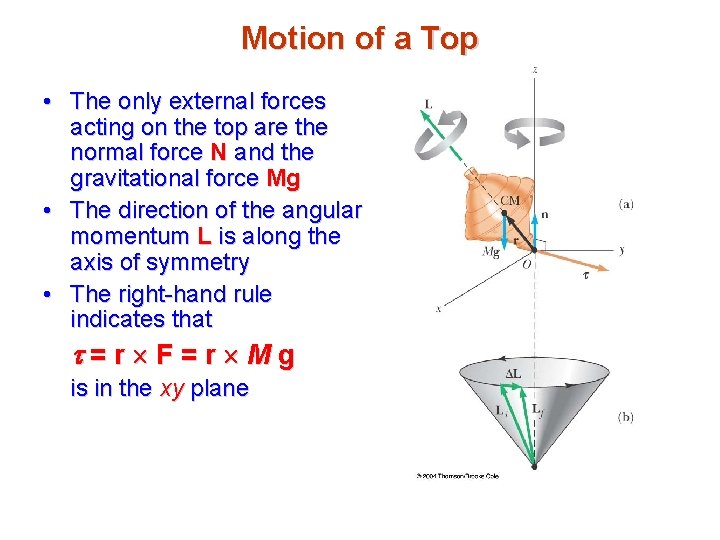
Motion of a Top • The only external forces acting on the top are the normal force N and the gravitational force Mg • The direction of the angular momentum L is along the axis of symmetry • The right-hand rule indicates that =r F=r Mg is in the xy plane

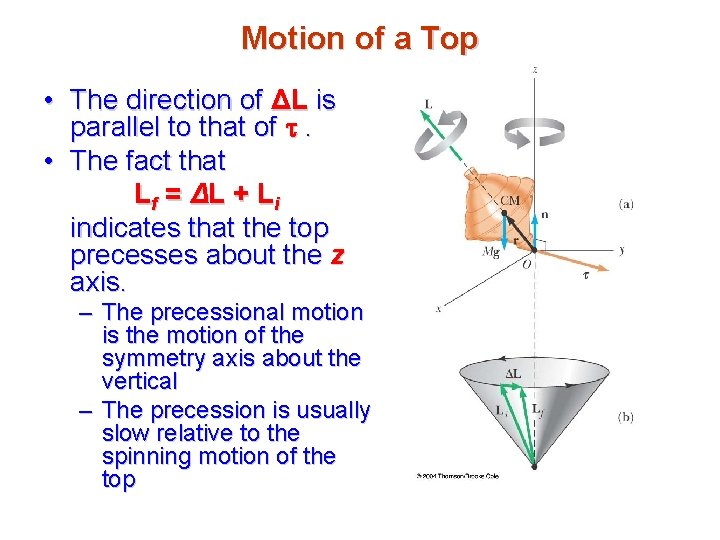
Motion of a Top • The direction of ΔL is parallel to that of . • The fact that L f = ΔL + L i indicates that the top precesses about the z axis. – The precessional motion is the motion of the symmetry axis about the vertical – The precession is usually slow relative to the spinning motion of the top

Gyroscope • A gyroscope can be used to illustrate precessional motion • The gravitational force Mg produces a torque about the pivot, and this torque is perpendicular to the axle • The normal force produces no torque

Gyroscope • The torque results in a change in angular momentum d. L in a direction perpendicular to the axle. The axle sweeps out an angle df in a time interval dt. • The direction, not the magnitude, of L is changing • The gyroscope experiences precessional motion

Gyroscope • To simplify, assume the angular momentum due to the motion of the center of mass about the pivot is zero – Therefore, the total angular momentum is L = Iw due to its spin – This is a good approximation when w is large

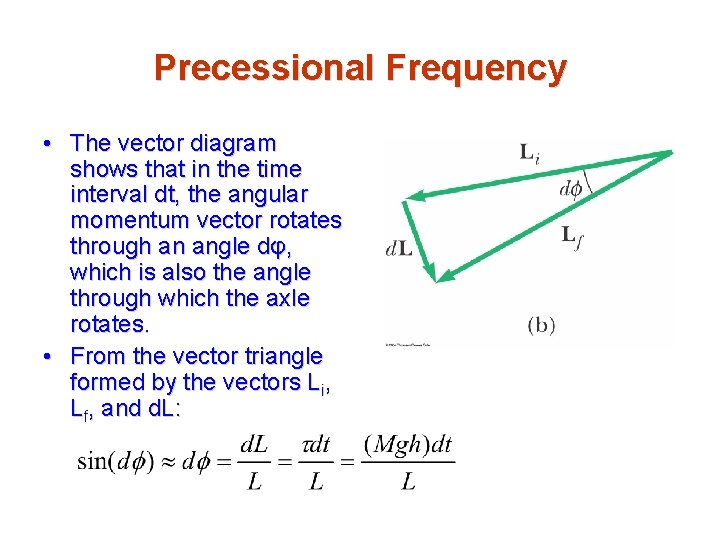
Precessional Frequency • The vector diagram shows that in the time interval dt, the angular momentum vector rotates through an angle dφ, which is also the angle through which the axle rotates. • From the vector triangle formed by the vectors Li, Lf, and d. L:

Precessional Frequency • Analyzing the previous vector triangle, the rate at which the axle rotates about the vertical axis can be found wp is the precessional frequency

Gyroscope in a Spacecraft • The angular momentum of the spacecraft about its center of mass is zero • A gyroscope is set into rotation, giving it a nonzero angular momentum • The spacecraft rotates in the direction opposite to that of the gyroscope • So the total momentum of the system remains zero

V. Precession of a gyroscope wheel fixed to shaft and free to spin about shaft’s axis. Gyroscope: Non-spinning gyroscope If one end of shaft is placed on a support and released Gyroscope falls by rotating downward about the tip of the support. The torque causing the downward rotation (fall) changes angular momentum of gyroscope. Torque caused by gravitational force acting on COM.

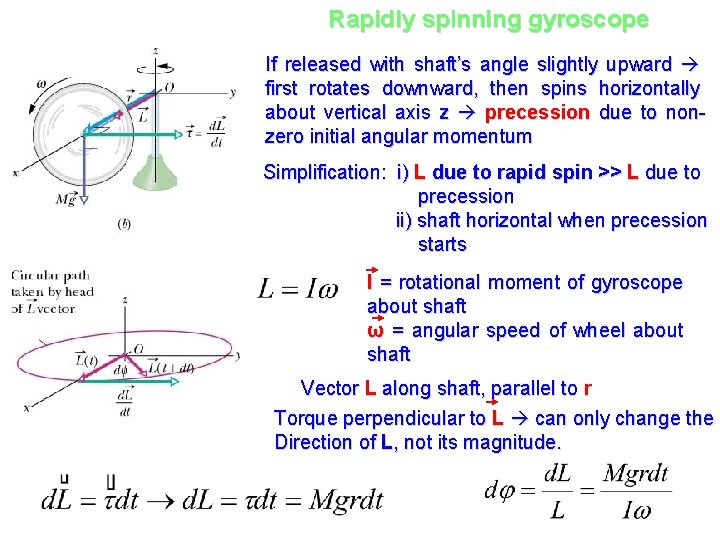
Rapidly spinning gyroscope If released with shaft’s angle slightly upward first rotates downward, then spins horizontally about vertical axis z precession due to nonzero initial angular momentum Simplification: i) L due to rapid spin >> L due to precession ii) shaft horizontal when precession starts I = rotational moment of gyroscope about shaft ω = angular speed of wheel about shaft Vector L along shaft, parallel to r Torque perpendicular to L can only change the Direction of L, not its magnitude.

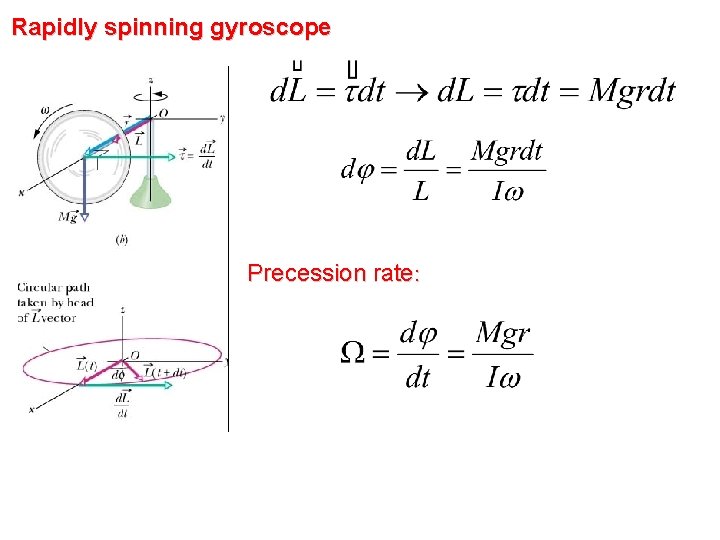
Rapidly spinning gyroscope Precession rate:

A solid cylinder of radius 15 cm and mass 3. 0 kg rolls without slipping at a constant speed of 1. 6 m/s. (a) What is its angular momentum about its symmetry axis? (b) What is its rotational kinetic energy? (c) What is its total kinetic energy? ( I cylinder= )

A solid cylinder of radius 15 cm and mass 3. 0 kg rolls without slipping at a constant speed of 1. 6 m/s. (a) What is its angular momentum about its symmetry axis? (b) What is its rotational kinetic energy? (c) What is its total kinetic energy? ( I cylinder= ) (a) The angular speed of the cylinder is rotational inertia for cylinder , the . The angular momentum about the symmetry axis is

A solid cylinder of radius 15 cm and mass 3. 0 kg rolls without slipping at a constant speed of 1. 6 m/s. (a) What is its angular momentum about its symmetry axis? (b) What is its rotational kinetic energy? (c) What is its total kinetic energy? ( I cylinder= ) (b) (c)

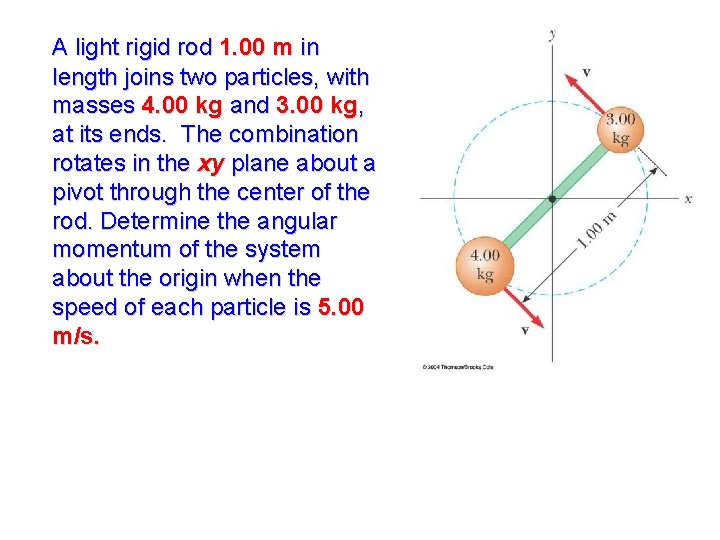
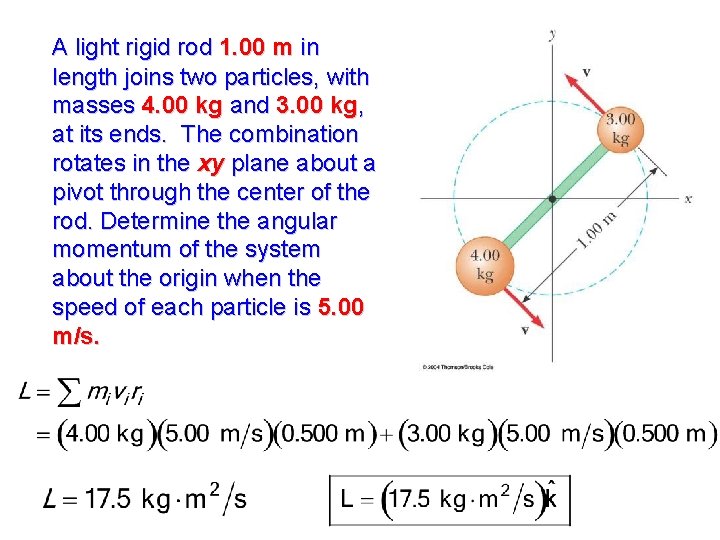
A light rigid rod 1. 00 m in length joins two particles, with masses 4. 00 kg and 3. 00 kg, at its ends. The combination rotates in the xy plane about a pivot through the center of the rod. Determine the angular momentum of the system about the origin when the speed of each particle is 5. 00 m/s.

A light rigid rod 1. 00 m in length joins two particles, with masses 4. 00 kg and 3. 00 kg, at its ends. The combination rotates in the xy plane about a pivot through the center of the rod. Determine the angular momentum of the system about the origin when the speed of each particle is 5. 00 m/s.

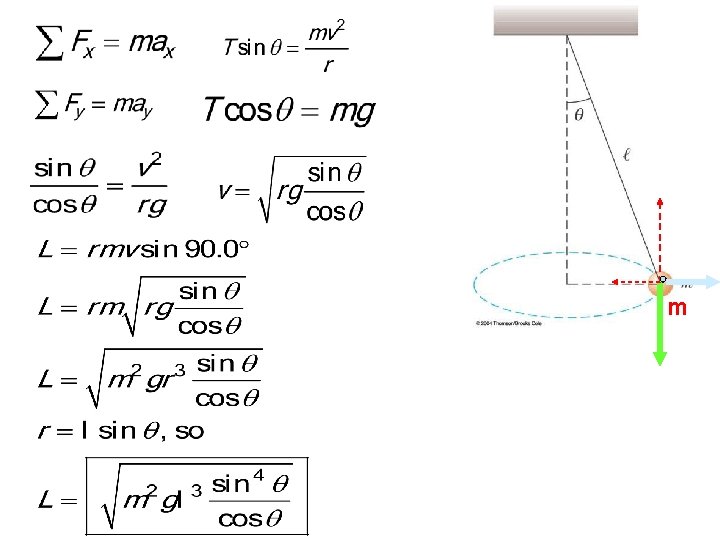
A conical pendulum consists of a bob of mass m in motion in a circular path in a horizontal plane as shown. During the motion, the supporting wire of length maintains the constant angle with the vertical. Show that the magnitude of the angular momentum of the bob about the center of the circle is

m

The position vector of a particle of mass 2. 00 kg is given as a function of time by. Determine the angular momentum of the particle about the origin, as a function of time.

The position vector of a particle of mass 2. 00 kg is given as a function of time by. Determine the angular momentum of the particle about the origin, as a function of time.

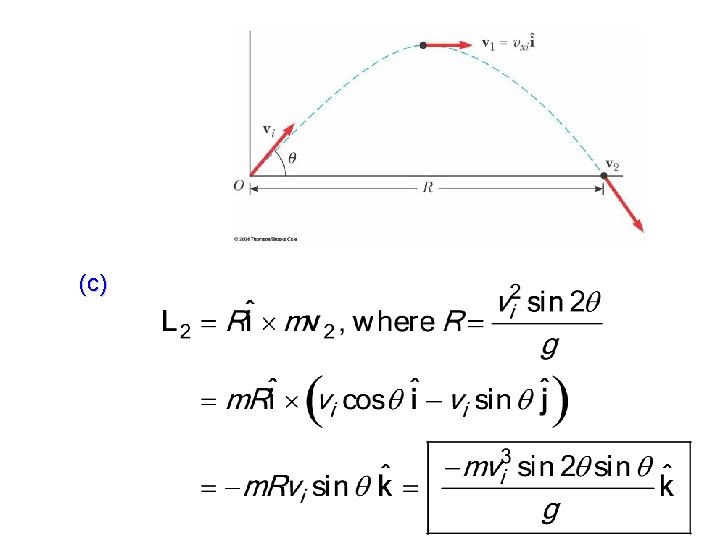
A particle of mass m is shot with an initial velocity vi making an angle with the horizontal as shown. The particle moves in the gravitational field of the Earth. Find the angular momentum of the particle about the origin when the particle is (a) at the origin, (b) at the highest point of its trajectory, and (c) just before it hits the ground. (d) What torque causes its angular momentum to change?

(a) (b) At the highest point of the trajectory,

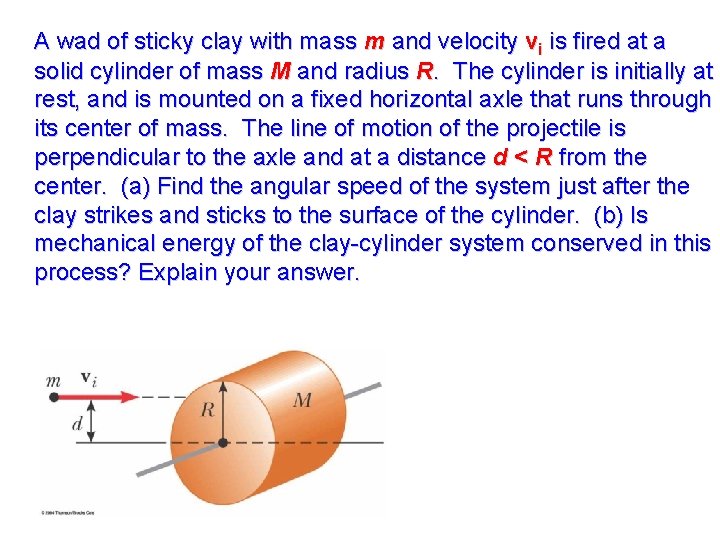
A wad of sticky clay with mass m and velocity vi is fired at a solid cylinder of mass M and radius R. The cylinder is initially at rest, and is mounted on a fixed horizontal axle that runs through its center of mass. The line of motion of the projectile is perpendicular to the axle and at a distance d < R from the center. (a) Find the angular speed of the system just after the clay strikes and sticks to the surface of the cylinder. (b) Is mechanical energy of the clay-cylinder system conserved in this process? Explain your answer.

(a) Consider the system to consist of the wad of clay and the cylinder. No external forces acting on this system have a torque about the center of the cylinder. Thus, angular momentum of the system is conserved about the axis of the cylinder. (b). Some mechanical energy changes to internal energy in this perfectly inelastic collision

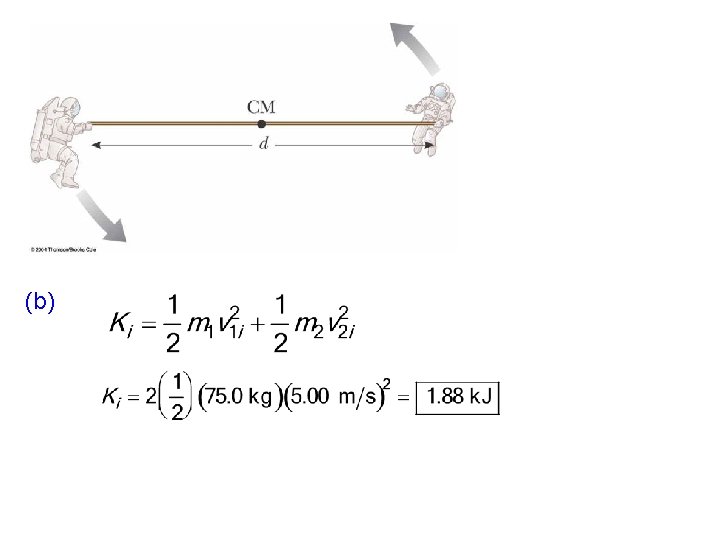
Two astronauts, each having a mass of 75. 0 kg, are connected by a 10. 0 -m rope of negligible mass. They are isolated in space, orbiting their center of mass at speeds of 5. 00 m/s. Treating the astronauts as particles, calculate (a) the magnitude of the angular momentum of the system and (b) the rotational energy of the system. By pulling on the rope, one of the astronauts shortens the distance between them to 5. 00 m. (c) What is the new angular momentum of the system? (d) What are the astronauts’ new speeds? (e) What is the new rotational energy of the system? (f) How much work does the astronaut do in shortening the rope?

(c) Angular momentum is conserved: (d) (e) (f)

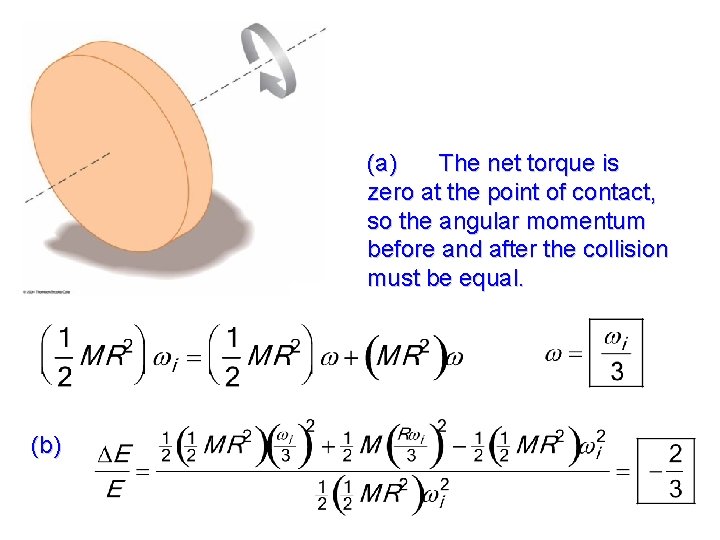
A uniform solid disk is set into rotation with an angular speed ωi about an axis through its center. While still rotating at this speed, the disk is placed into contact with a horizontal surface and released as in Figure. (a) What is the angular speed of the disk once pure rolling takes place? (b) Find the fractional loss in kinetic energy from the time the disk is released until pure rolling occurs. (Hint: Consider torques about the center of mass. )

(a) The net torque is zero at the point of contact, so the angular momentum before and after the collision must be equal. (b)