Rotational Motion Torque Angular Displacement l Angular displacement

Rotational Motion & Torque

Angular Displacement l Angular displacement is a measure of the angle a line from the center to a point on the outside edge sweeps through as the object rotates l We use the greek letter “theta” to represent angular displacement l Angular displacement is measured in “radians”

Arc Length l Arc length is represented by the letter s l it is the distance a point on the edge of the object rotates through l measured in meters r s r

Angular Velocity l Angular velocity is a measure of the rate of change of the angular position or the “spin rate” l We use the greek letter lowercase “omega” ( ) to represent angular velocity mathematically l Angular velocity is measured in “radians per second” (rad/sec)

Angular Velocity r May also be expressed in rpm (revolutions per minute) but must be converted to rad/sec for calculations r

Angular Acceleration l Angular acceleration is the rate of change of angular velocity l We use the greek letter “alpha” to represent angular acceleration l Angular acceleration is measured in radians per second (rad/sec 2)

Angular Acceleration r r

Rotational Motion Relationships

Conversions and signs For rotating objects, clockwise (cw) is negative and counter-clockwise (ccw) is positive. This applies to Ɵ, ɷ, and α. • Conversions: •

What is Torque? l Torque is a measure of how much a force acting on an object causes that object to rotate. l Torque is dependent on force and lever arm and is measured in Newton-meters (Nm)

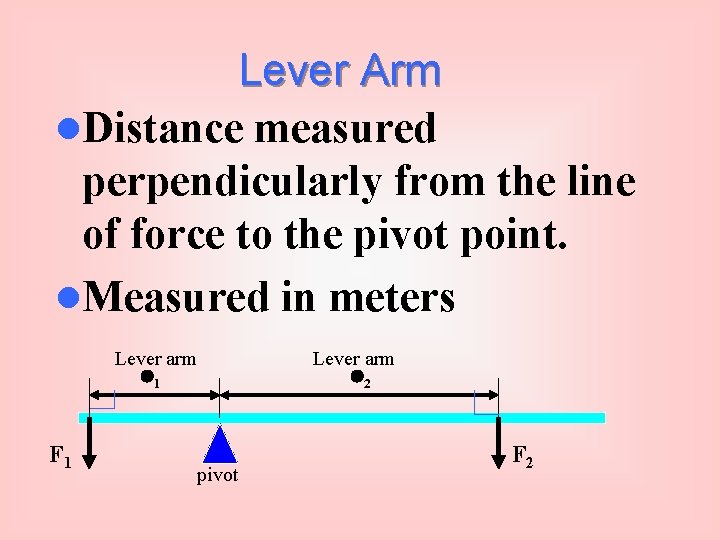
Lever Arm l. Distance measured perpendicularly from the line of force to the pivot point. l. Measured in meters Lever arm 1 F 1 pivot Lever arm 2 F 2

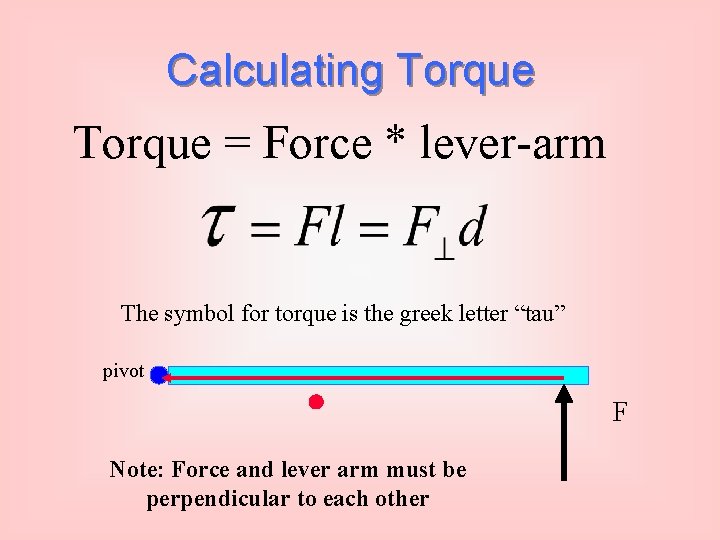
Calculating Torque = Force * lever-arm The symbol for torque is the greek letter “tau” pivot Note: Force and lever arm must be perpendicular to each other F

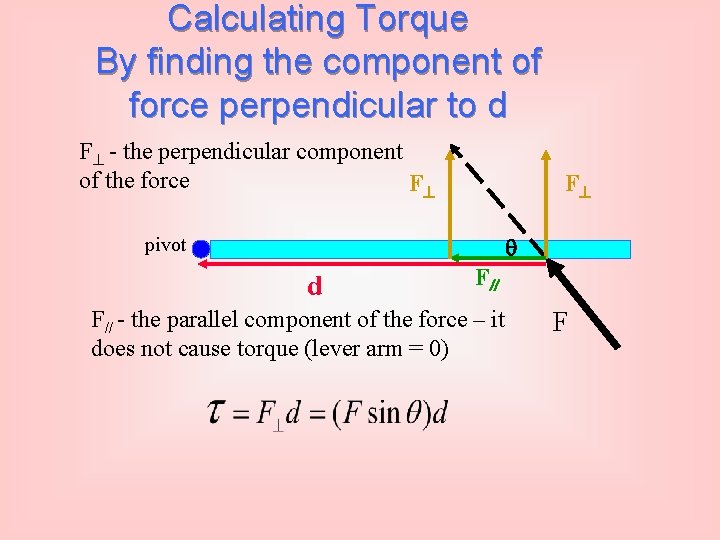
Calculating Torque By finding the component of force perpendicular to d F - the perpendicular component of the force F F pivot d F F// - the parallel component of the force – it does not cause torque (lever arm = 0) F

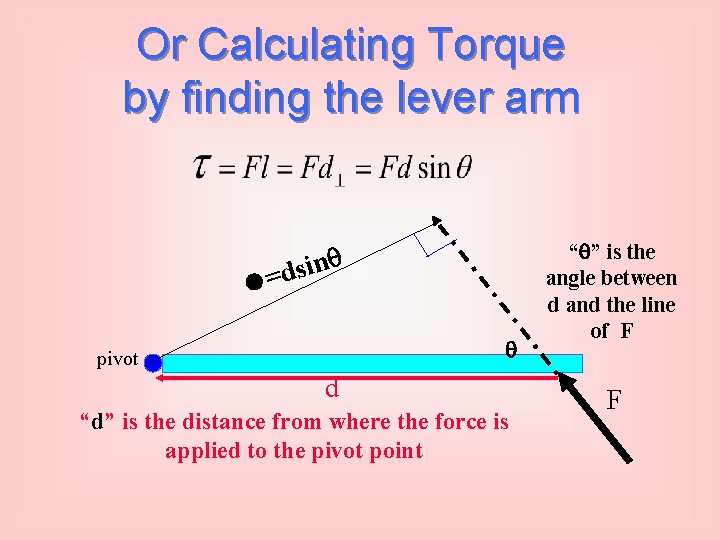
Or Calculating Torque by finding the lever arm n i s d = pivot d “d” is the distance from where the force is applied to the pivot point “ ” is the angle between d and the line of F F

Net Torque l The net torque is the sum of all the individual torques. l Torque that is clockwise (cw) is negative and torque that is counter-clockwise (ccw) is positive.

Rotational Equilibrium In rotational equilibrium, the sum of all the torques is equal to zero. In other words, there is no net torque on the object. • There is no angular acceleration. • The object is either not rotating or it is rotating at a constant speed. • or •

Linear Equilibrium In linear equilibrium, the sum of all the forces is equal to zero. In other words, there is no net force on the object. • There is no linear acceleration. (a = 0) • The object is either not moving linearly or it is moving at a constant velocity. • and •

Total Equilibrium In total equilibrium, both net force and net torque are equal to zero. In other words, there is no net force or net torque on the object. • and • a=0 and α=0 •

l

Moment of Inertia l Also called rotational inertia or angular mass l A quantity expressing a body’s tendancy to resist angular acceleration with the application of a torque l Depends on a body’s mass distribution and the chosen axis of rotation l Determines the torque needed for a desired angular acceleration about a rotational axis

Moment of Inertia l For a point mass: I = mr 2 r m l For a thin hoop about axis of symmetry (through center) I = mr 2 • For a solid disc about axis of symmetry: (through center) I = ½ mr 2 r r

l Angular acceleration is directly related to torque l Angular acceleration is inversely related to moment of inertia

EXAMPLE PROBLEM 1 TORQUE: The Swinging Door Question In a hurry to catch a cab, you rush through a frictionless swinging door and onto the sidewalk. The force you exerted on the door was 50 N, applied perpendicular to the plane of the door. The door is 1. 0 m wide. Assuming that you pushed the door at its edge, what was the torque on the swinging door (taking the hinge as the pivot point)? Hints 1. Where is the pivot point? 2. What was the force applied? 3. How far from the pivot point was the force applied? 4. What was the angle between the door and the direction of force?

Solution The pivot point is at the hinges of the door, opposite to where you were pushing the door. The force you used was 50 N, at a distance 1. 0 m from the pivot point. You hit the door perpendicular to its plane, so the angle between the door and the direction of force was 90 degrees. Since then the torque on the door was: Note: You did not have to τ = (1. 0 m) (50 N) sin(90°) include sinƟ since l is τ = 50 N m given (F l)

EXAMPLE PROBLEM 2 TORQUE: The Swinging Door Question: same problem as problem 1 except now the force is applied at an angle of 80° to the plane of the door. Solution: τ = (1. 0 m) (50 N) sin(80°) τ = 49. 2 N m