REPREZENTAREA SISTEMELOR CU AJUTORUL ECUAIILOR DE STARE Un

REPREZENTAREA SISTEMELOR CU AJUTORUL ECUAŢIILOR DE STARE

Un sistem liniar, invariant în timp, poate fi reprezentat cu ajutorul unui set de ecuaţii diferenţiale de ordinul I În spaţiul stărilor, aceste ecuaţii pot fi scrise după cum urmează: unde: - u este vectorul mărimilor de intrare - x este vectorul variabilelor de stare - y este vectorul variabilelor de ieşire.

Exemplu Pentru un sistem de întârziere de ordinul II, cu polii caracterizaţi de pulsaţia naturală ωn = 1. 5 şi factorul de amortizare este ξ = 0. 2 , ecuaţiile de stare corespunzatoare sistemului pot fi reprezentate în MATLAB astfel: >> wn= 1. 5; >> z=0. 2; >> a=[0 1; -wn^2 – 2*z*wn]; >> b=[0; wn^2]; >> c=[1 0]; >> d=0;

Consideram un model al unui sistem liniar de ordin n descris de urmatoarea ecuaţie diferenţială: Un model de stare pentru acest sistem nu este unic, fiind dependent de alegerea unui set de variabile de stare.

O modalitate de alegere a unui set de variabile de stare, este urmatoarea:

vom rezolva pentru şi vom înlocui y şi derivatele sale prin variabilele de stare corespunzătoare, rezultând:

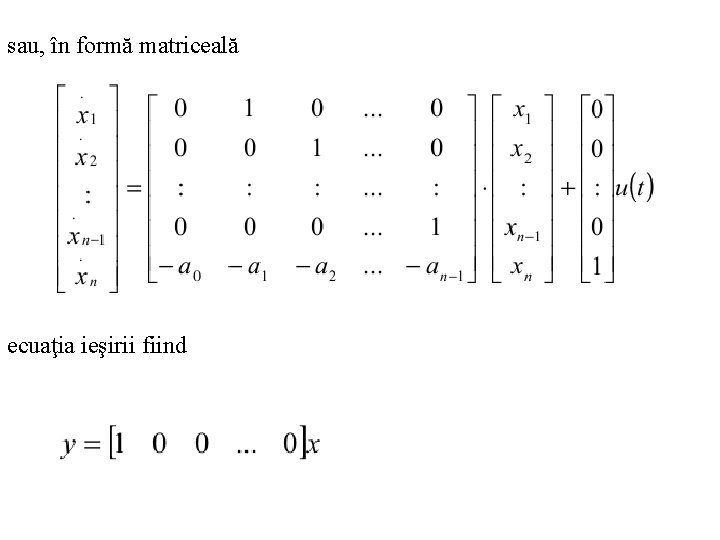
sau, în formă matriceală ecuaţia ieşirii fiind

Exemplul 1 Pentru sistemul descris de vom obţine

În descriere Matlab : >> ai=[2 4 6 8]; >> k=10; >> [A, B, C]=ode 2 phv(ai, k) A = [0 1 0; 0 0 1; -4 -3 -2] B = [0; 0; 5] C = [1 0 0]

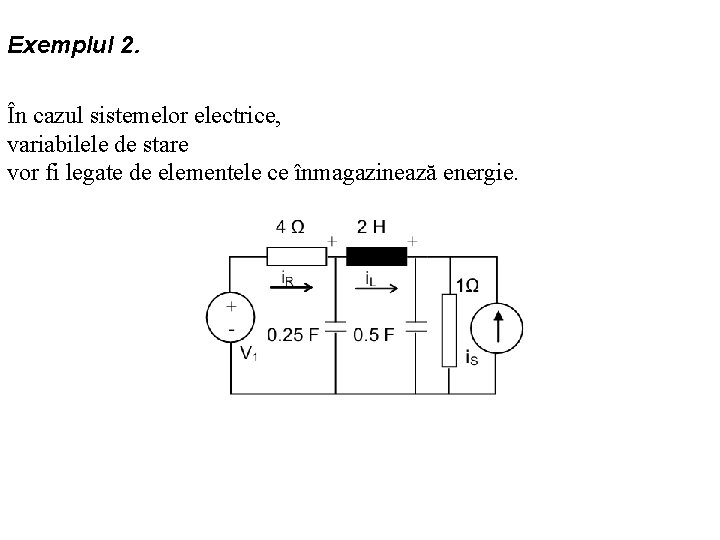
Exemplul 2. În cazul sistemelor electrice, variabilele de stare vor fi legate de elementele ce înmagazinează energie.

Ecuaţiile de funcţionare ale sistemului sunt:

Aceste ecuaţii pot fi scrise sub forma intrare-stare-ieşire, după cum urmează:

Exemplul 3 Conversia sistemului dat sub forma funcţiei de transfer în reprezentare în spaţiul stărilor. Fie sistemul cu funcţia de transfer :

>> num=[1 7 2]; >> den=[1 9 26 24]; >> [A, B, C, D]=tf 2 ss(num, den) A= -9 -26 -24 1 0 0 0 1 0 B= 1 0 0 C= 1 7 2 D= 0

Exemplul 4 Conversia spaţiul stărilor – funcţia de transfer Fie sistemul descris de ecuaţiile de stare:

>> A=[0 1 0; 0 0 1; -1 -2 -3]; >> B=[10; 0; 0]; >> C=[1 0 0]; >> D=[0]; >> [n, m]=ss 2 tf(A, B, C, D, 1) n= 0 10. 0000 30. 0000 20. 0000 m= 1. 0000 3. 0000 2. 0000 1. 0000 >> printsys(n, m) num/den = 10 s^2 + 30 s + 20 ----------s^3 + 3 s^2 + 2 s + 1

De asemenea, funcţia [z, p]=ss 2 tf(A, B, C, D, 1) poate converti ecuaţia de stare în funcţia de transfer sub forma factorizată (cu punerea în evidenţă a polilor şi zerourilor funcţiei de transfer)

>> [z, p]=ss 2 zp(A, B, C, D, 1) z= -2. 0000 -1. 0000 p= -2. 3247 -0. 3376 + 0. 5623 i -0. 3376 - 0. 5623 i