Sisteme de ecuatii liniare Prof FLORESCU NICOLAE GSIA

Sisteme de ecuatii liniare Prof. FLORESCU NICOLAE GSIA FETESTI

Notiuni generale Definitia 1: Sistemul (1) unde aij , bi ∈R , i ∈ {1, …, m}, j ∈{1, …, n} se numeste sistem de m ecuatii liniare cu n necunoscute. Definitia 2: Numerele reale x 1, x 2, x 3, … , xn care verifica fiecare ecuatie a sistemului (1) reprezinta solutia sistemului (1). A rezolva sistemul (1) inseamna a-i determina toate solutiile.

Definitia 3: Un sistem de ecuatii liniare care : Ø are solutie unica se numeste sistem compatibil determinat; Ø are o infinitate de solutii se numeste sistem compatibil nedeterminat; Ø nu are solutii se numeste sistem incompatibil. Definitia 4. Sistemul (1) se numeste omogen daca toti termenii liberi sunt egali cu zero.

Notatii Matricea se numeste matricea sistemului (1) Matricea se numeste matricea extinsa a sistemului (1).

se numeste matricea termenilor liberi se numeste matricea necunoscutelor Observatie: AX = B este forma matriceala a sistemului (1).

Rezolvarea matriceala a sistemelor liniare de n ecuatii cu n necunoscute Fie sistemul Etapa 1: -se scrie sistemul sub forma AX = B si se calculeaza det. A; Etapa 2: -daca det. A ≠ 0, se calculeaza A-1 ; Etapa 3: -solutia sistemului este X =A-1 B. Observatie: daca det. A = 0, atunci sistemul poate fi compatibil nedeterminat sau incompatibil. Exemplu: Sa se rezolve sistemul urmator utilizind metoda matriceala:

Sistemul dat se scrie astfel: Deci ,

Aplicatii 1. Utilizind metoda matriceala sa se rezolve sistemele: a). b). c). 2. Utilizind metoda matriceala , sa se rezolve sistemele urmatoare in functie de parametrul real m: a). b).

Metoda lui Cramer de rezolvare a sistemelor de n ecuatii cu n necunoscute Fie sistemul (1) Teorema: Daca pentru sistemul de ecuatii liniare (1) d = det. A ≠ 0 atunci sistemul este compatibil determinat , iar solutia este data de formulele (2) unde este determinantul obtinut din d prin inlocuirea coloanei i cu coloana termenilor liberi , celelalte coloane raminind neschimbate. Obs: 1). – in conditiile teoremei de mai sus , sistemul (1) se numeste sistem de tip Cramer; 2). – formulele (2) se numesc formulele lui Cramer.

Exemple 1. Sa se rezolve urmatorul sistem cu ajutorul regulii lui Cramer: Rezolvare: determinantul sistemului este = d= = = -10(-14 – 60) = 740 = 10

Pentru ca d ≠ 0 , sistemul este compatibil determinat. Avem: Deci, Solutia sistemului este S={(1, -2, 3 , 2 )}

2. Sa se arate ca sistemul are solutie unica daca si numai daca Rezolvare: determinantul sistemului este = -2αβγ Sistemul este compatibil determinat d≠ 0 αβγ ≠ 0. In acest caz solutia sistemului este data de formulele lui Cramer. Avem = = = Deci, , ,

Aplicatii 1. Sa se rezolve sistemele urmatoare utilizind regula lui Cramer: a). b). 2. Sa se determine parametrul real m astfel incit sistemele de mai jos sa aiba solutie unica: a). b). c).

Rezolvarea sistemelor de m ecuatii cu n necunoscute Fie sistemul (1). Teorema lui Kronecker-Capelli: Sistemul de ecuatii liniare (1) este compatibil daca si numai daca rang. A = rangĀ. Metoda de lucru: - fie rang. A = rangĀ = r - din rang. A = r in A minorul d = ≠ 0 numit minor principal

- necunoscutele ale caror coeficienti apar in d se numesc necunoscute principale; -ecuatiile ale caror coeficienti apar in d se numesc ecuatii principale; -necunoscutele ale caror coeficienti nu apar in d se numesc necunoscute secundare; lor li se vor atribui valori arbitrare ( , , etc. ). ; -rezulta un sistem de r ecuatii cu r necunoscute care se rezolva cu regula lui Cramer. Exemplu: 1. Sa se rezolve sistemul: Rezolvare: A= Ā= d= =0 , = 3 ≠ 0 si d este minor principal; deoarece =0 rang. A = 2 = 0 rangĀ = 2

deoarece rang. A = rangĀ sistemul este compatibil nedeterminat; x , y sint necunoscute principale z , t sint necunoscute secundare; notam z = , t = , unde , cu solutiile x =1 - - si y = 1 - Avem sistemul Solutia sistemului dat este 2. Rezolvati sistemul : Avem A = si Ā =

d= = 28 ≠ 0 rang. A = 3 iar d este minor principal = 14 ≠ 0 rangĀ = 4 Deoarece rang. A ≠ rangĀ sistemul este incompatibil. Observatie: In exemplul anterior se observa ca pentru a calcula rangul matricei Ā am bordat minorul principal cu elementele corespunzatoare coloanei termenilor liberi si elementele de pe linia ramasa in Ā. De aici deducem urmatoarea definitie: Definitie: Minorul obtinut prin bordarea minorului principal cu elementele corespunzatoare coloanei termenilor liberi si elementele corespunzatoare unei linii ramase in Ā se numeste minor caracteristic. Teorema lui Rouche: Un sistem de ecuatii liniare este compatibil toti minorii caracteristici sint nuli. Obs: metoda de determinare a solutiilor sistemului este cea descrisa la teorema lui Kronecker- Capelli.

Aplicatii 1. Sa se rezolve sistemul Rezolvare: avem d= = -5≠ 0 si , , Deci d este minor principal. Minorii caracteristici sint: si , deci sistemul este compatibil. Avem: x 1 , x 2 necunoscute principale si x 3 , x 4 necunoscute secundare. Notam x 3 = , x 4 = . Avem sistemul de tip Cramer Cu solutiile x 1 = -2 - + si x 2 = 3 + - . Solutia generala a sistemului dat este:

2. Sa se determine si astfel incit urmatoarele sisteme sa fie compatibile a). b). Rezolvare: a). A = Avem d= si Ā = = 6 ≠ 0 iar si rang. A = 2 iar d este minor principal. Sistemul este compatibil toti minorii caracteristici sint nuli. Exista un singur minor caracteristic, deci trebuie sa avem -4=0 = 4. b). A= ; Ā=

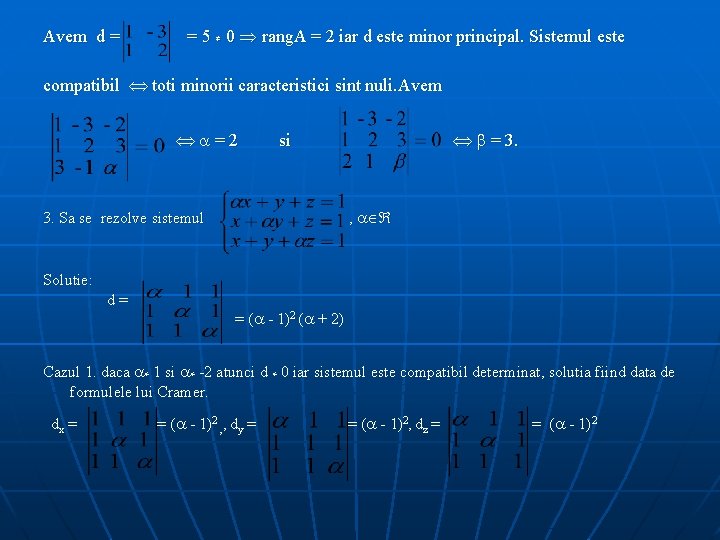
Avem d = = 5 ≠ 0 rang. A = 2 iar d este minor principal. Sistemul este compatibil toti minorii caracteristici sint nuli. Avem =2 = 3. si , 3. Sa se rezolve sistemul Solutie: d= = ( - 1)2 ( + 2) Cazul 1. daca ≠ 1 si ≠ -2 atunci d ≠ 0 iar sistemul este compatibil determinat, solutia fiind data de formulele lui Cramer. dx = = ( - 1)2 , , dy = = ( - 1)2, dz = = ( - 1)2

solutia sistemului este x = y = z = Cazul 2. daca = 1 , sistemul se reduce la ecuatia x + y + z = 1 iar solutia sistemului este x = 1 - - , y = , z = unde , Cazul 3. daca = -2 avem sistemul d = 0 si minorul = 3 ≠ 0 este minor principal. Singurul minor caracteristic este = 9 ≠ 0 deci sistemul este incompatibil.

Aplicatii 1. a). Sa se rezolve sistemele urmatoare: b). c). 2. Sa se rezolve si sa se discute dupa valorile parametrilor reali m si n sistemele: a). b).

Sisteme de ecuatii liniare omogene Sistemul se numeste sistem omogen. Observatii: 1. – un sistem omogen este intotdeauna compatibil ( intotdeauna rang. A = rangĀ, deci conform teoremei lui Kronecker – Capelli sistemul este compatibil); 2. – daca rang. A = r atunci avem urmatoarele situatii: a). pentru r = n singura solutie a sistemului omogen este solutia nula; b). pentru r < n sistemul are si solutii nenule ; se utilizeaza metodele invatate anterior pentru determinarea solutiilor sistemului. 3. –daca m = n atunci sistemul are solutii nenule det. A = 0; 4. –daca m < n atunci sistemul are solutii nenule. Exemplu: Sa se determine astfel incit sistemul urmator sa aiba solutii nenule si , in acest caz sa se rezolve:

= … = - d= Cazul 1. daca ≠ 0 sistemul are solutia unica x = y =z = t = 0 ; Cazul 2. daca = 0 sistemul are solutii nenule; in acest caz avem sistemul Minorul d’ = = -3 ≠ 0 este principal;

- x , y , z sint necunoscute principale t = - necunoscuta secundara; avem de rezolvat sistemul de tip Cramer Solutia este x = , y= , z = 3 Deci , pentru = 0 solutia generala a sistemului omogen dat este:

Aplicatii 1. Sa se rezolve sistemele urmatoare: a). b). c). 2. Se considera sistemul a). Sa se determine parametrul real m astfel incit sistemul sa aiba solutie unica. . b). Pentru m = 1 determinati solutia sistemului.