CURS 11 Rezolvarea ecuaiilor transcendente Fie ecuatia fx0

CURS 11 Rezolvarea ecuaţiilor transcendente Fie ecuatia: f(x)=0 algebrică - dacă poate fi adusă la o formă polinomială transcendentă – dacă nu este algebrică Ecuaţii algebrice: Ecuaţii transcendente: 3 x=9; sin(x)+cos(x)=0. 5; 2 x 2 -3 x+2=0; eln(x)-x=π; x 5=x(2 x-1); Pentru determinarea soluţiilor ecuaţiilor transcendente este nevoie de metode de aproximare. Rădăcină unei ecuatii: Cum se defineste o rădăcină aproximativă?

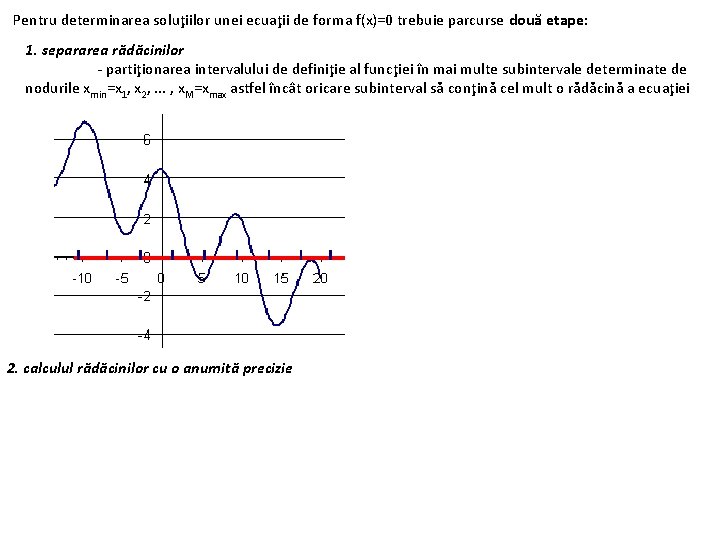
Pentru determinarea soluţiilor unei ecuaţii de forma f(x)=0 trebuie parcurse două etape: 1. separarea rădăcinilor - partiţionarea intervalului de definiţie al funcţiei în mai multe subintervale determinate de nodurile xmin=x 1, x 2, . . . , x. M=xmax astfel încât oricare subinterval să conţină cel mult o rădăcină a ecuaţiei 2. calculul rădăcinilor cu o anumită precizie

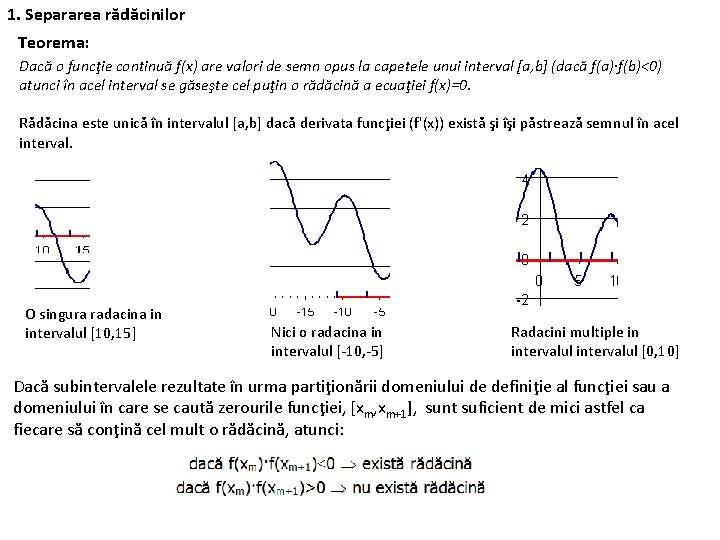
1. Separarea rădăcinilor Teorema: Dacă o funcţie continuă f(x) are valori de semn opus la capetele unui interval [a, b] (dacă f(a)·f(b)<0) atunci în acel interval se găseşte cel puţin o rădăcină a ecuaţiei f(x)=0. Rădăcina este unică în intervalul [a, b] dacă derivata funcţiei (f'(x)) există şi îşi păstrează semnul în acel interval. O singura radacina in intervalul [10, 15] Nici o radacina in intervalul [-10, -5] Radacini multiple in intervalul [0, 10] Dacă subintervalele rezultate în urma partiţionării domeniului de definiţie al funcţiei sau a domeniului în care se caută zerourile funcţiei, [xm, xm+1], sunt suficient de mici astfel ca fiecare să conţină cel mult o rădăcină, atunci:

2. Calculul rădăcinilor cu o anumită precizie Metode: - metoda bisecţiei (înjumătăţirii intervalului) - metoda lui Newton (metoda tangentei) - metoda secantei - metoda falsei poziţii -metoda aproximaţiilor succesive -. . .

Metoda bisecţiei - constă în împărţirea repetată a intervalului iniţial [a, b] în jumătăţi ale acestuia şi selectarea intervalului (jumătăţii) în care se află soluţia.

Conditia de oprire a procesului iterativ :

Avantaje si dezavantaje - oferă convergenţă liniară a soluţiei ecuaţiei - convergenţă lentă - garantează convergenţa la soluţia exactă dacă valorile f(a) şi f(b) sunt de semne contrare

Program exemplu: metoda bisecţiei //metoda bisectiei #include<stdio. h> #include<math. h> #include <conio. h> #include <stdlib. h> #define eps 1 e-8 double f(double x) { return 4. 5*cos(x/3)-x/4; } double bisect(double inf, double sup, double (*pf)(double)) { double c; if((*pf)(inf)==0) return inf; if((*pf)(sup)==0) return sup; if((*pf)(inf)*(*pf)(sup)>0) { printf("n. Nu exista sol sau exista solutii multiple"); while(!_kbhit()); exit(1); } do { c=(inf+sup)/2. 0; if((*pf)(c)==0) return c; if((*pf)(inf)*(*pf)(c)<0) sup=c; else inf=c; } while((sup-inf) >= eps); // conditia de oprire return c; } int main() { double s; float A=3. 0, B=4; s=bisect(A, B, f); printf("n. Solutia este s= %lfa", s); while(!_kbhit()); return 0; }

Metoda lui Newton - propusă de către Isaac Newton în anul 1669 - revăzută de către Joseph Raphson în 1690 si Thomas Simpson în 1740 - una dintre cele mai răspândite metode folosite în acest scop - algoritmul bazat pe această metodă poate fi folosit şi la determinarea minimului sau maximului unei funcţii prin determinarea zeroului primei derivate a funcţiei, în metode de optimizare. Fie ecuatia: f(x)=0

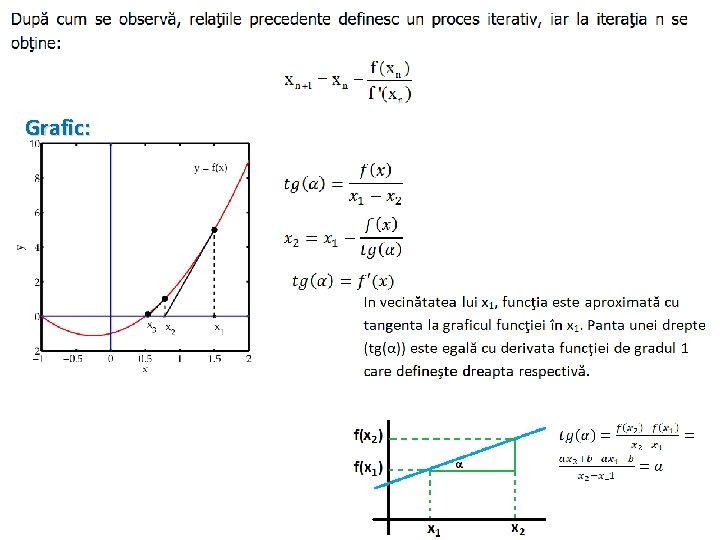
Grafic:

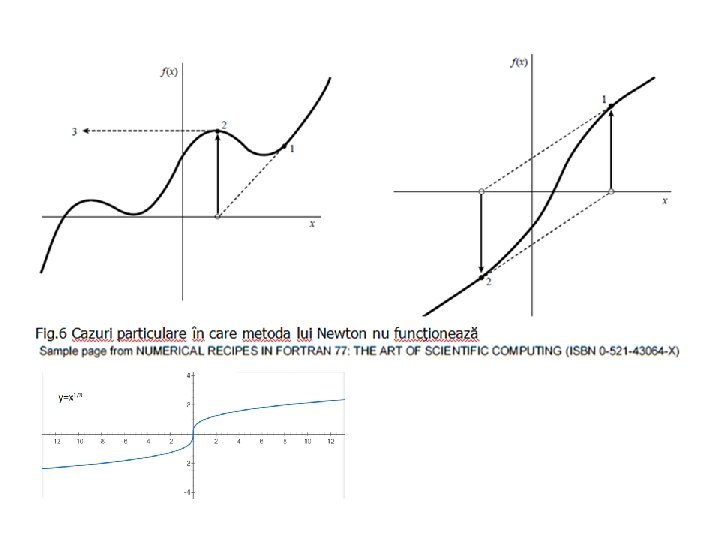
Conditia de oprire a procesului iterativ : Calculul soluţiei exacte implică: 1. alegerea unei aproximaţii iniţiale (x 0) a soluţiei ecuaţiei f(x)=0 - condiţie necesară şi suficientă: f(x 0)f"(x 0)>0. 2. calculul derivatei funcţiei al cărui zero se calculează - calcul numeric (daca nu este posibil analitic) Deoarece în relaţia iterativă de calcul a rădăcinii valoarea f'(x 0) apare la numitor, în cazul accidental în care derivata funcţiei în punctul xi este zero, se va alege pentru aceasta valoarea ε (o valoare mică, diferită de zero) folosită la calculul derivatei sale. Dezavantajele metodei lui Newton 1. în unele cazuri este necesară o alegere atentă a valorii de start, x 0 2. necesită evaluarea a două funcţii. 3. la o iteraţie, se poate determina numai una dintre rădăcinile ecuaţiei cu rădăcini multiple (depinde de rădăcina aproximativă de "guess" de la care se porneşte)

Calculul numeric al derivatelor 1. Forward differences method (FDM) 2. Central differences method (CDM)

Pentru valori de tip REAL, stocate pe 4 octeţi, p 10 -7, iar pentru valori de tip DOUBLE, stocate pe 8 octeţi, p 10 -16. Vezi cursul 2 – pasul de reprezentare a numerelor reale simpla precizie: 2 -23 = 1. 192 x 10 -7 dubla precizie: 2 -52= 2. 22 x 10 -16 Conditii pentru alegerea valorii

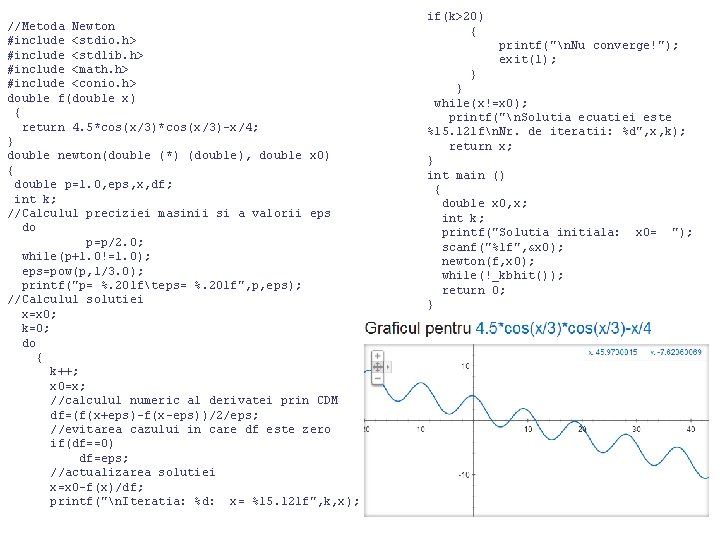
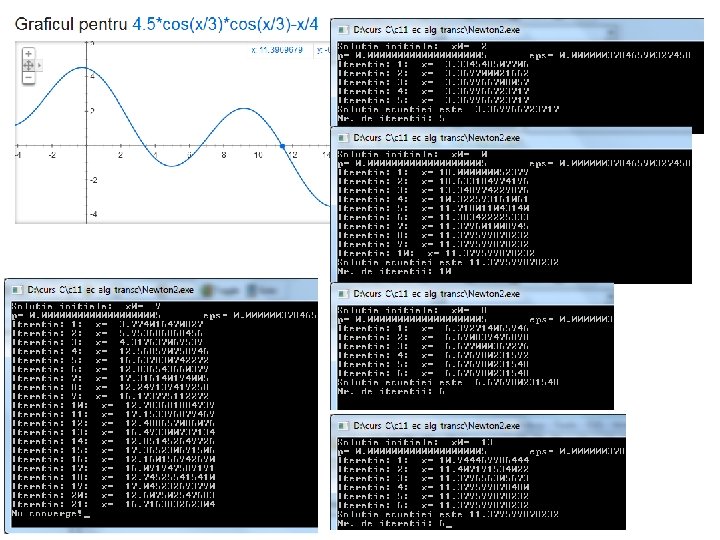
//Metoda Newton #include <stdio. h> #include <stdlib. h> #include <math. h> #include <conio. h> double f(double x) { return 4. 5*cos(x/3)-x/4; } double newton(double (*) (double), double x 0) { double p=1. 0, eps, x, df; int k; //Calculul preciziei masinii si a valorii eps do p=p/2. 0; while(p+1. 0!=1. 0); eps=pow(p, 1/3. 0); printf("p= %. 20 lfteps= %. 20 lf", p, eps); //Calculul solutiei x=x 0; k=0; do { k++; x 0=x; //calculul numeric al derivatei prin CDM df=(f(x+eps)-f(x-eps))/2/eps; //evitarea cazului in care df este zero if(df==0) df=eps; //actualizarea solutiei x=x 0 -f(x)/df; printf("n. Iteratia: %d: x= %15. 12 lf", k, x); if(k>20) { printf("n. Nu converge!"); exit(1); } } while(x!=x 0); printf("n. Solutia ecuatiei este %15. 12 lfn. Nr. de iteratii: %d", x, k); return x; } int main () { double x 0, x; int k; printf("Solutia initiala: x 0= "); scanf("%lf", &x 0); newton(f, x 0); while(!_kbhit()); return 0; }

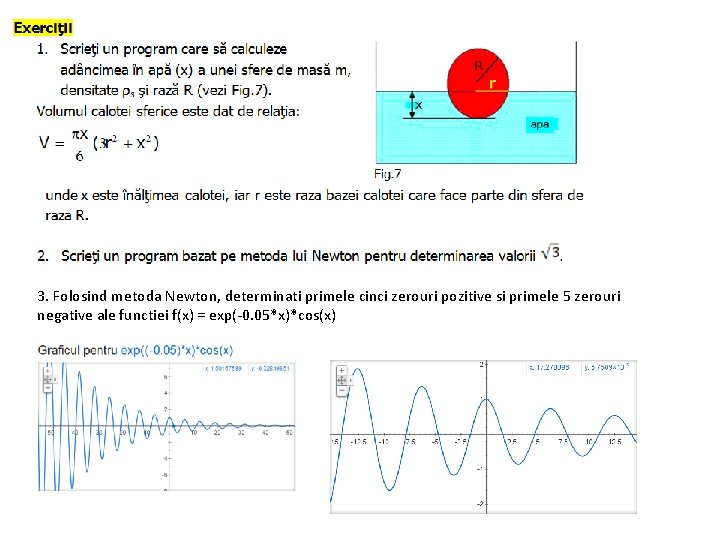
3. Folosind metoda Newton, determinati primele cinci zerouri pozitive si primele 5 zerouri negative ale functiei f(x) = exp(-0. 05*x)*cos(x)