Recovering metric and affine properties from images Parallelism



















- Slides: 30

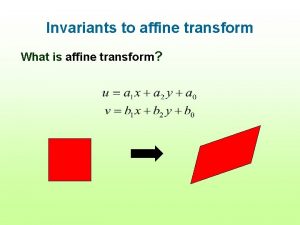
Recovering metric and affine properties from images • Parallelism • Parallel length ratios • Angles • Length ratios Will show: • Projective distortion can be removed once image of line at infinity is specified • Affine distortion removed once image of circular points is specified • Then the remaining distortion is only similarity

The line at infinity For an affine transformation line at infinity maps onto line at infinity The line at infinity l is a fixed line under a projective transformation H if and only if H is an affinity A point on line at infinity is mapped to ANOTHER point on the line at infinity, not necessarily the same point Note: not fixed pointwise

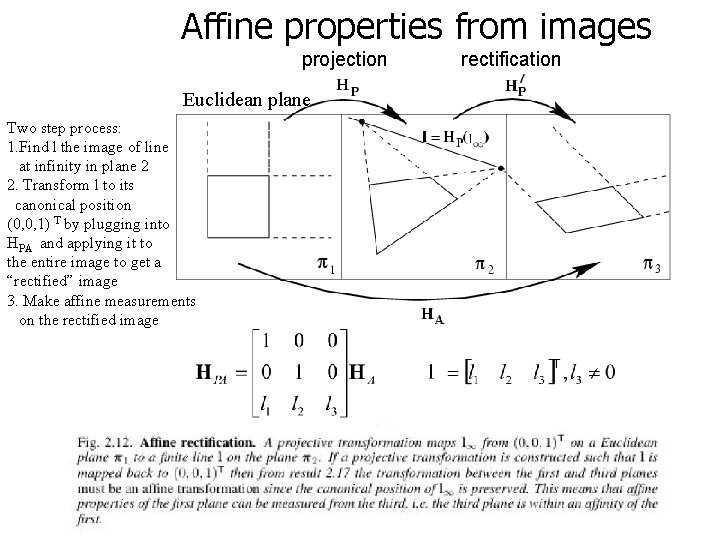
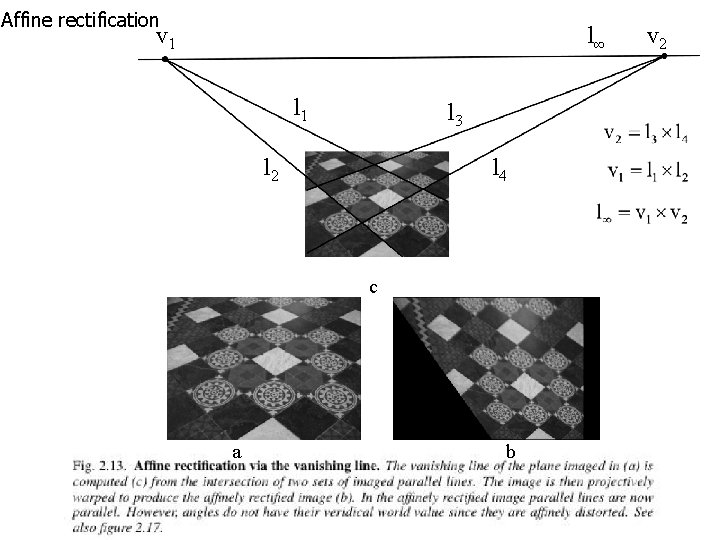
Affine properties from images projection Euclidean plane Two step process: 1. Find l the image of line at infinity in plane 2 2. Transform l to its canonical position (0, 0, 1) T by plugging into HPA and applying it to the entire image to get a “rectified” image 3. Make affine measurements on the rectified image rectification

Affine rectification l∞ v 1 l 3 l 2 l 4 c a b v 2

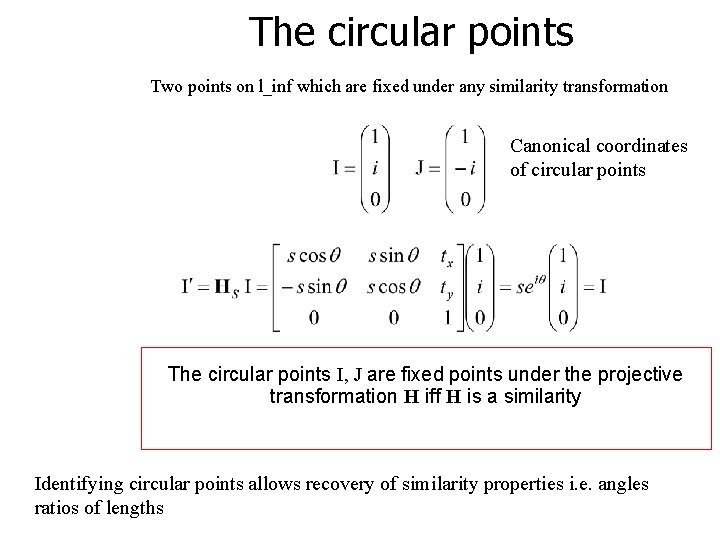
The circular points Two points on l_inf: Every circle intersects l_inf at circular points “circular points” Circle: Line at infinity Algebraically, encodes orthogonal directions l∞

The circular points Two points on l_inf which are fixed under any similarity transformation Canonical coordinates of circular points The circular points I, J are fixed points under the projective transformation H iff H is a similarity Identifying circular points allows recovery of similarity properties i. e. angles ratios of lengths

Conic dual to the circular points The dual conic is fixed conic under the projective transformation H iff H is a similarity Note: has 4 DOF (3 x 3 ho mogeneous; symmetric, determinant is zero) l∞ is the nullvector

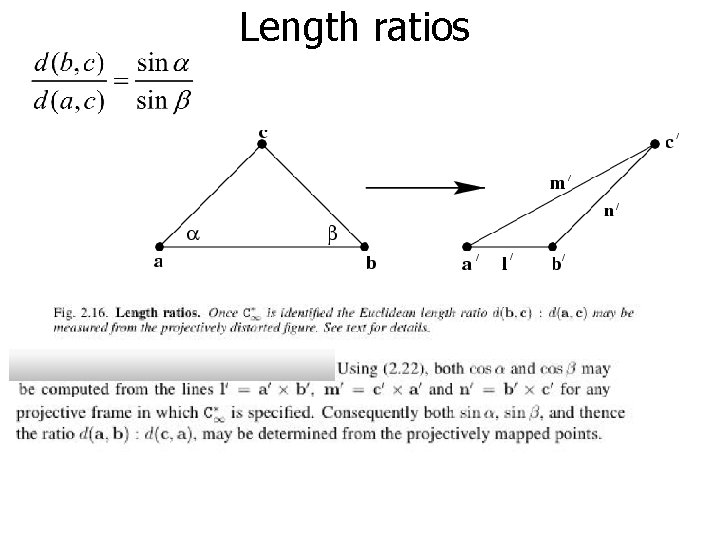
Angles Euclidean: Projective: (orthogonal) Once is identified in the projective plane, then Euclidean angles may be measured by equation (1)

Length ratios

Metric properties from images • Upshot: projective (v) and affine (K) components directly determined from the image of C*∞ • Once C*∞ is identified on the projective plane then projective distortion may be rectified up to a similarity Rectifying transformation from SVD

Metric from affine Affine rectified

Metric from projective

Projective 3 D geometry

Singular Value Decomposition

Singular Value Decomposition • Homogeneous least-squares • Span and null-space • Closest rank r approximation • Pseudo inverse

Projective 3 D Geometry • Points, lines, planes and quadrics • Transformations • П∞, ω∞ and Ω ∞

3 D points 3 D point in R 3 in P 3 projective transformation (4 x 4 -1=15 dof)

Planes 3 D plane Euclidean representation Dual: points ↔ planes, lines ↔ lines Transformation

Planes from points (solve as right nullspace of Or implicitly from coplanarity condition )

Points from planes (solve as right nullspace of Representing a plane by its span • M is 4 x 3 matrix. Columns of M are null space of • X is a point on plane • x ( a point on projective plane P 2 ) parameterizes points on the plane π • M is not unique )

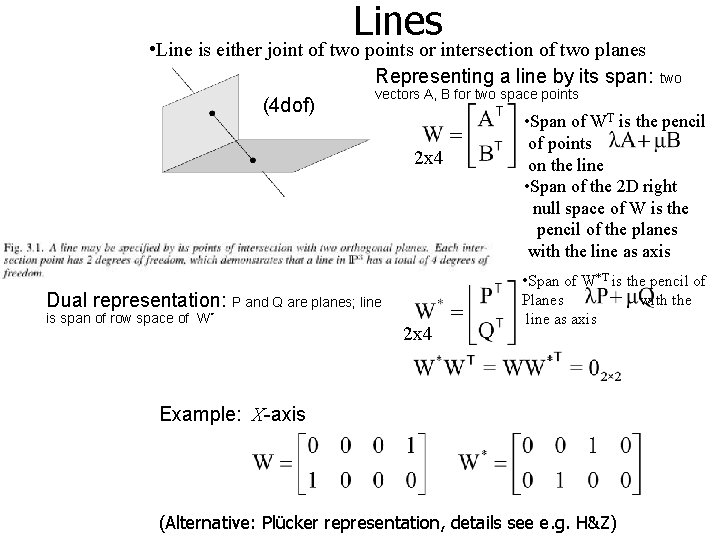
Lines • Line is either joint of two points or intersection of two planes Representing a line by its span: two vectors A, B for two space points (4 dof) T 2 x 4 Dual representation: P and Q are planes; line is span of row space of W* 2 x 4 • Span of W is the pencil of points on the line • Span of the 2 D right null space of W is the pencil of the planes with the line as axis • Span of W*T is the pencil of Planes with the line as axis Example: X-axis (Alternative: Plücker representation, details see e. g. H&Z)

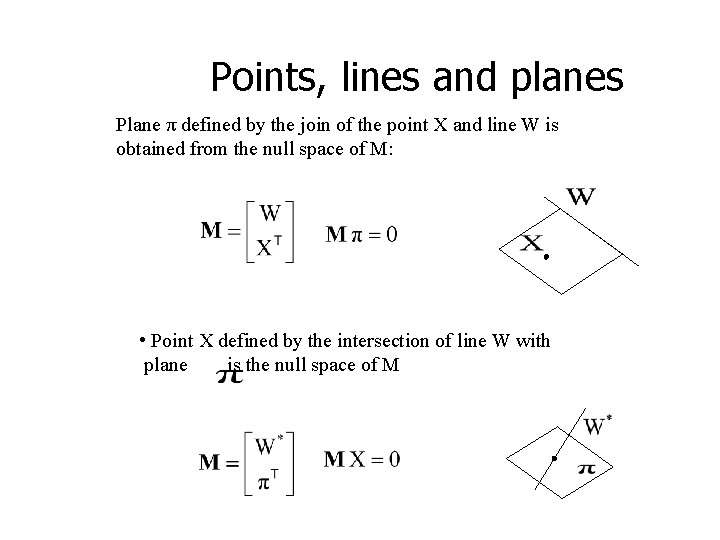
Points, lines and planes Plane π defined by the join of the point X and line W is obtained from the null space of M: • Point X defined by the intersection of line W with plane is the null space of M

Quadrics and dual quadrics Quadratic surface in P 3 defined by: (Q : 4 x 4 symmetric matrix) 1. 2. 3. 4. 5. 6. 9 d. o. f. in general 9 points define quadric det Q=0 ↔ degenerate quadric pole – polar (plane ∩ quadric)=conic transformation • Dual Quadric: defines equation on planes: tangent planes π to the point quadric Q satisfy: 1. 2. relation to quadric transformation (non-degenerate)

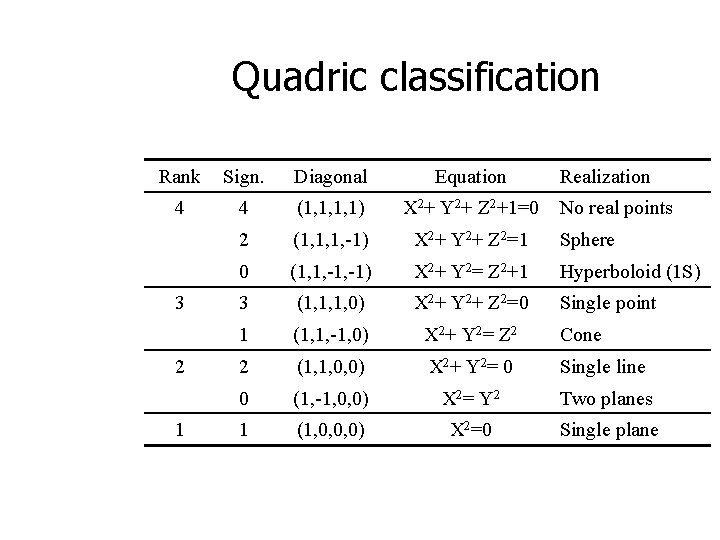
Quadric classification Rank Sign. Diagonal Equation 4 4 (1, 1, 1, 1) X 2+ Y 2+ Z 2+1=0 2 (1, 1, 1, -1) X 2+ Y 2+ Z 2=1 Sphere 0 (1, 1, -1) X 2+ Y 2= Z 2+1 Hyperboloid (1 S) 3 (1, 1, 1, 0) X 2+ Y 2+ Z 2=0 Single point 1 (1, 1, -1, 0) X 2 + Y 2 = Z 2 Cone 2 (1, 1, 0, 0) X 2 + Y 2 = 0 Single line 0 (1, -1, 0, 0) X 2 = Y 2 Two planes 1 (1, 0, 0, 0) X 2=0 Single plane 3 2 1 Realization No real points

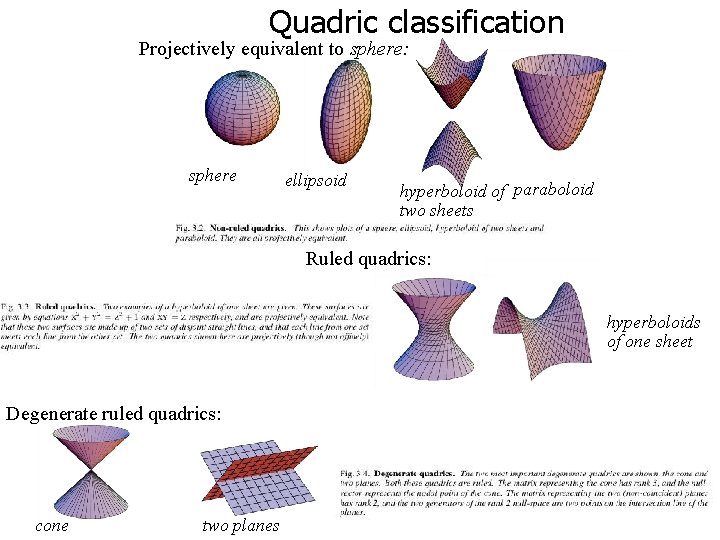
Quadric classification Projectively equivalent to sphere: sphere ellipsoid hyperboloid of paraboloid two sheets Ruled quadrics: hyperboloids of one sheet Degenerate ruled quadrics: cone two planes

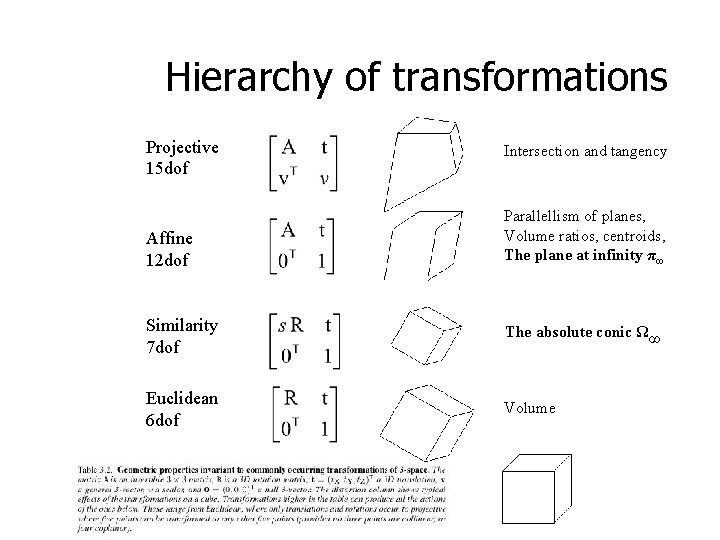
Hierarchy of transformations Projective 15 dof Affine 12 dof Intersection and tangency Parallellism of planes, Volume ratios, centroids, The plane at infinity π∞ Similarity 7 dof The absolute conic Ω∞ Euclidean 6 dof Volume

The plane at infinity π is a fixed plane under a projective transformation H iff H is an affinity 1. 2. 3. 4. canical position contains directions two planes are parallel line of intersection in π∞ line // line (or plane) point of intersection in π∞

The absolute conic Ω∞ is a (point) conic on π. In a metric frame: The absolute conic Ω∞ is a fixed conic under the projective transformation H iff H is a similarity 1. 2. 3. Ω∞ is only fixed as a set, not pointwise Circle intersect Ω∞ in two points All Spheres intersect π∞ in Ω∞

The absolute conic Euclidean: Projective: (orthogonality=conjugacy) d 1 and d 2 are lines

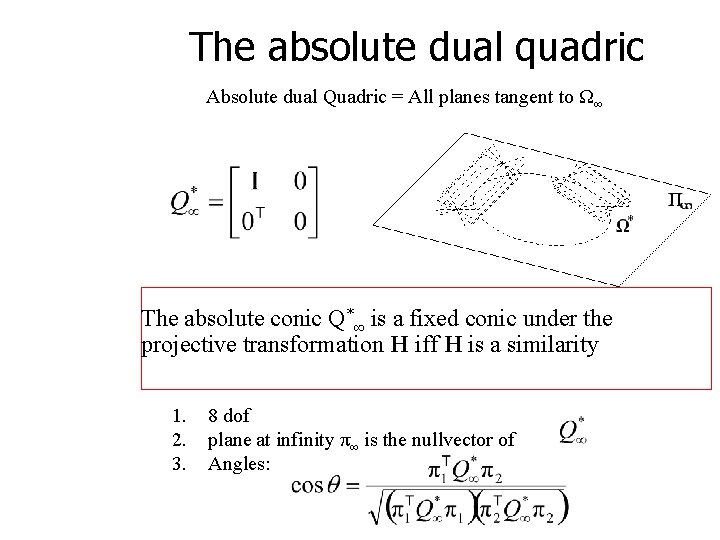
The absolute dual quadric Absolute dual Quadric = All planes tangent to Ω∞ The absolute conic Q*∞ is a fixed conic under the projective transformation H iff H is a similarity 1. 2. 3. 8 dof plane at infinity π∞ is the nullvector of Angles:
 Thread-level parallelism
Thread-level parallelism Middlesbrough recovering together
Middlesbrough recovering together Metric mania
Metric mania Affine transformation examples
Affine transformation examples Affine gap penalty
Affine gap penalty Brute force attack on affine cipher
Brute force attack on affine cipher Affine gap distance
Affine gap distance Fonction affine
Fonction affine Hassan javaid
Hassan javaid Warp affine
Warp affine Glissosimmetria equazione
Glissosimmetria equazione Equiarea
Equiarea Exemple de fonction dans la vie courante
Exemple de fonction dans la vie courante Affines koordinatensystem
Affines koordinatensystem Atbash
Atbash Decipher the message
Decipher the message Affine combination
Affine combination Pigpen
Pigpen Affine image warping
Affine image warping Metric measurement images
Metric measurement images Distance properties
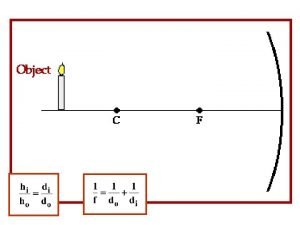
Distance properties Real image vs virtual
Real image vs virtual Real image concave mirror
Real image concave mirror Mail @ malaysia.images.search.yahoo.com
Mail @ malaysia.images.search.yahoo.com How to save images on google images
How to save images on google images Yahoo.com.yw
Yahoo.com.yw Extensive vs intensive properties
Extensive vs intensive properties Physical and chemical properties
Physical and chemical properties Salt acronym mirrors
Salt acronym mirrors Syntactical parallelism
Syntactical parallelism Parallelism coordination subordination division
Parallelism coordination subordination division