Reconstruction on trees and Phylogeny 3 Elchanan Mossel

Reconstruction on trees and Phylogeny 3 Elchanan Mossel, U. C. Berkeley mossel@stat. berkeley. edu, http: //www. cs. berkeley. edu/~mossel/ Supported by Microsoft Research and the Miller Institute 12/23/2021 1

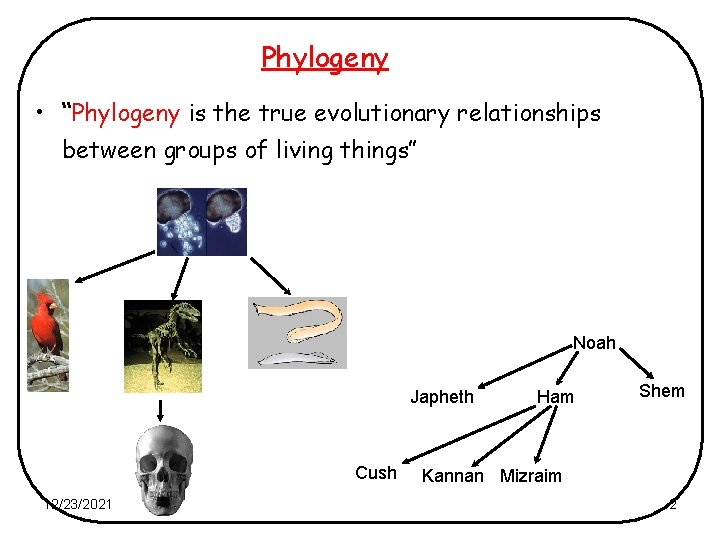
Phylogeny • “Phylogeny is the true evolutionary relationships between groups of living things” Noah Japheth Cush 12/23/2021 Ham Shem Kannan Mizraim 2

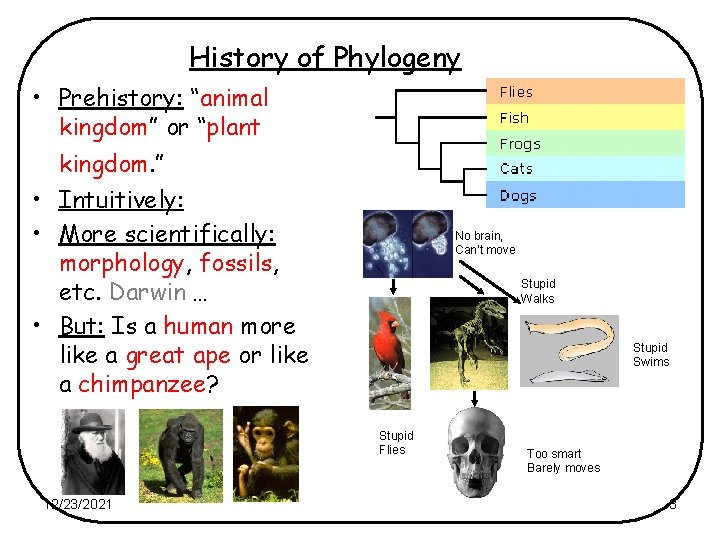
History of Phylogeny • Prehistory: “animal kingdom” or “plant kingdom. ” • Intuitively: • More scientifically: morphology, fossils, etc. Darwin … • But: Is a human more like a great ape or like a chimpanzee? No brain, Can’t move Stupid Walks Stupid Swims Stupid Flies 12/23/2021 Too smart Barely moves 3

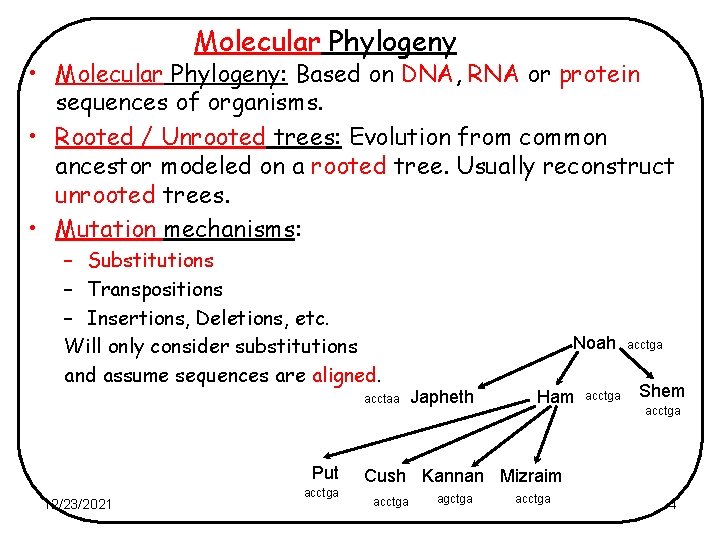
Molecular Phylogeny • Molecular Phylogeny: Based on DNA, RNA or protein sequences of organisms. • Rooted / Unrooted trees: Evolution from common ancestor modeled on a rooted tree. Usually reconstruct unrooted trees. • Mutation mechanisms: – Substitutions – Transpositions – Insertions, Deletions, etc. Will only consider substitutions and assume sequences are aligned. acctaa Put 12/23/2021 acctga Noah Japheth Ham acctga Shem acctga Cush Kannan Mizraim acctga agctga acctga 4

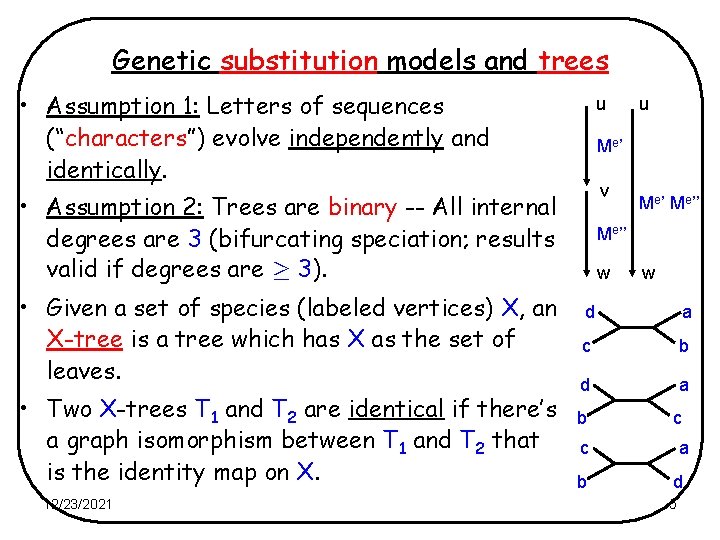
Genetic substitution models and trees • Assumption 1: Letters of sequences (“characters”) evolve independently and identically. u Me ’ v • Assumption 2: Trees are binary -- All internal degrees are 3 (bifurcating speciation; results valid if degrees are ¸ 3). • Given a set of species (labeled vertices) X, an X-tree is a tree which has X as the set of leaves. • Two X-trees T 1 and T 2 are identical if there’s a graph isomorphism between T 1 and T 2 that is the identity map on X. 12/23/2021 u Me’’ w w d a c b d a b c c a b d 5

• • Substitution model – finite state space Finite set A of information values (|A| = 4 for DNA). Tree T=(V, E) rooted at r. Vertex v 2 V, has information σv 2 A. Edge e=(v, u), where v is the parent of u, has a mutation matrix Me of size |A| £ |A|: Mi, j (v, u) = P[ u = j | v = i] Will focus on the CFN model: A character is ( v)v 2 T. For each character , the data is T = ( v)v 2 T, where T is the boundary of the tree; | T| = n. • We are given k independent characters 1 T, …, k T. 12/23/2021 6

A diagram Length of sequence! • Interested to know k = #characters needed to reconstruct the tree with n = #leaves, given a range [ max, min] for mutation rate . 12/23/2021 7

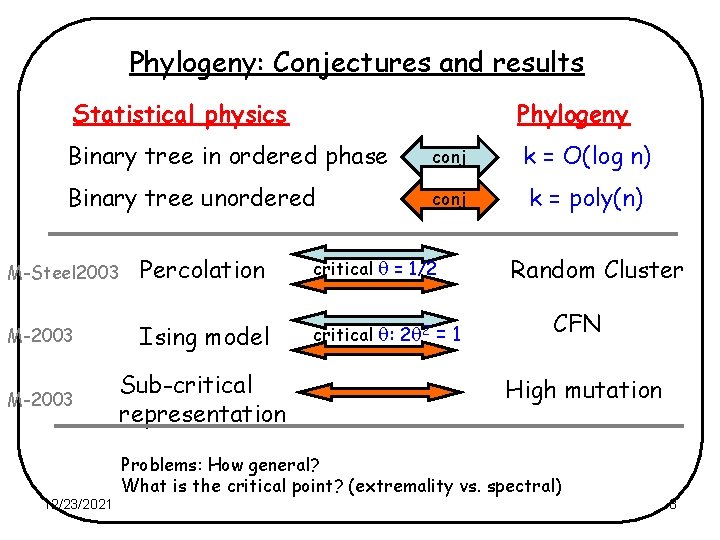
Phylogeny: Conjectures and results Statistical physics Phylogeny Binary tree in ordered phase conj k = O(log n) Binary tree unordered conj k = poly(n) M-Steel 2003 Percolation critical = 1/2 M-2003 Ising model critical : 2 2 = 1 M-2003 Sub-critical representation 12/23/2021 Random Cluster CFN High mutation Problems: How general? What is the critical point? (extremality vs. spectral) 8

The CFN model • Cavendar-Farris-Neyman model: – 2 data types: 1 and – 1 (“purine-pyrimidine”) – Mutation along edge e: with probability (e) copy data from parent. Otherwise, choose 1/-1 with probability ½ independently of everything else Thm[CFN] Suppose that for all e, 1 - > (e) > > 0. Then given k characters of the process at n leaves, It is possible to reconstruct the underlying topology with probability 1 - , if k = n. O(-log ). 12/23/2021 Steel 94: Trick to extend to general Me provided that det(Me) [-1, -1+ ] [- , ] [1 - , 1], 9

Phase transition for the CFN model • Th 1[M 2003]: Suppose that n=3 £ 2 q and - T is a uniformly chosen (q+1)-level 3 -regular X-tree. – For all e, (e) < , and 2 2 < 1. – Then in order to reconstruct the topology with probability > 0. 1, at least k = (n(-2 log 2( ) - 1)) characters are needed. • Proof: Information theoretic variant of the proof for random cluster model. • Same proof applies to any model for which the reconstruction problem is unsolvable. – more formally, for models for which I( , n) decays exp. fast in n. 12/23/2021 10

CFN Logarithmic reconstruction Th 2[M 2003]: If T is an X-tree on n leaves s. t. – For all e, min < (e)< max and 2 2 min > 1, max < 1. – Then k = O(log n – log ) characters suffice to reconstruct the topology with probability 1 - . – Need either a “balanced tree” – all leaves at the same distance from a root. – Or, “molecular clock” – (e) = e-t(e), where t(e) is the time interval between the two endpoints of the interval + all leaves are at the same time. 12/23/2021 11

Main Lemma [M 2003] • Lemma: Suppose that 2 min 2 > 1, then there exists an L, and > 0 such that the CFN model on the binary tree of L levels with – (e) min, for all e not adjacent to ∂T. – (e) min , for all e adjacent to ∂T. satisfies E[σr Maj(σ∂)] . • Roughly, given boundary data of “quality ”, we can reconstruct the root data with “quality ”. • In phylogeny – can treat known pieces of the tree as vertices. • Main problem: how to reconstruct pieces of the tree? 12/23/2021 12

Metric spaces on trees • Let D be a positive function on the edges E. • Define D(u, v) = {D(e) : e 2 path(u, v)}. • Claim: Given D(v, u) for all v and u in T, it is possible to reconstruct the topology of T. • Proof: Suffices to find d(u, v) for all u, v 2 T where d is the graph metric distance. • d(u 1, u 2) = 2 iff for all w 1 and w 2 it holds that D’(u 1, u 2, w 1, w 2) : = D(u 1, w 1)+D(u 2, w 2) –D(u 1, u 2)–D(w 1, w 2) ¸ 0 (“Four point condition”). u 1 u 2 12/23/2021 w 2 w 1 u 1 w 2 u 2 13

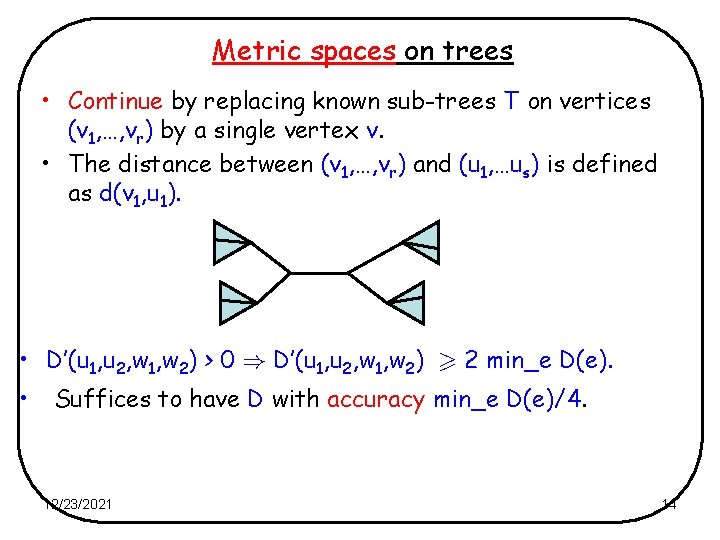
Metric spaces on trees • Continue by replacing known sub-trees T on vertices (v 1, …, vr) by a single vertex v. • The distance between (v 1, …, vr) and (u 1, …us) is defined as d(v 1, u 1). • D’(u 1, u 2, w 1, w 2) > 0 ) D’(u 1, u 2, w 1, w 2) 2 min_e D(e). • Suffices to have D with accuracy min_e D(e)/4. 12/23/2021 14

Metric spaces on trees • Let T be a balanced tree. • The L-topology of T is – d¤(u, v) : = min{d(u, v}, 2 L}. • Claim: If T is balanced, then in order to recover the L-topology of T it suffices to have – For each leaf u of T a set U(u) containing all elements at distance · 2 L+2 from u. – For all u and all w 1, w 2, w 3, w 4 2 U(u) the sign of D’(w 1, w 2, w 3, w 4). • “proof”: If d(u 1, u 2) > 2, then either – – u 2 is not in U(u 1), or Let v be a sister of u 1 and v’ a cousin of v. D’(u 1, v, u 2, v’) > 0. We have a witness that u 1 and u 2 are not siblings. u 2 12/23/2021 v’ v u 1 15

Proof of CFN theorem • Define D(e) = - log (e). • D(u, v) = -log(Cov( v, u)), where Cov( v, u) = E[ v u]. • Estimate Cov( v, u) by Cor( v, u) where • Need D with accuracy m = min D(e)/4 = c , or Cor = (1 c )Cov. • Cor( v, u) is a sum of k i. i. d. 1 variables with expected value Cov( v, u). • Cov( v, u) may be a small as 2 depth(T) = n-O(-log ). • Given k = nΩ(-log ) characters, it is possible to estimate D and therefore reconstruct T with high probability. 12/23/2021 16

Reconstructing the topology [M 2003] • The algorithm: Repeat the following: – Reconstruct the topology up to l levels from the boundary using 4 -points method. – For each sample, reconstruct the data l levels from the boundary using majority algorithm. + - - + • Reconstruction near the boundary take O(log n) samples. • By main lemma quality stays above . 12/23/2021 17

Proving main Lemma • Need to estimate E[σr Maj(σ∂)]. Estimate has two parts: • Case 1: For all e adjacent to ∂T, (e) is small. Here we use a perturbation argument, i. e. estimate partial derivatives of E[σr Maj(σ∂)] with respect to various variables (using something like Russo formula). • Case 2: Some e adjacent to ∂T has large (e). Use percolation theory arguments. • Both cases uses isoperimetric estimates for the discrete cube. 12/23/2021 18