On Sensitivity and Chaos Elchanan Mossel U C













![From Gaussian to discrete stability • A new limit theorem [M+O’Donnell+Oleszkiewicz]: • Let f From Gaussian to discrete stability • A new limit theorem [M+O’Donnell+Oleszkiewicz]: • Let f](https://slidetodoc.com/presentation_image_h2/584edb5196ef674e2cf54991b7badca9/image-24.jpg)







- Slides: 32

On Sensitivity and Chaos Elchanan Mossel, U. C. Berkeley mossel@stat. berkeley. edu, http: //www. stat. berkeley. edu/~mossel/ 1/6/2022 1

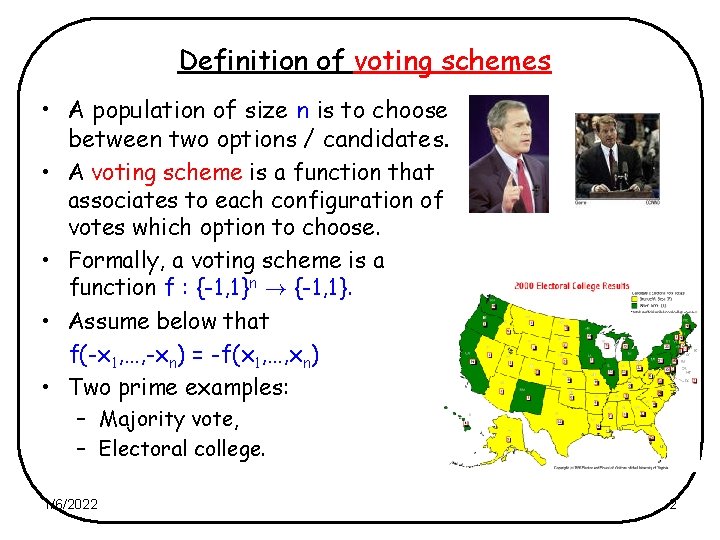
Definition of voting schemes • A population of size n is to choose between two options / candidates. • A voting scheme is a function that associates to each configuration of votes which option to choose. • Formally, a voting scheme is a function f : {-1, 1}n ! {-1, 1}. • Assume below that f(-x 1, …, -xn) = -f(x 1, …, xn) • Two prime examples: – Majority vote, – Electoral college. 1/6/2022 2

A mathematical model of voting • At the morning of the vote: • Each voter tosses a coin. • The voters want to vote according to the outcome of the coin. 1/6/2022 3

Ranking 3 candidates • Each voter tosses a dice. • Vote according to the corresponding order on A, B and C. 1/6/2022 4

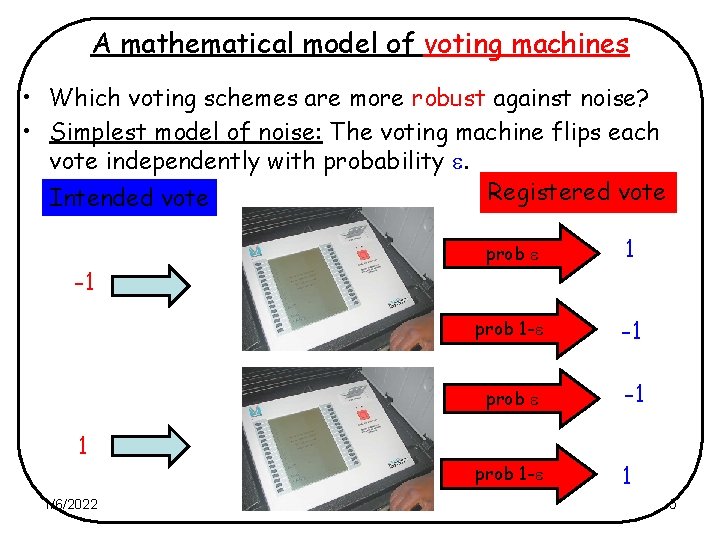
A mathematical model of voting machines • Which voting schemes are more robust against noise? • Simplest model of noise: The voting machine flips each vote independently with probability . Registered vote Intended vote -1 prob 1 - -1 prob -1 1 prob 1 - 1/6/2022 1 5

Formal model • Assume x is chosen uniformly in {-1, 1}n. • Let = 1 -2. • Let y = N (x) is obtained from x by flipping each of x coordinates with probability . • Equivalently: yi = xi with probability ; otherwise an independent coin-toss. • Question: What is the probability that the population voted for who they meant to vote for? • What is S (f) = E[f(x) f(N (x))]? • Which is the most sensitive / stable f? • Is there an f which is both stable and sensible? • Maj? Electoral college? 1/6/2022 6

Predicting the outcome of the elections • How many of the votes do we need to see to predict the outcome of the elections? • Let yi = 0 (unknown) with probability and yi = xi = § 1 with probability 1 -. • How large can V (f, ) = Py[ E[f(x) |y] > 1 - ] be for small ? 1/6/2022 7

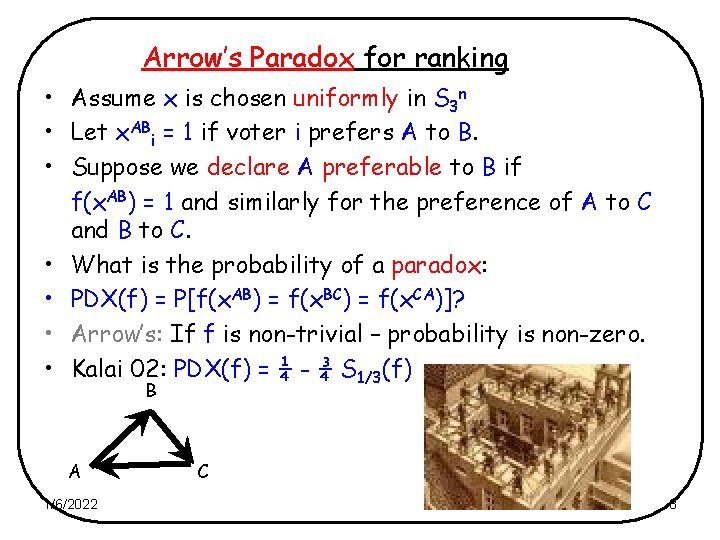
Arrow’s Paradox for ranking • Assume x is chosen uniformly in S 3 n • Let x. ABi = 1 if voter i prefers A to B. • Suppose we declare A preferable to B if f(x. AB) = 1 and similarly for the preference of A to C and B to C. • What is the probability of a paradox: • PDX(f) = P[f(x. AB) = f(x. BC) = f(x. CA)]? • Arrow’s: If f is non-trivial – probability is non-zero. • Kalai 02: PDX(f) = ¼ - ¾ S 1/3(f) B A 1/6/2022 C 8

Examples: majority & elec. college • It is easy to calculate that: • For f = Majority on n voters: limn ! 1 Er (f) = ½ - arcsin(1 – 2 )/ • When is small Er (f) » 2 1/2/. • Machine error ~ 0. 01% ) voting error ~ 1%. • Result is essentially due to Sheppard (1899!): “On the application of theory of error to cases of normal distribution and normal correlation” • An n 1/2 £ n 1/2 electoral college gives Er (f) = ( 1/4). • Machine error ~ 0. 01% ) voting error ~ 10%!. 1/6/2022 9

Some easy answers • Noise Theorem (folklore): Dictatorship, f(x) = xi is the most stable balanced voting scheme. • In other words, for all schemes: %(error in voting) ¸ %(error in machines) • Paradox Theorem (Arrow’s): • f(x) = xi minimizes the probability of a non-rational outcome. • Exit poll calculations: • For dictator we know the outcome with probability 1 -. 1/6/2022 10

Low influences and democracy • But in fact, we do not care about Dictators or Juntas • Want functions that depend on all (many) coordinates. • The influence of i’th variable of f : {-1, 1}n ! {-1, 1} is Ii(f) = P[f(x 1, …, xi, …, xn) f(x 1, …, -xi, …, xn)] • More generally for f : {-1, 1}n ! R let Ii(f) = i 2 S f. S 2. • Examples: Ii(f(x) = xj) = i, j, Ii(Maj) ~ n-1/2 • Notion introduced by Ben. Or-Linial, Later KKL … • From now on look at function with low influences – these are not determined by small # of coordinates. 1/6/2022 X X 11

Low influences and PCPs • Khot 02 suggested a paradigm for proving that problems are hard to approximate. • (Very) Roughly speaking the hardness of approximation factor is given by c/s where • c = lim ! 0 supn, f E[f(x) f(y) : 8 i, Ii(f) · , E[f] = a} • s = supn, f E[f(x) f(y) : E[f] = a} • x and y are correlated inputs. The correlation between them is related to the problem for which one wants to prove hardness. • It is not known if Khots paradigm is equivalent to classical NP hardness. • But the paradigm have given sharp hardness factors for many problems. 1/6/2022 12

Some Conjectures – now theorems • • Let I(f) = max Ii(f). Conj (Kalai-01) Thm: (M-O’Donnell-Oleskiewicz-05): For f with low influences – “it ain’t over until it’s over: ” As ! 1, ( ! 0 and ! 0): sup[V (f, ) : I(f) · , E[f] = 0. • Conj (Kalai-02) Thm: (M-O’Donnell-Oleskiewicz-05): • “The probability of an Arrow Paradox” • As ! 0 sup[PDX(f) : I(f) · , E[f] = 0] is minimized by the Majority function • Recall: PDX(f) = ¼ - ¾ S 1/3(f) 1/6/2022 13

Some Conjectures – now theorems • Conj (Khot-Kindler-M-O’Donnell-04) • Thm(M-O’Donnell-Oleskiewicz-05): “Majority is Stablest” • As ! 0 the quantity sup[S (f) : I(f) · , E[f] = 0] = (2 arcsin )/ is maximized by the majority function for all > 0. • Motivated by “MAX-CUT” (more later). • Thm (Dinur-M-Regev): “Large independent set” • Look at {0, 1, 2}n with edges between x and y if xi yi for all i. Then an independent set of size ¸ 10 -6 has an influencial variable. • Motivated by hardness of coloring. 1/6/2022 14

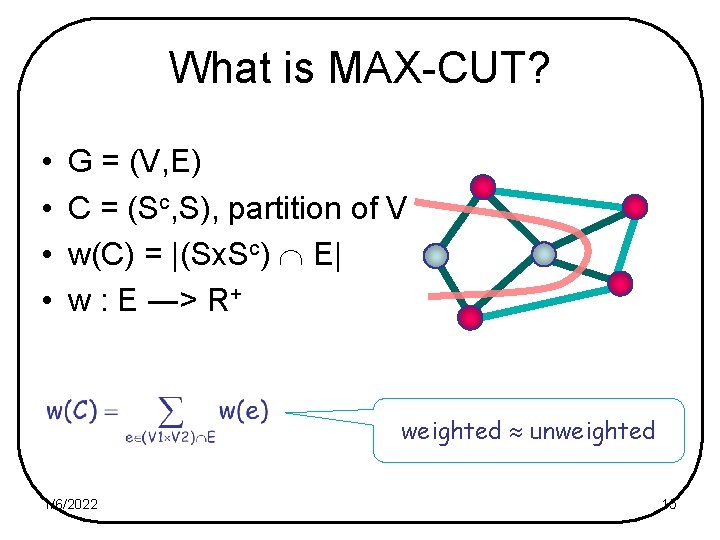
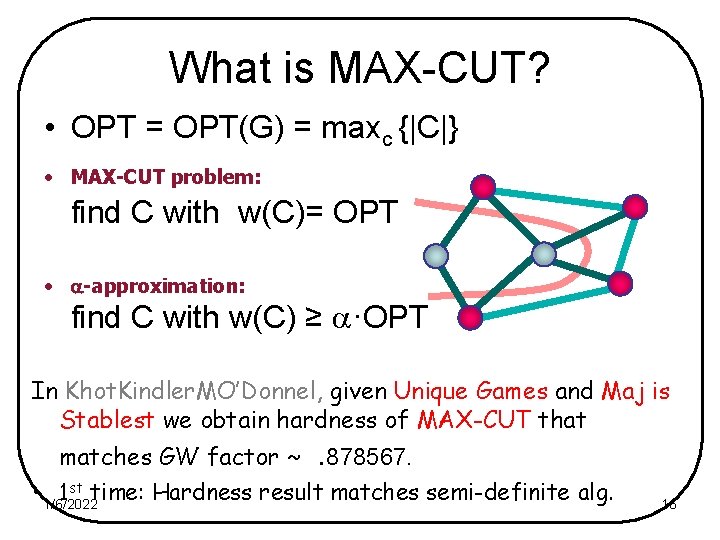
What is MAX-CUT? • • G = (V, E) C = (Sc, S), partition of V w(C) = |(Sx. Sc) E| w : E ―> R+ weighted unweighted 1/6/2022 15

What is MAX-CUT? • OPT = OPT(G) = maxc {|C|} • MAX-CUT problem: find C with w(C)= OPT • -approximation: find C with w(C) ≥ ·OPT In Khot. Kindler. MO’Donnel, given Unique Games and Maj is Stablest we obtain hardness of MAX-CUT that matches GW factor ~. 878567. • 1/6/2022 1 st time: Hardness result matches semi-definite alg. 16

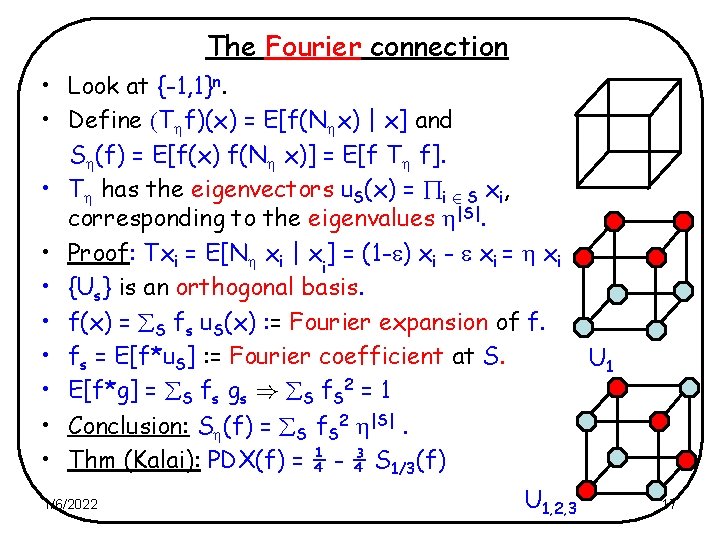
The Fourier connection • Look at {-1, 1}n. • Define (T f)(x) = E[f(N x) | x] and S (f) = E[f(x) f(N x)] = E[f T f]. • T has the eigenvectors u. S(x) = i 2 S xi, corresponding to the eigenvalues |S|. • Proof: Txi = E[N xi | xi] = (1 - ) xi - xi = xi • {Us} is an orthogonal basis. • f(x) = S fs u. S(x) : = Fourier expansion of f. • fs = E[f*u. S] : = Fourier coefficient at S. • E[f*g] = S fs gs ) S f. S 2 = 1 • Conclusion: S (f) = S f. S 2 |S|. • Thm (Kalai): PDX(f) = ¼ - ¾ S 1/3(f) 1/6/2022 U 1, 2, 3 U 1 17

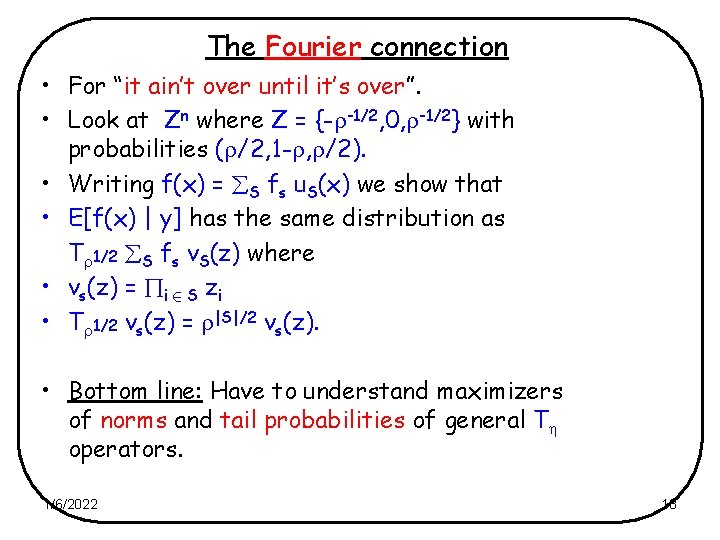
The Fourier connection • For “it ain’t over until it’s over”. • Look at Zn where Z = {- -1/2, 0, -1/2} with probabilities ( /2, 1 - , /2). • Writing f(x) = S fs u. S(x) we show that • E[f(x) | y] has the same distribution as T 1/2 S fs v. S(z) where • vs(z) = i 2 S zi • T 1/2 vs(z) = |S|/2 vs(z). • Bottom line: Have to understand maximizers of norms and tail probabilities of general T operators. 1/6/2022 18

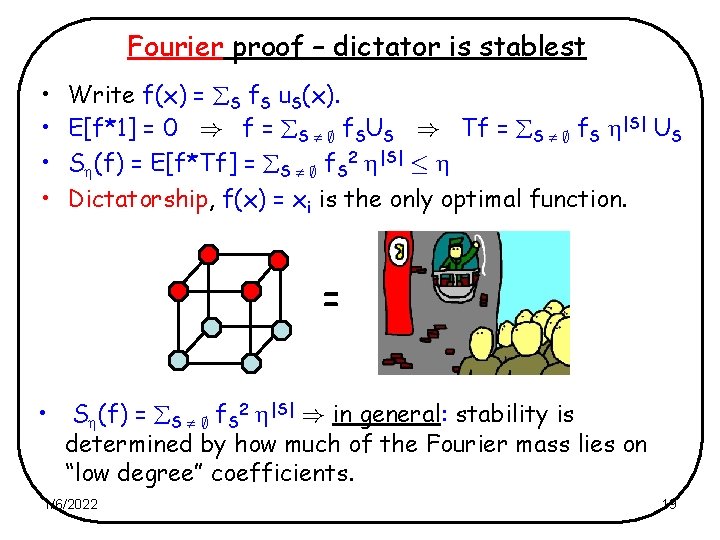
Fourier proof – dictator is stablest • • Write f(x) = S f. S u. S(x). E[f*1] = 0 ) f = S ; f. SUS ) Tf = S ; f. S |S| US S (f) = E[f*Tf] = S ; f. S 2 |S| · Dictatorship, f(x) = xi is the only optimal function. = • S (f) = S ; f. S 2 |S| ) in general: stability is determined by how much of the Fourier mass lies on “low degree” coefficients. 1/6/2022 19

Reminder: Majority is Stablest • From now on we will try to prove it … 1/6/2022 20

From discrete to Gaussian stability • Consider the Gaussian measure on Rk. • Suppose f : Rk ! [-1, 1] is “smooth” and EG[f] = 0. • Let fn : {-1, 1}kn ! [-1, 1] be defined by fn(x) = f((x 1+…+xn)/n 1/2, …, (x(k-1)n+1+…+xkn)/n 1/2) • By smoothness: limn ! 1 max 1 · i · kn Ii(fn) = 0. • By the Central Limit Theorem: limn ! 1 EU[fn(x)] = 0 & • limn ! 1 EU[fn*T fn] = EG[f(X) f(Y)], where • X Gaussian vector and Y = U X. • U X = X + (1 - 2)1/2 Z, where Z independent Gaussian. • (X, Y) = (X 1, …, XK, Y 1, …, Yk) is a normal vector with • E[Xi Xj] = E[Yi Yj] = i, j and E[Xi Yj] = i, j 1/6/2022 21

From discrete to Gaussian stability 2 • “Majority is Stablest” ) • for all smooth f: Rk ! [-1, 1] with EG[f] = 0: EG[f U f] = EG[f(X) f(Y)] · 1 – (2/ ) arcos • By “density” the same should hold for all f 2 L 2. • Note that we obtain equality when m(x) = sgn(x 1) – m(x) is the “limit” of the majority functions. • So “Majority is Stablest” implies Gaussian results that may be easier to verify. • Indeed was proved by Borell 85 using Erhard symmetrization. • Easiest to see via 2 pt symmetrization on the sphere. 1/6/2022 22

From Gaussian to discrete stability • Is there a way to deduce the discrete results from the Gaussian result? • Let’s look at the CLT theorem again: • CLT: If |a|2 = 1 and supi |ai| · then • ai xi ~ N where ~ means – supx |P[ i ai xi · x] – P[N · x]| · and ! 0 as ! 0 • Different formulation: • Let f : {-1, 1}n ! R be a linear function: f(x) = ai xi and – |f|2 = 1. – Ii(f) · for all i. • Then f ~ ai Ni where • Ni are i. i. d. Gaussians. 1/6/2022 23
![From Gaussian to discrete stability A new limit theorem MODonnellOleszkiewicz Let f From Gaussian to discrete stability • A new limit theorem [M+O’Donnell+Oleszkiewicz]: • Let f](https://slidetodoc.com/presentation_image_h2/584edb5196ef674e2cf54991b7badca9/image-24.jpg)
From Gaussian to discrete stability • A new limit theorem [M+O’Donnell+Oleszkiewicz]: • Let f = 0 < |S| · k a. S i 2 S xi be a degree k polynomial such that – |f|2 = 1 – Ii(f) · for all i. • Then f ~ 0 < |S| · k a. S i 2 S Ni • Similar result for other discrete spaces. • Generalizes: – CLT – Gaussian chaos results for U and V statistics. 1/6/2022 24

A proof sketch : maj is stablest • Idea: Truncate and follow your nose. • Suppose f : {-1, 1}n ! [-1, 1] has small influences but E[f T f] = is large. • Then the same is true for g = T f ( ( ) < 1). • Let h = |S| · k g. S u. S then |h-g|2 is small. • Let h’ = |S| · k g. S i 2 S Ni • Then: <h, T h> = <h’, U h’> is large and by the new limit theorem: • h’ is close in L 2 to a [-1, 1] R. V. • Take g’(x) = h’(x) if |h’(x)| · 1 and g’(x) = sgn(h’(x)). • E[g’ U g’] is too large – contradiction! + 1/6/2022 25

A proof sketch : new limit theorem • • Recall: p a degree k multi-linear polynomial with: |p|2 = 1 and Ii(p) · for all i. Want to show p(x 1, …, xn) ~ p(N 1, …, Nn). Step 1 (classical): Suffices to show that for every smooth F --|F’’’| · C, it holds that • E[F(p(x 1, …, xn)] is close to E[F(p(N 1, …, Nn))]. 1/6/2022 26

Sketch of proof of Lemma • p(…, xi-1, Ni, …) = Ri + Ni Si and p(…, xi, Ni+1, …) = Ri + xi Si • By Calculus and independence: • |E[F(Ri + Ni Si)] – E[F(Ri + xi Si)] |· sup |F’’’| (E[|xi|3] + E[|Ni|3]) E[|Si|3] /6 · C E[|Si|3] • If we could say E[|Si|3] · C’ E[Si 2]3/2 then we’re done since E[Si 2]3/2 = Ii 3/2. • This is a “hyper-contractive” inequality. • So all that is left is to prove: 1/6/2022 27

Sketch of proof of Lemma • This is a standard argument. • Somewhat similar results (same proof idea) – Rotar (75) Slightly different setting. No Berry-Essen bounds. Lindenberg conditions instead of hypercontractivity. – Chaterjee (04) Elegant but conditions are too strong – uses worst case influences instead of average case. 1/6/2022 28

Conclusion • We’ve seen how Gaussian techniques can help solve discrete stability problems. • Future work: • Better understanding of the dependency on all parameters for general prob. spaces. • Applications to – Social choice. – PCP’s – Learning. • Sometimes need better Gaussian understanding. • Example: – Suppose we want to partition Gaussian space to 3 parts of equal measure – what is the most stable way? 1/6/2022 29

1/6/2022 30

Properties of voting schemes • Some properties of voting schemes: • Some properties we may require from voting schemes: The function f is anti-symmetric: f(~x) = ~f(x) where ~(z 1, …, zn) = (1 – z 1, …, 1 -zn). • The function f is balanced: EUnif[f] = 0. • stronger support in a candidate shouldn’t hurt her: The function f is monotone: x ¸ y ) f(x) ¸ f(y), where x ¸ y if xi ¸ yi for all i. • Note that both majority and the electoral college are anti-symmetric and monotone. 1/6/2022 31

Stability of voting schemes • Which voting schemes are more robust against noise? • Simplest model of noise: The voting machine flips each vote independently with probability (not realistic). • Simplest model of voter distribution: i. i. d. distribution where each voter votes 0/1 with probability ½. • Very far from reality … • Buy maybe good model for “critical voting”. 1/6/2022 32
 Mossel bay municipality bylaws
Mossel bay municipality bylaws Nelson mandela bay municipality building regulations
Nelson mandela bay municipality building regulations Bim curriculum
Bim curriculum Life bay view
Life bay view Quarks chaos and christianity
Quarks chaos and christianity Chaos theory and cryptology
Chaos theory and cryptology Fractals and chaos
Fractals and chaos Simplex method sensitivity analysis
Simplex method sensitivity analysis Selectivity of radio receiver
Selectivity of radio receiver Sensitivity analysis and duality
Sensitivity analysis and duality Sensitivity analysis and interpretation of solution
Sensitivity analysis and interpretation of solution Na początku był chaos biblia
Na początku był chaos biblia Gustatorischer cortex
Gustatorischer cortex Chaos monsters bible
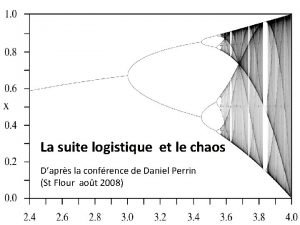
Chaos monsters bible Suite logistique
Suite logistique Stamboom poseidon
Stamboom poseidon Tartarus family tree
Tartarus family tree Chinese symbol for chaos
Chinese symbol for chaos Copyright chaos
Copyright chaos Third iteration jurassic park
Third iteration jurassic park Chaos sound test
Chaos sound test Chaos theory management
Chaos theory management Six degrees of separation kandinsky
Six degrees of separation kandinsky Nihilists
Nihilists Iq test
Iq test Chaos mitologia drzewo genealogiczne
Chaos mitologia drzewo genealogiczne Chaos in greek mythology
Chaos in greek mythology Drupal chaos tools
Drupal chaos tools Chaos in de klas
Chaos in de klas Aip chaos
Aip chaos Antipathy synonym
Antipathy synonym Describe athena
Describe athena Gaia greek mythology family tree
Gaia greek mythology family tree