Ratios and Proportions Outline Ratios What is a







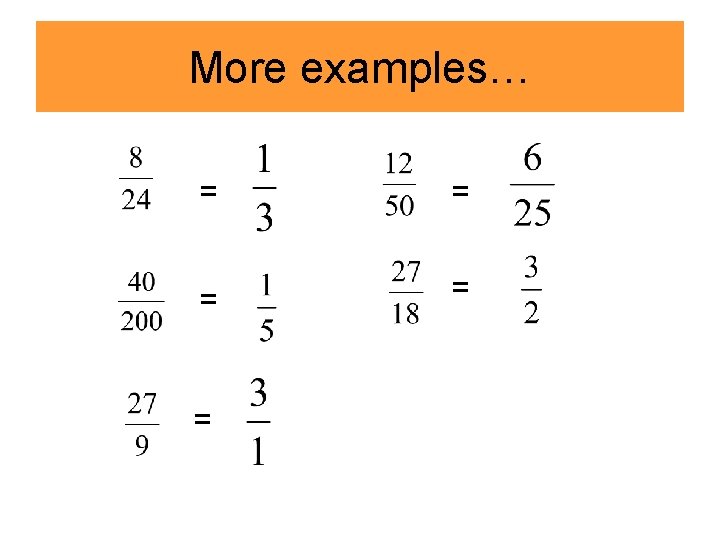










- Slides: 23

Ratios and Proportions

Outline: • Ratios! What is a Ratio? How to Use Ratios? How to Simplify? Proportions! What is a proportion? Properties of proportions? How to use proportions? • Mysterious Problems…

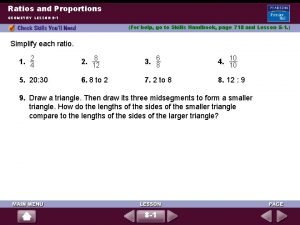
What is a Ratio? • A ratio is a comparison of two numbers. • Ratios can be written in three different ways: a to b a: b Because a ratio is a fraction, b can not be zero Ratios are expressed in simplest form

How to Use Ratios? • The ratio of boys and girls in the class is 12 to 11. This means, for every 12 boys you can find 11 girls to match. How could manybe dogs cats do • There justand 12 boys, 11 I have? We don’t know, all we girls. knowcould is if they’d fight, • There be 24 start boys, a 22 girls. eachcould dog has to fight 2 cats. • There be 120 boys, 110 4 cm girls…a huge class 1 cm • The ratio of length and width of this rectangle is 4 to 1. What is the ratio if the rectangle is 8 cm long and 2 cm wide? Still 4 to 1, because for every 4 cm, you can find 1 cm to match . • The ratio of cats and dogs at my home is 2 to 1

How to simplify ratios? • The ratios we saw on last slide were all simplified. How was it done? Ratios can be expressed The ratio of boys and girls in the class is The ratio of the rectangle is in fraction form… This allows us to do math on them. The ratio of cats and dogs in my house is

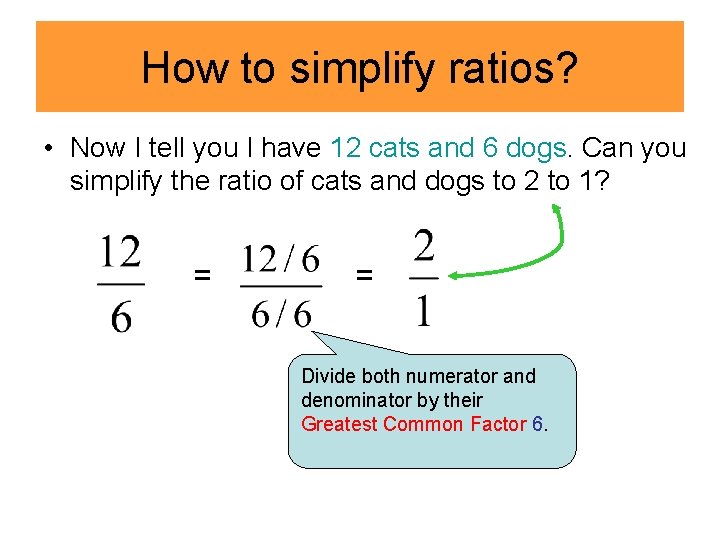
How to simplify ratios? • Now I tell you I have 12 cats and 6 dogs. Can you simplify the ratio of cats and dogs to 2 to 1? = = Divide both numerator and denominator by their Greatest Common Factor 6.

How to simplify ratios? A person’s arm is 80 cm, he is 2 m tall. Find the ratio of the length of his arm to his total height To compare them, we need to convert both numbers into the same unit …either cm or m. • Let’s try cm first! Once we have the same units, we can simplify them.

How to simplify ratios? • Let’s try m now! Once we have the same units, they simplify to 1. To make both numbers integers, we multiplied both numerator and denominator by 10

How to simplify ratios? • If the numerator and denominator do not have the same units it may be easier to convert to the smaller unit so we don’t have to work with decimals… 3 cm/12 m = 3 cm/1200 cm = 1/400 2 kg/15 g = 2000 g/15 g = 400/3 5 ft/70 in = (5*12)in / 70 in = 60 in/70 in = 6/7 2 g/8 g = 1/4 Of course, if they are already in the same units, we don’t have to worry about converting. Good deal
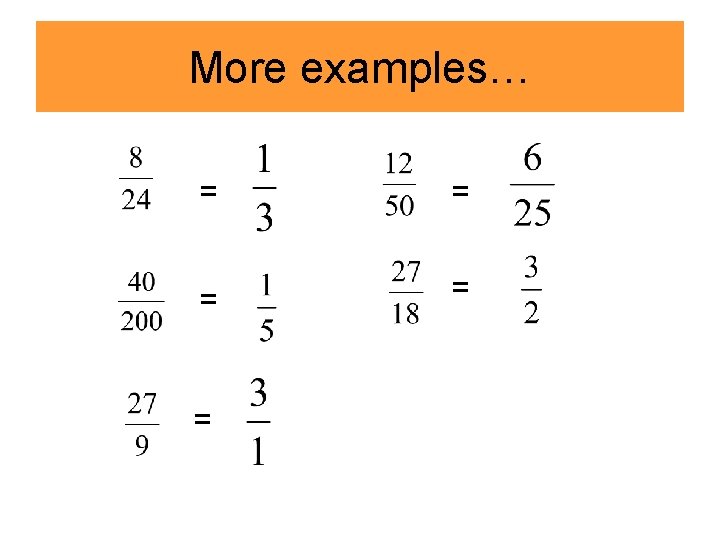
More examples… = = =

Now, on to proportions! What is a proportion? A proportion is an equation that equates two ratios The ratio of dogs and cats was 3/2 The ratio of dogs and cats now is 6/4=3/2 So we have a proportion :

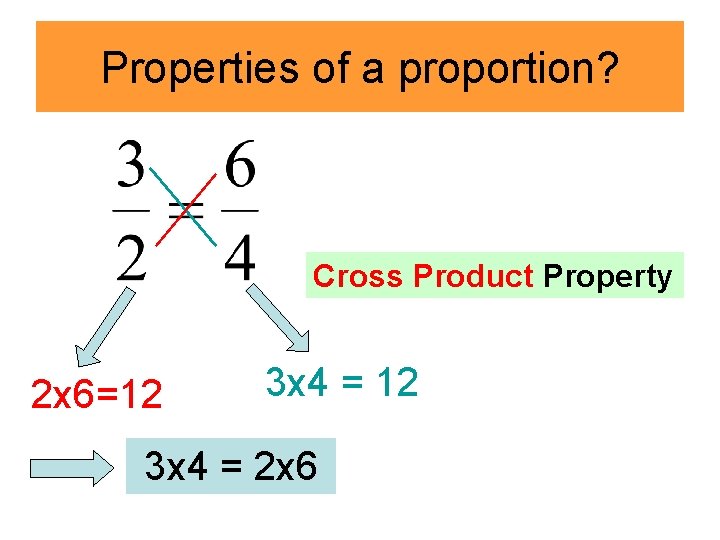
Properties of a proportion? Cross Product Property 2 x 6=12 3 x 4 = 2 x 6

Properties of a proportion? • Cross Product Property ad = bc means extremes

Properties of a proportion? Let’s make sense of the Cross Product Property… For any numbers a, b, c, d:

Properties of a proportion? • Reciprocal Property If Then Can you see it? If yes, can you think of why it works?

How about an example? Solve for x: 7(6) = 2 x 42 = 2 x 21 = x Cross Product Property

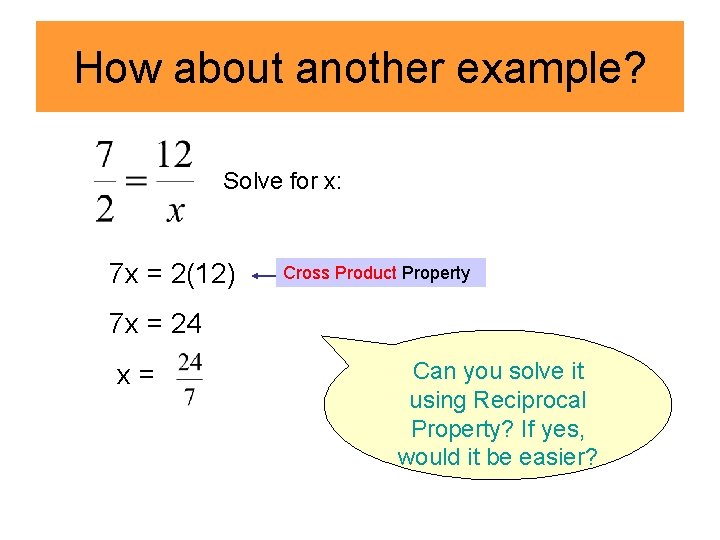
How about another example? Solve for x: 7 x = 2(12) Cross Product Property 7 x = 24 x= Can you solve it using Reciprocal Property? If yes, would it be easier?

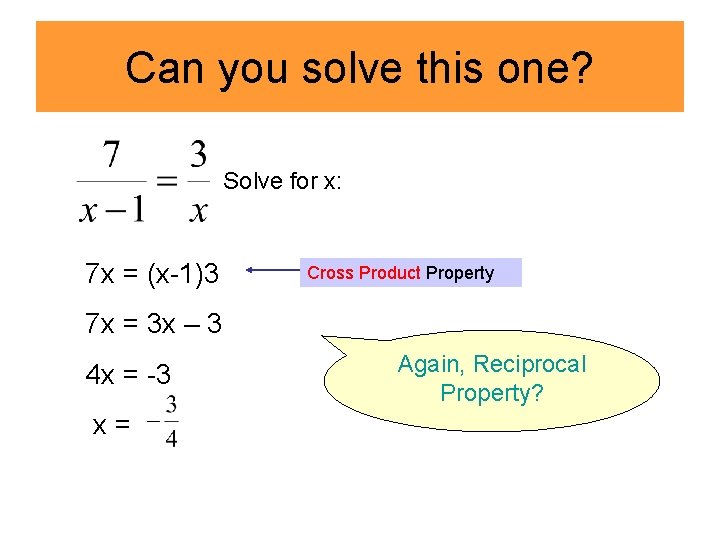
Can you solve this one? Solve for x: 7 x = (x-1)3 Cross Product Property 7 x = 3 x – 3 4 x = -3 x= Again, Reciprocal Property?

Now you know enough about properties, let’s solve the Mysterious problems! If your car gets 30 miles/gallon, how many gallons of gas do you need to commute to school everyday? 5 miles to home 5 miles to school Let x be the number gallons we need for a day: x= Gal Can you solve it from here?

5 miles to home 5 miles to school So you use up 1/3 gallon a day. How many gallons would you use for a week? Let t be the number of gallons we need for a week: What property is this? Gal

So you use up 5/3 gallons a week (which is about 1. 67 gallons). Consider if the price of gas is 3. 69 dollars/gal, how much would it cost for a week? Let s be the sum of cost for a week: 3. 69(1. 67) = 1 s s = 6. 16 dollars 5 miles to home 5 miles to school

So what do you think? 5 miles 10 miles You pay about 6 bucks a week just to get to school! What about weekends? If you travel twice as much on weekends, say drive 10 miles to the Mall and 10 miles back, how many gallons do you need now? How much would it cost totally? How much would it cost for a month? Think proportionally!. . . It’s all about proportions!

 If abcd is a rectangle and m adb=55 what is the value of x
If abcd is a rectangle and m adb=55 what is the value of x Is a ratio a rate
Is a ratio a rate Proportion examples
Proportion examples 7-1 ratios & proportions
7-1 ratios & proportions Lesson quiz 4-2
Lesson quiz 4-2 Ratios and proportions review
Ratios and proportions review Proportion jeopardy
Proportion jeopardy Rates ratios and proportions worksheets
Rates ratios and proportions worksheets Geometry ratios and proportions
Geometry ratios and proportions Properties of proportion
Properties of proportion Algebra 1 proportions
Algebra 1 proportions Quiz 1: ratios, properties, and proportions
Quiz 1: ratios, properties, and proportions Notes on ratios
Notes on ratios Ratios and proportions guided notes
Ratios and proportions guided notes 2 6 rates ratios, and proportions answers
2 6 rates ratios, and proportions answers 1-8 rates ratios and proportions
1-8 rates ratios and proportions Quiz 1 ratios properties and proportions
Quiz 1 ratios properties and proportions Example of a sentence outline
Example of a sentence outline What are the ingredients and proportions in 3-2-1 dough
What are the ingredients and proportions in 3-2-1 dough Core focus on proportions and probability answer key
Core focus on proportions and probability answer key Definite composition example
Definite composition example Laws of definite and multiple proportions
Laws of definite and multiple proportions Means and extremes of proportions
Means and extremes of proportions Means and extremes examples
Means and extremes examples