Ratios Proportions and the Geometric Mean Ratios A












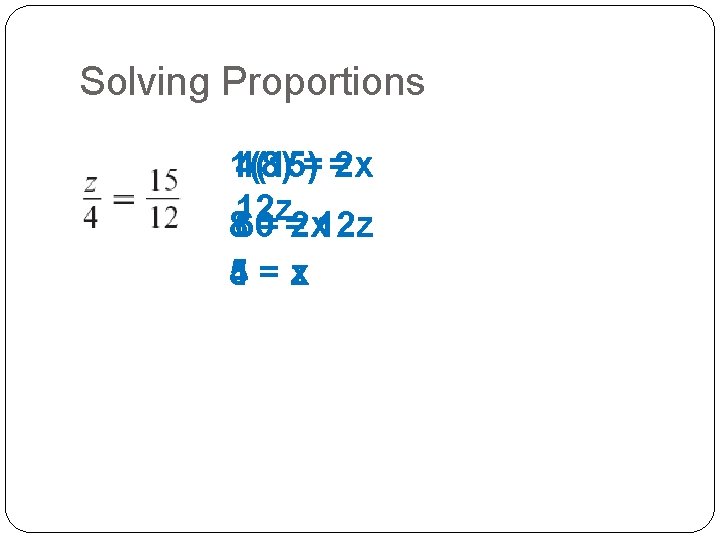
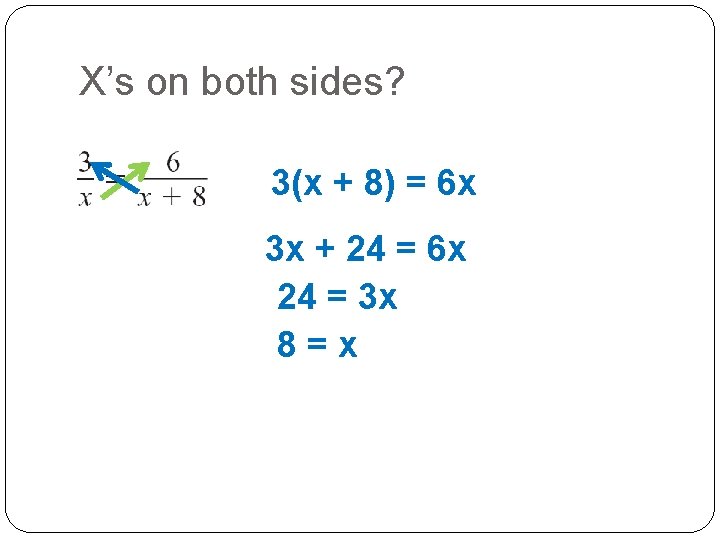
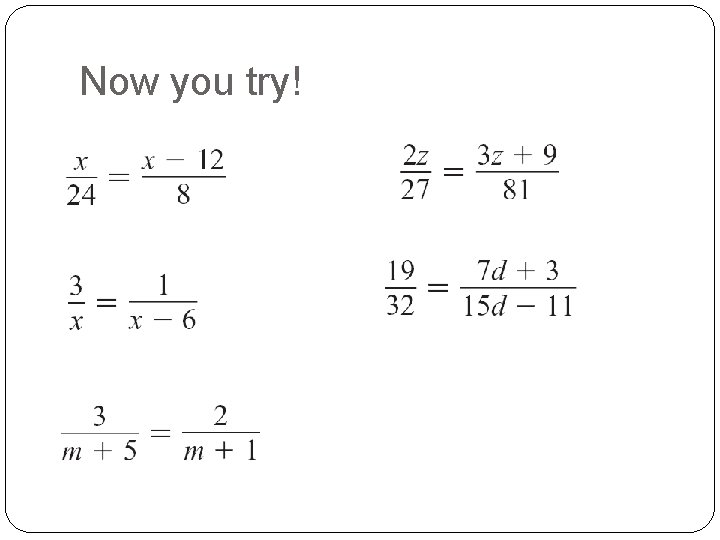




- Slides: 20

Ratios, Proportions, and the Geometric Mean

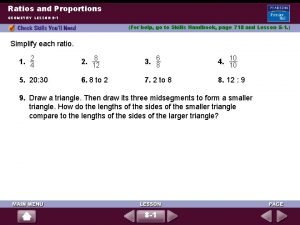
Ratios A ratio is a comparison of two numbers expressed by a fraction. The ratio of a to b can be written 3 ways: a: b a to b

Equivalent Ratios Equivalent ratios are ratios that have the same value. Examples: 1: 2 and 3: 6 5: 15 and 1: 3 6: 36 and 1: 6 2: 18 and 1: 9 4: 16 and 1: 4 7: 35 and 1: 5 Can you come up with your own?

Simplify the ratios to determine an equivalent ratio. 3 ft = 1 yard Convert 3 yd to ft 1 km = 1000 m Convert 5 km to m

Simplify the ratio Convert 2 ft to in

Use the number line to find the ratio of the distances

Using an Extended Ratio An extended ratio compares three (or more) numbers. In the extended ratio a : b : c, the ratios a : b, b : c, and a : c are all equivalent.

The lengths of the sides of a triangle are in the extended ratio 4 : 7 : 9. The perimeter is 60 cm. What are the lengths of the sides?

Triangles and ratios: finding interior angles The ratio of the 3 angles in a triangle are represented by 1: 2: 3. The 1 st angle is a multiple of 1, the 2 nd a multiple of 2 and the 3 rd a multiple of 3. =30 Angle 2 = 2 x =2(30) = 60 Angle 3 = 3 x = 3(30) = 90 Angle 1 = 1 x What do we know about the sum of the interior angles? 1 x + 2 x + 3 x = 180 6 x = 180 X = 30

Triangles and ratios: finding interior angles The ratio of the angles in a triangle are represented by 1: 1: 2. Angle 1 = 1 x = 1(45) = 45 Angle 1 = 1 x Angle 2 = 1 x = 1(45) = 45 Angle 2 = 1 x Angle 3 = 2 x = 2(45) = 90 Angle 3 = 2 x 1 x + 2 x = 180 4 x = 180 x = 45

Proportions, extremes, means Proportion: a mathematical statement that states that 2 ratios are equal to each other. mea ns extremes

Solving Proportions When you have 2 proportions or fractions that are set equal to each other, you can use cross multiplication. 1 y = 3(3) y = 9
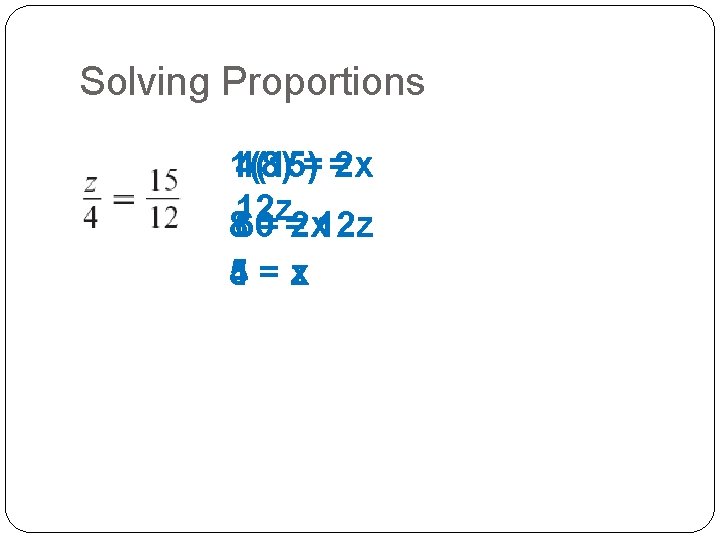
Solving Proportions 1(8) 4(15)= =2 x 12 z 860= =2 x 12 z 4 = zx 5

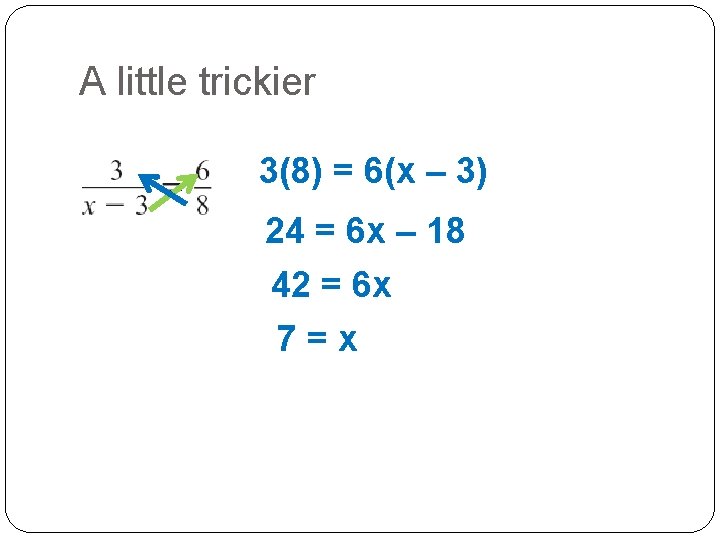
A little trickier 3(8) = 6(x – 3) 24 = 6 x – 18 42 = 6 x 7=x
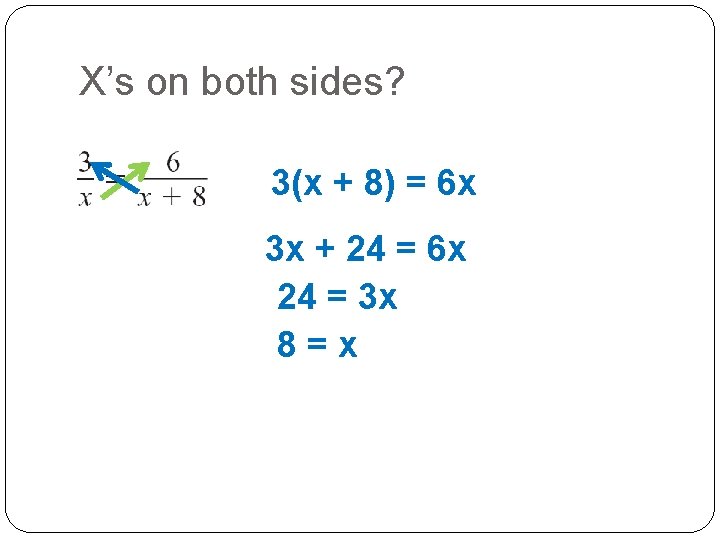
X’s on both sides? 3(x + 8) = 6 x 3 x + 24 = 6 x 24 = 3 x 8=x
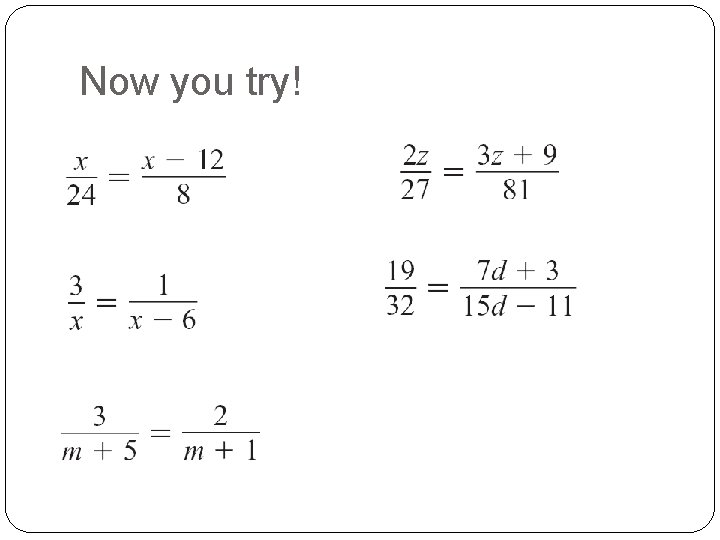
Now you try!

Now you try! x= 18 x=9 m=7 z=3 d=5

Geometric Mean When given 2 positive numbers, a and b the geometric mean satisfies:

Find the geometric mean x=2 x=3

Find the geometric mean x=9
 Practice 8-1 ratios and proportions answers
Practice 8-1 ratios and proportions answers Is a ratio a rate
Is a ratio a rate 7-1 ratios and proportions
7-1 ratios and proportions 7-1 ratios and proportions
7-1 ratios and proportions 4-1 lesson quiz
4-1 lesson quiz Ratios and proportions review
Ratios and proportions review Jeopardy ratios
Jeopardy ratios Rates ratios and proportions
Rates ratios and proportions Similarity ratio
Similarity ratio Ratios and proportions 7-1
Ratios and proportions 7-1 2-6 ratios and proportions answer key
2-6 ratios and proportions answer key Example of a proportion
Example of a proportion Notes on proportions
Notes on proportions Ratios and proportions guided notes
Ratios and proportions guided notes 2-6 ratios and proportions
2-6 ratios and proportions 1-8 rates ratios and proportions
1-8 rates ratios and proportions Quiz 1: ratios, properties, and proportions
Quiz 1: ratios, properties, and proportions Geometry bootcamp answers
Geometry bootcamp answers 8-1 geometric mean
8-1 geometric mean Geometric mean sas
Geometric mean sas Unit 1 lesson 3
Unit 1 lesson 3