Quantum Chemistry Lecture No 4 Schrdinger wave equation







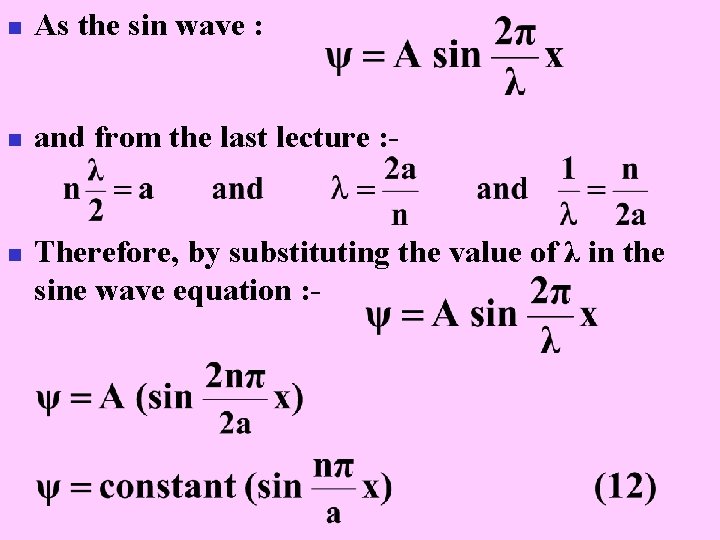


- Slides: 13

Quantum Chemistry Lecture No. 4 Schrödinger wave equation in one dimension Prof. Dr. Samih A. Halawy

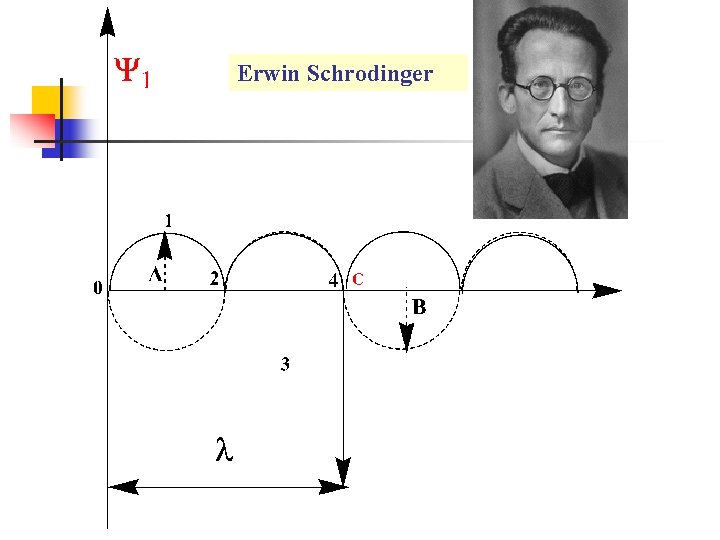
Quantum Chemistry -L 4 Schrödinger wave equation in one dimension : Consider a beam of particles on-a-line segment. These particles have a wave property. Using the (sin wave) to describe the wave movement and the wave function is ( ). The highest point of the wave A, is the amplitude of the wave at various (x) values. n

Erwin Schrodinger

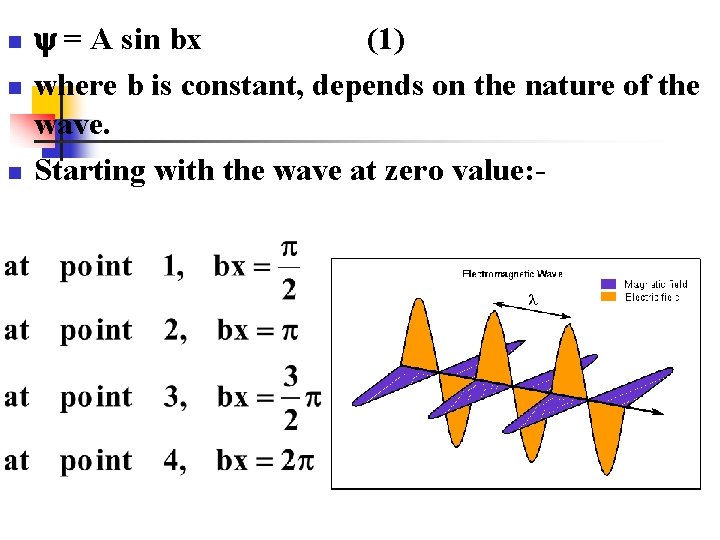
n n n = A sin bx (1) where b is constant, depends on the nature of the wave. Starting with the wave at zero value: -

n n n from zero to point C (4), that gives one wave length = λ, the wave length = x. Equation (1) can be rewritten as : By the same way we can describe the wave function of these particles by (cosine wave): -

n n n Combine the two equations together (2+3) for a complete description of the wave: - Taking the second derivative of the last equation (4), relative to x : - Substituting the value of ( ) from equation (4): -

n n n The wave length (λ) is calculated by : - where, h is Planck's constant and P is the linear momentum. substituting the value of 1/λ 2 in equation (6) : -

n The energy is more important than the momentum. Therefore, we well replace the energy by the linear momentum: ETotal = EKinetic + U(x) n Equation (8) can written as follows: - n

n Substituting the value of P 2 in equation (7) : - n multiplying with : n n The wave function describes the atomic and the molecular orbitals. E , the energy of electrons.

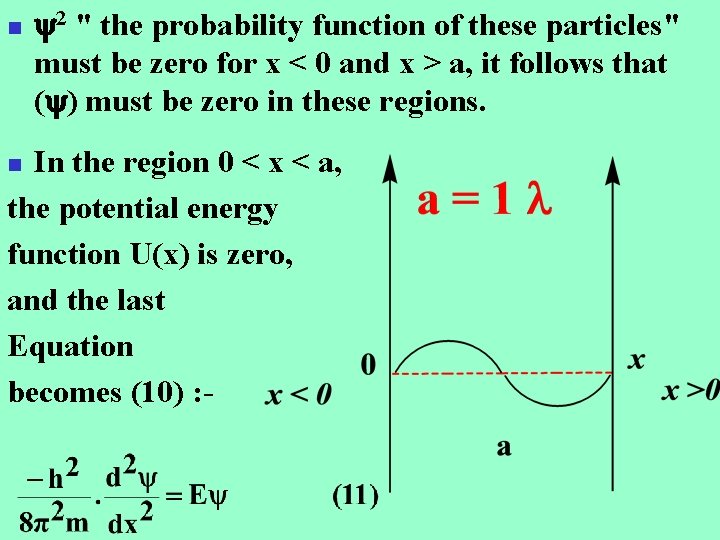
n 2 " the probability function of these particles" must be zero for x < 0 and x > a, it follows that ( ) must be zero in these regions. In the region 0 < x < a, the potential energy function U(x) is zero, and the last Equation becomes (10) : n
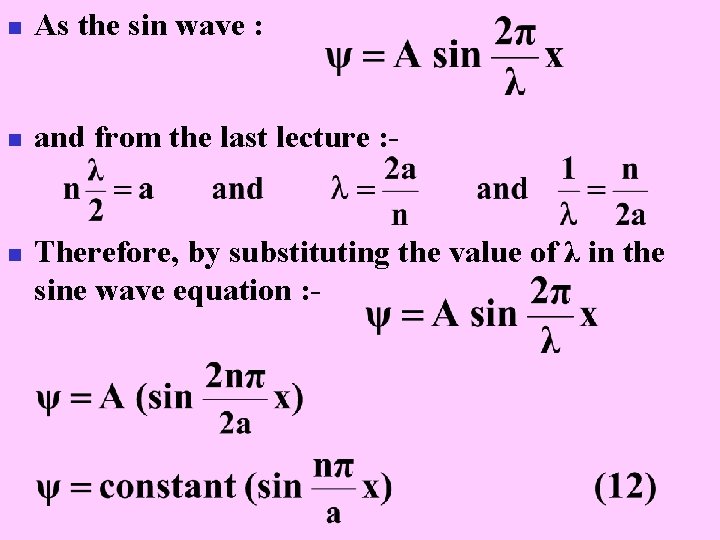
n As the sin wave : n and from the last lecture : - n Therefore, by substituting the value of λ in the sine wave equation : -

n n Functions that solve the differential equation and also satisfy the boundary x = 0 and x = a. : (11) ﺑﺄﺨـﺬ ﺍﻟﻤﺸﺘﻘﺔ ﺍﻟﺘﻔﻀﺎﻟﻴﺔ ﺍﻟﺜﺎﻧﻴﺔ ﻟﻠﻤﻌﺎﺩﻟﺔ ﺭﻗﻢ n Taking the second derivative of the left side of equation (11): - and the right side of equation (11) : -

n by replacing the value of from equation (12). Making equation (13) equal to equation (14) : n E is the total energy of a particle on a line segment. n
 Expectation value of position
Expectation value of position Schrdinger
Schrdinger Ewrin schrodinger
Ewrin schrodinger Schrdinger
Schrdinger Schrodinger time dependent equation
Schrodinger time dependent equation Equação de onda de schrodinger
Equação de onda de schrodinger Classical mechanics
Classical mechanics Quantum physics vs quantum mechanics
Quantum physics vs quantum mechanics 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Quantum physics wave function
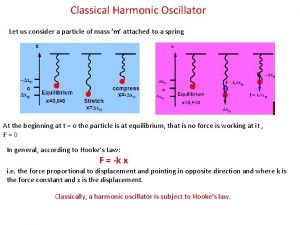
Quantum physics wave function Classical harmonic oscillator
Classical harmonic oscillator Wave function of quantum harmonic oscillator
Wave function of quantum harmonic oscillator Quantum physics wave function
Quantum physics wave function Review of quantum mechanics
Review of quantum mechanics