The Wave Equation The Wave equation describes sound

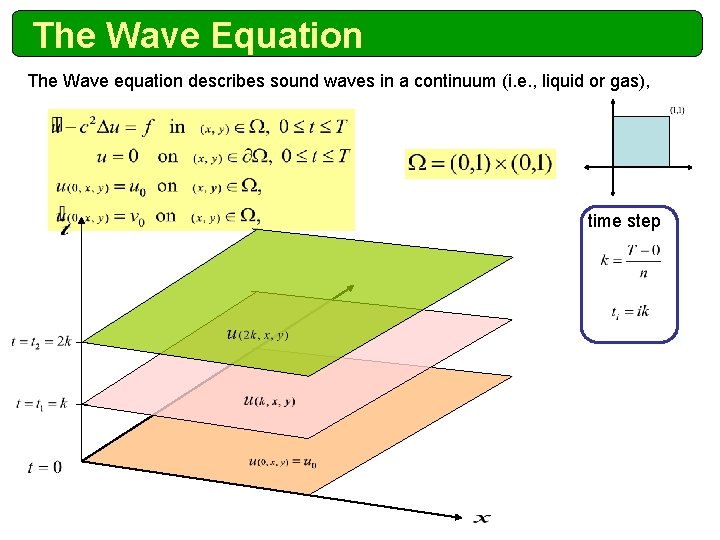
The Wave Equation The Wave equation describes sound waves in a continuum (i. e. , liquid or gas), time step

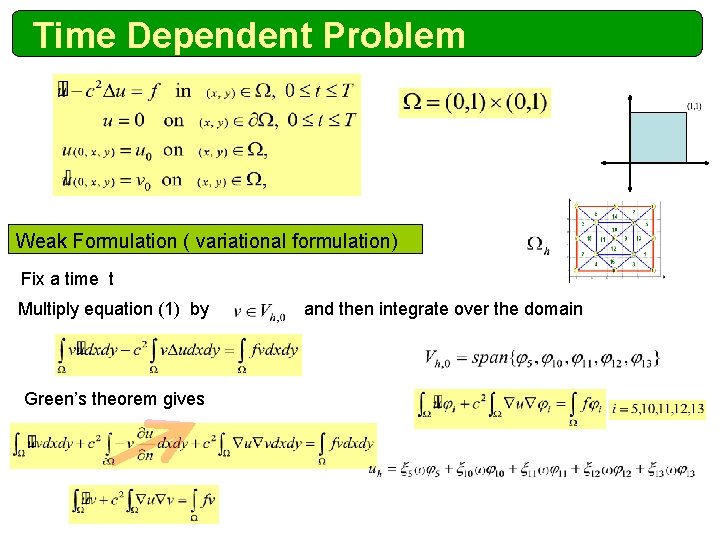
Time Dependent Problem Weak Formulation ( variational formulation) Fix a time t Multiply equation (1) by Green’s theorem gives and then integrate over the domain

Variational Formulation Spatial Discretization

Spatial Discretization spatial semi-discretization equation Reduce into first order

Spatial Discretization spatial semi-discretization equation Reduce into first order

Spatial Discretization spatial semi-discretization equation Crank-Nicolson Method

Fully Discrete Equation Crank-Nicolson Method (Matrix Form)

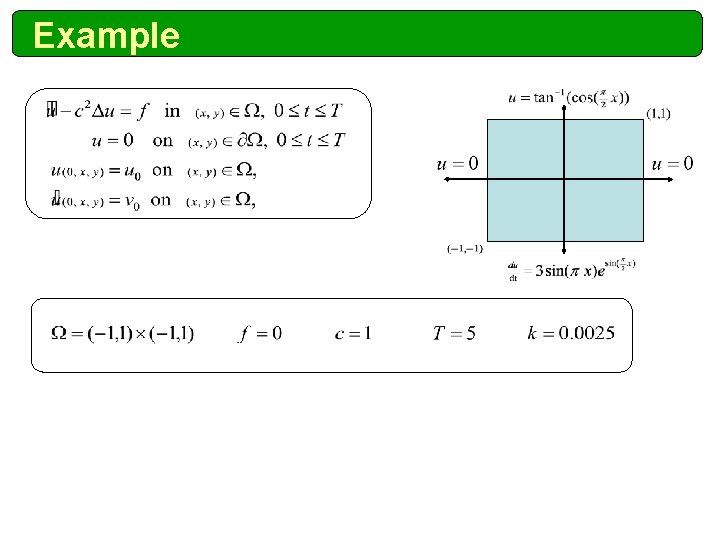
Example

Computer Implementation % % We solve the wave equation d 2 u/dt 2 -div(grad(u))=0 on a square. % To speed up plot, we interpolate to a rect grid. % Problem definition g='squareg'; % The unit square b='squareb 3'; % 0 on the left and right boundaries and % 0 normal derivative on the top & bottom. c=1; a=0; f=0; d=1; % pde coeff % Mesh [p, e, t]=initmesh('squareg'); % The initial conditions: % u(0)=atan(cos(pi/2*x)) and % dudt(0)=3*sin(pi*x). *exp(sin(pi/2*y)) x=p(1, : )'; y=p(2, : )'; u 0=atan(cos(pi/2*x)); ut 0=3*sin(pi*x). *exp(sin(pi/2*y)); % We want the sol at 31 pts in time between 0 and 5. n=401; tlist=linspace(0, 5, n); % Solve hyperbolic problem uu=hyperbolic(u 0, ut 0, tlist, b, p, e, t, c, a, f, d); delta=-1: 0. 1: 1; [uxy, tn, a 2, a 3]=tri 2 grid(p, t, uu(: , 1), delta); gp=[tn; a 2; a 3]; % Make the animation newplot; M=moviein(n); umax=max(uu)); umin=min(uu)); for i=1: n, . . . pdeplot(p, e, t, 'xydata', uu(: , i), 'zdata', . . . uu(: , i), 'zstyle', 'continuous', . . . 'mesh', 'off', 'xygrid', 'on', . . . 'gridparam', gp, 'colorbar', 'off'); . . . axis([-1 1 umin umax]); caxis([umin umax]); M(: , i)=getframe; end

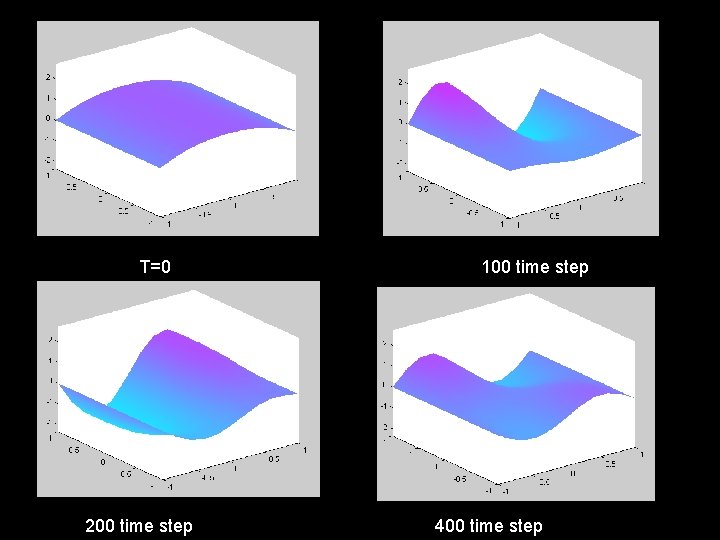
T=0 200 time step 100 time step 400 time step