Przetwarzanie i rozpoznawanie obrazw Filtracja obrazw 1 Definicje

Przetwarzanie i rozpoznawanie obrazów Filtracja obrazów 1

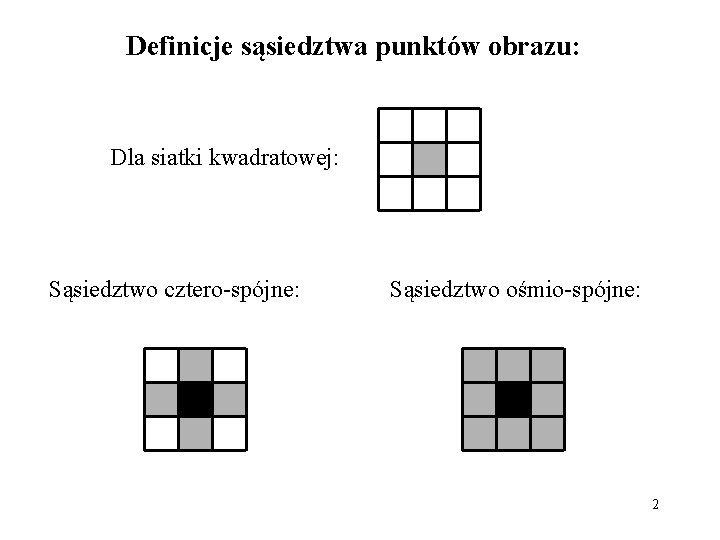
Definicje sąsiedztwa punktów obrazu: Dla siatki kwadratowej: Sąsiedztwo cztero-spójne: Sąsiedztwo ośmio-spójne: 2

Sąsiedztwo dalsze Najbliższe otoczenie [3 3] analizowanego punktu f(x, y): f(x-1, y-1) f(x+1, y-1) f(x-1, y) f(x+1, y) f(x-1, y+1) f(x+1, y+1) 3

Filtracja liniowa w dziedzinie przestrzennej: Dwuwymiarowa operacja splotu dla tzw. maski h oraz macierzy określającej obraz: 4

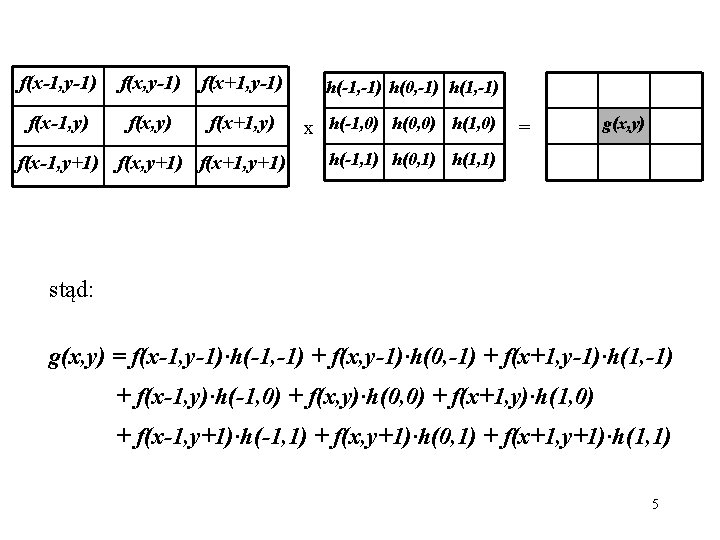
f(x-1, y-1) f(x+1, y-1) f(x-1, y) f(x+1, y) f(x-1, y+1) f(x+1, y+1) h(-1, -1) h(0, -1) h(1, -1) x h(-1, 0) h(0, 0) h(1, 0) = g(x, y) h(-1, 1) h(0, 1) h(1, 1) stąd: g(x, y) = f(x-1, y-1)·h(-1, -1) + f(x, y-1)·h(0, -1) + f(x+1, y-1)·h(1, -1) + f(x-1, y)·h(-1, 0) + f(x, y)·h(0, 0) + f(x+1, y)·h(1, 0) + f(x-1, y+1)·h(-1, 1) + f(x, y+1)·h(0, 1) + f(x+1, y+1)·h(1, 1) 5

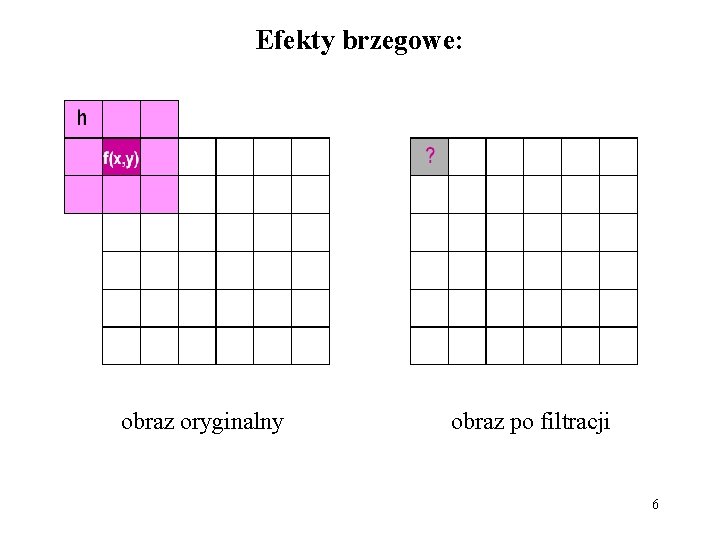
Efekty brzegowe: obraz oryginalny obraz po filtracji 6

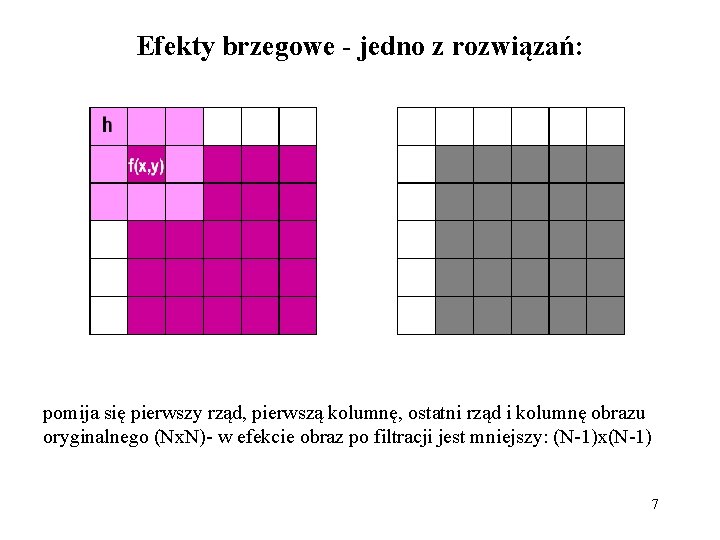
Efekty brzegowe - jedno z rozwiązań: pomija się pierwszy rząd, pierwszą kolumnę, ostatni rząd i kolumnę obrazu oryginalnego (Nx. N)- w efekcie obraz po filtracji jest mniejszy: (N-1)x(N-1) 7

Filtry dolnoprzepustowy: Tablica mnożników filtru: oryginał dolnoprzepustowy Aby zachować wartość średnią obrazu, suma elementów maski musi być równa 1. Wszystkie mnożniki muszą być wartościami dodatnimi. 8

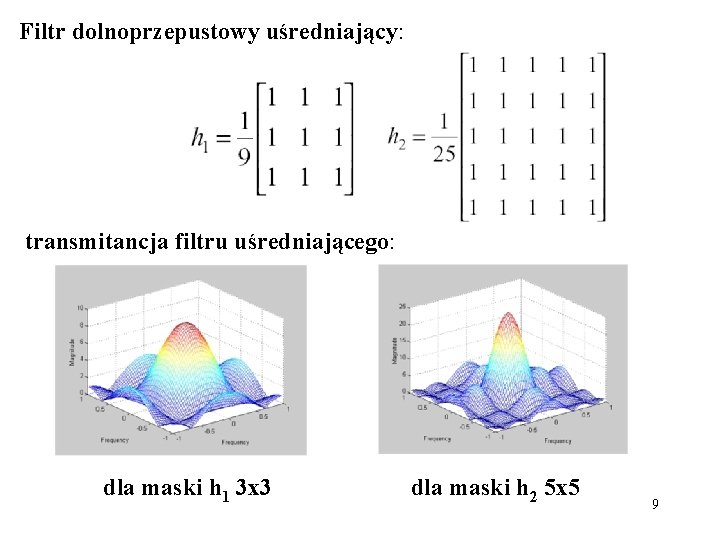
Filtr dolnoprzepustowy uśredniający: transmitancja filtru uśredniającego: dla maski h 1 3 x 3 dla maski h 2 5 x 5 9

Zastosowania filtru uśredniającego: oryginał 3 x 3 5 x 5 10

Zastosowania filtru dolnoprzepustowego cd: Obraz oryginalny: Wynik działania filtru dolnoprzepustowego: 11

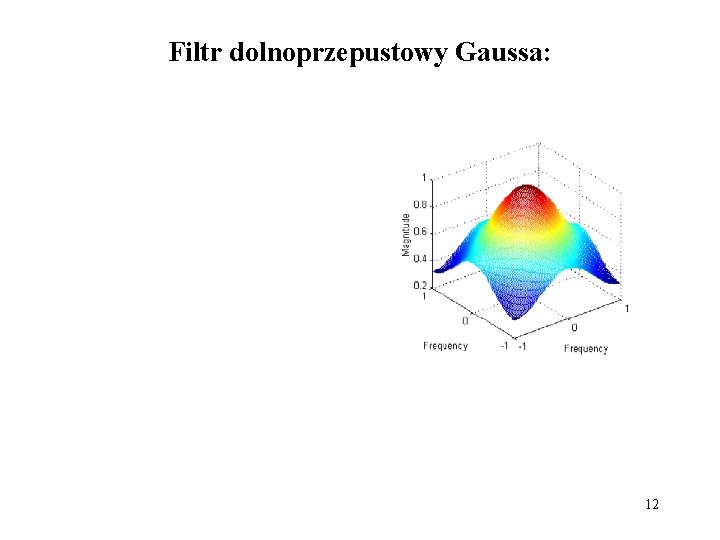
Filtr dolnoprzepustowy Gaussa: 12

Filtr dolnoprzepustowy Gaussa: oryginał po filtracji 13

Filtry górnoprzepustowy : Tablica mnożników filtru: oryginał górnoprzepustowy Aby wyeliminować składową stałą z obrazu, suma elementów maski musi być równa 0. Mnożniki mogą być dodatnie lub ujemne. 14

Zastosowania filtrów górnoprzepustowych: obraz rozmyty obraz po filtracji górnoprzepustowej, z zachowaniem wartości średniej 15

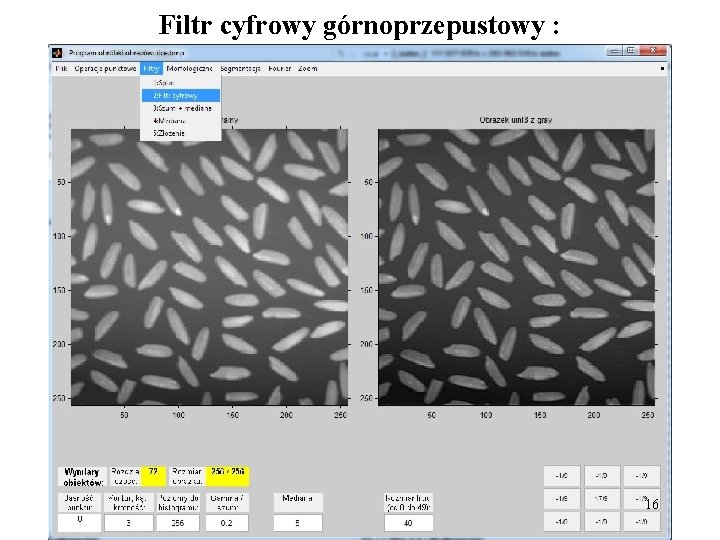
Filtr cyfrowy górnoprzepustowy : 16

Zapis programu: h(1, 1)=str 2 num(get(e 1, 'string')); % odczyt elementu maski filtru h(1, 2)=str 2 num(get(e 2, 'string')); h(1, 3)=str 2 num(get(e 3, 'string')); h(2, 1)=str 2 num(get(e 4, 'string')); h(2, 2)=str 2 num(get(e 5, 'string')); h(2, 3)=str 2 num(get(e 6, 'string')); h(3, 1)=str 2 num(get(e 7, 'string')); h(3, 2)=str 2 num(get(e 8, 'string')); h(3, 3)=str 2 num(get(e 9, 'string')); waga=sum(h)) im 2=filter 2(h, im); subplot('position', [0. 03 0. 22 0. 45 0. 73]), imshow(im), title('Obraz oryginalny') minimum 1=min(im 2)) maksimum 1=max(im 2)) 17

Zapis programu cd. : im 3=mat 2 gray(im 2); subplot('position', [0. 53 0. 22 0. 45 0. 73]), imshow(im 3), title('Obrazek intensywności') minimum 2=min(im 3)) maksimum 2=max(im 3)) im 4=uint 8(round(im 3*255)); minimum 3=min(im 4)) maksimum 3=max(im 4)) pause(1) subplot('position', [0. 53 0. 22 0. 45 0. 73]), imshow(im 4), title('Obrazek uint 8 z gray') 18

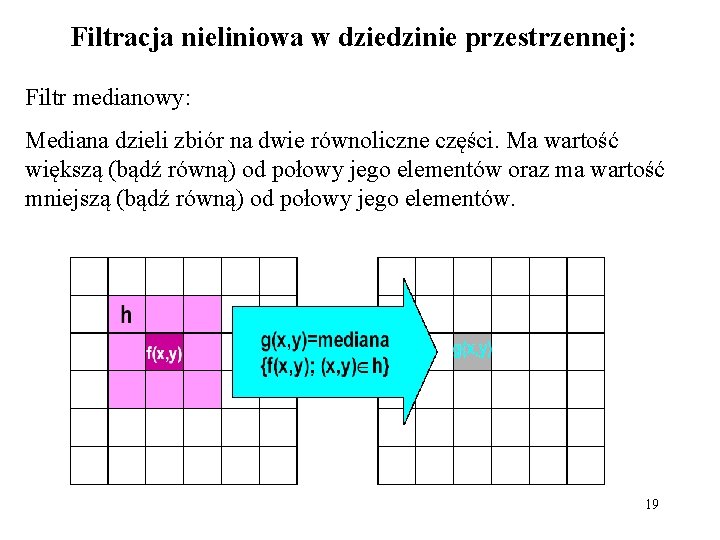
Filtracja nieliniowa w dziedzinie przestrzennej: Filtr medianowy: Mediana dzieli zbiór na dwie równoliczne części. Ma wartość większą (bądź równą) od połowy jego elementów oraz ma wartość mniejszą (bądź równą) od połowy jego elementów. 19

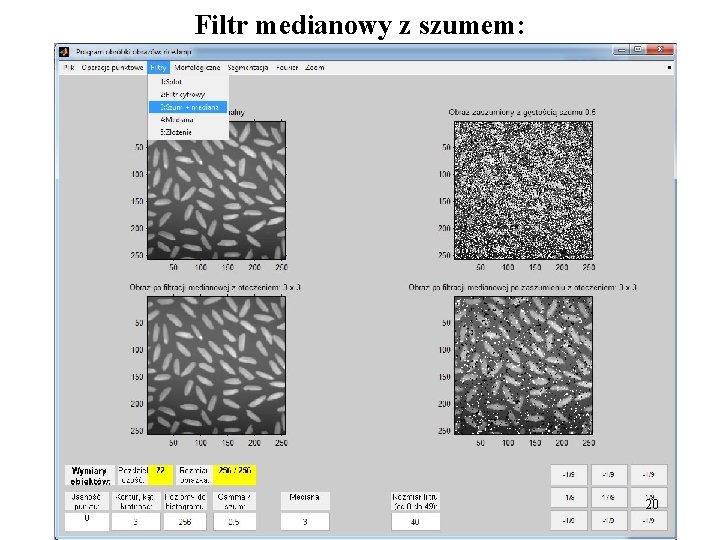
Filtr medianowy z szumem: 20

Filtr medianowy z szumem 0. 2 i medianą 3 x 3: 21

Filtr medianowy z szumem 0. 2 i medianą 5 x 5 : 22

Zapis programu: subplot('position', [0. 03 0. 6 0. 45 0. 3]), imshow(im), title('Obraz oryginalny') den=str 2 num(get(t 4, 'string')); im 2=imnoise(im, 'salt & pepper', den); subplot('position', [0. 53 0. 6 0. 45 0. 3]), imshow(im 2), title(['Obraz zaszumiony z gęstością szumu ', num 2 str(gam)]) poz=str 2 num(get(t 7, 'string')); im 3=medfilt 2(im, [poz, poz]); subplot('position', [0. 03 0. 22 0. 45 0. 3]), imshow(im 3), title(['Obraz po filtracji medianowej z otoczeniem: ', num 2 str(poz), ' x ', num 2 str(poz)]) im 4=medfilt 2(im 2, [poz, poz]); subplot('position', [0. 53 0. 22 0. 45 0. 3]), imshow(im 4), title(['Obraz po filtracji medianowej po zaszumieniu z otoczeniem: ', num 2 str(poz), ' x ', num 2 str(poz)]) 23

Porównanie filtrów medianowego i uśredniającego: 24

Porównanie efektów brzegowych filtr medianowy w: Corel’u: Matlab’ie: 25

Porównanie efektów brzegowych filtr medianowy w: Corel’u: Matlab’ie: 26

Detekcja brzegów: Brzegiem nazywamy granice pomiędzy dwoma obszarami o różnych jasnościach. Detekcja brzegów obszarów pozwala na identyfikację położenia obiektów w obrazie. Z tego też względu metody detekcji brzegów należą do najważniejszych narzędzi w przetwarzaniu i analizie obrazów. Większość metod detekcji brzegów bazuje na wyznaczaniu lokalnych pochodnych obrazu (tzw. operatorów gradientowych). 27

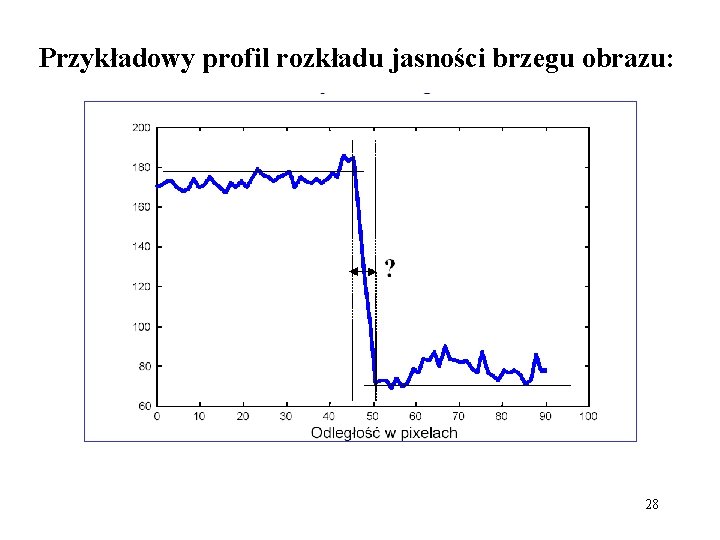
Przykładowy profil rozkładu jasności brzegu obrazu: 28

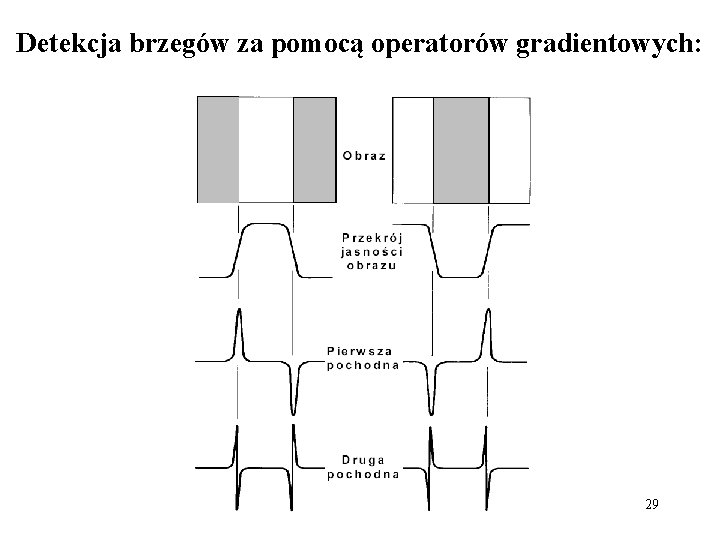
Detekcja brzegów za pomocą operatorów gradientowych: 29

Detektory linii - wyglądają tak, jak linia którą próbują znaleźć. Duża wartość w środku otoczona małymi wartościami. 30

Detektory linii: 31

Detektory linii: 32

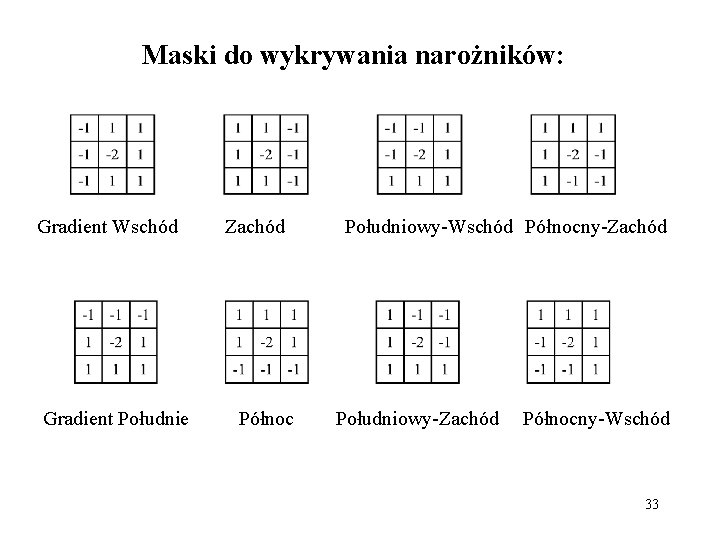
Maski do wykrywania narożników: Gradient Wschód Gradient Południe Zachód Północ Południowy-Wschód Północny-Zachód Południowy-Zachód Północny-Wschód 33

Maski do wykrywania narożników: 34

Podstawowe własności operatorów gradientowych: • pierwsza pochodna obrazu może być wykorzystana do detekcji brzegu oraz jego kierunku, • punkt zmiany znaku drugiej pochodnej, tj. jej miejsce zerowe (ang. zero crossing) obrazu może służyć do wyznaczenia miejsca wystąpienia brzegu. Wadą operatorów gradientowych jest uwypuklanie zakłóceń impulsowych w obrazach (może to powodować pogorszenie jakości obrazu lub detekcje fałszywych brzegów). 35

Gradient obrazu f(x, y) w punkcie (x, y) określa wektor: Wektor gradientu wskazuje kierunek największej zmiany jasności obrazu. Długość tego wektora nazywamy gradientem i obliczamy z zależności: 36

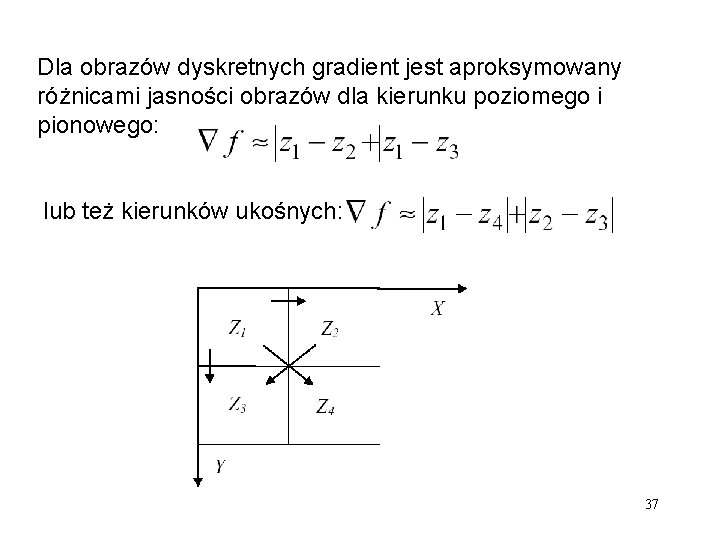
Dla obrazów dyskretnych gradient jest aproksymowany różnicami jasności obrazów dla kierunku poziomego i pionowego: lub też kierunków ukośnych: 37

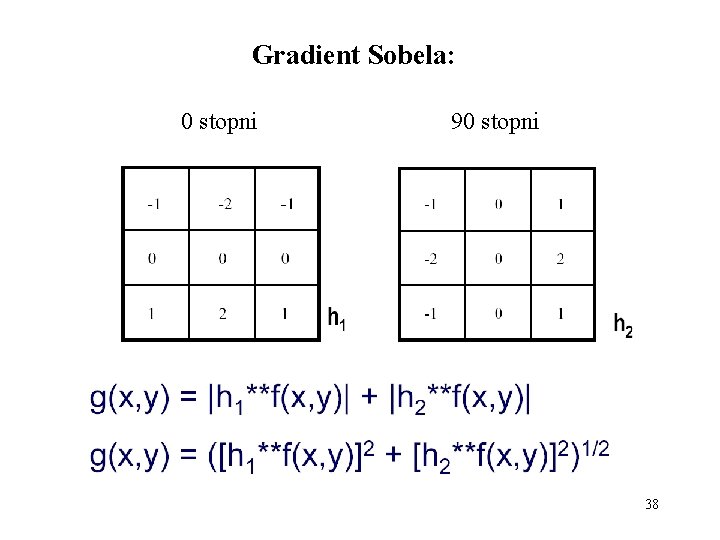
Gradient Sobela: 0 stopni 90 stopni 38

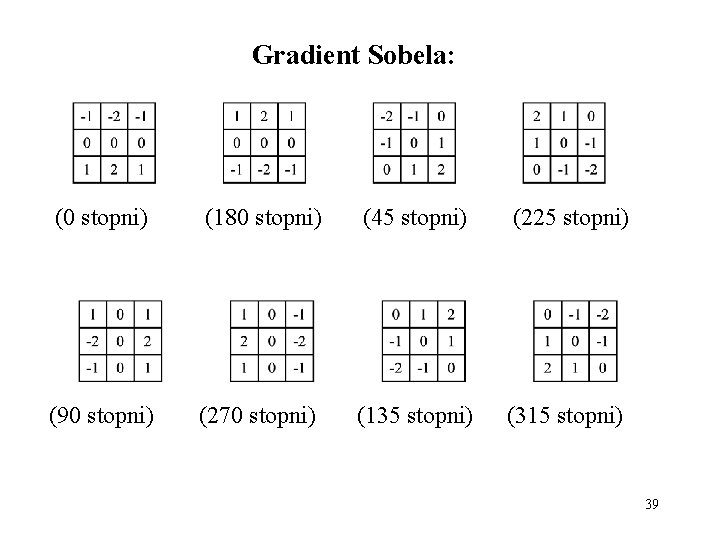
Gradient Sobela: (0 stopni) (180 stopni) (45 stopni) (225 stopni) (90 stopni) (270 stopni) (135 stopni) (315 stopni) 39

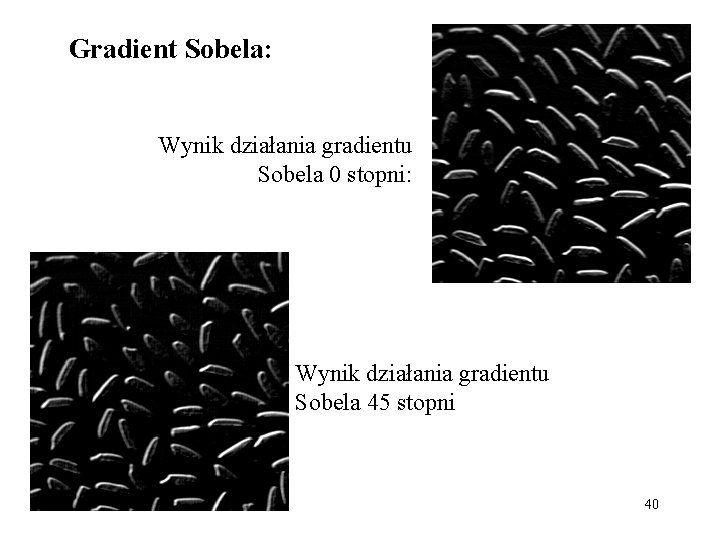
Gradient Sobela: Wynik działania gradientu Sobela 0 stopni: Wynik działania gradientu Sobela 45 stopni 40

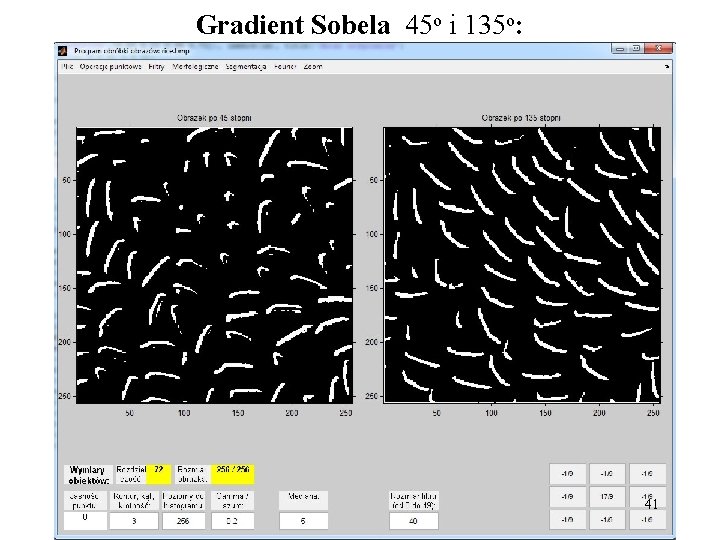
Gradient Sobela 45 o i 135 o: 41

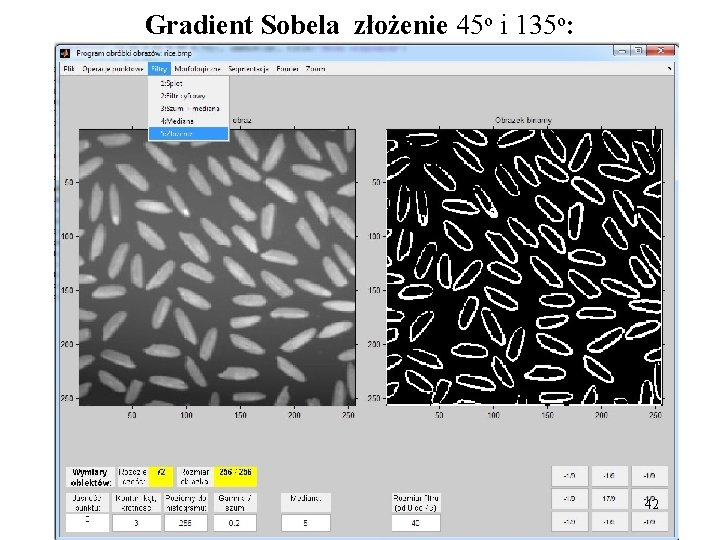
Gradient Sobela złożenie 45 o i 135 o: 42

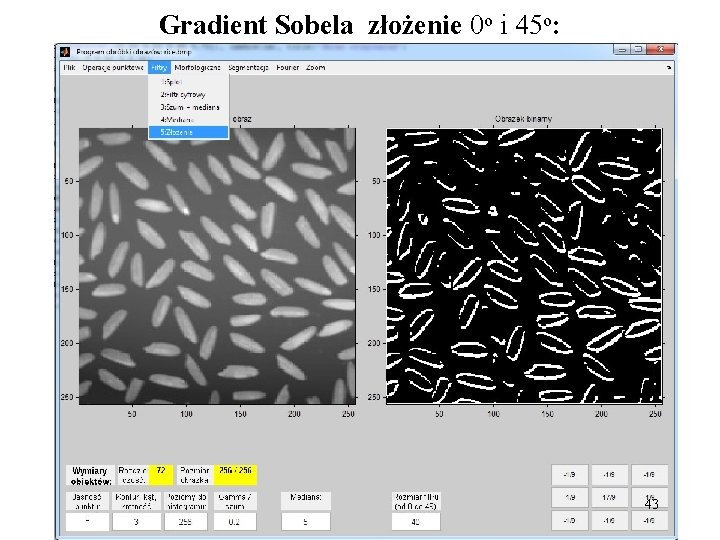
Gradient Sobela złożenie 0 o i 45 o: 43

Zapis programu: %h=[-1 -2 -1; 0 0 0; 1 2 1]; %h=[1 2 1; 0 0 0; -1 -2 -1]; h=[-2 -1 0; -1 0 1; 0 1 2]; %h=[2 1 0; 1 0 -1; 0 -1 -2]; im 2=filter 2(h, im); %h=[1 0 1; -2 0 2; -1 0 1]; %h=[1 0 -1; 2 0 -2; 1 0 -1]; h=[0 1 2; -1 0 1; -2 -1 0]; %h=[0 -1 -2; 1 0 -1; 2 1 0]; im 3=filter 2(h, im); im 4=sqrt(im 2. *im 2+im 3. *im 3); im 5=mat 2 gray(im 4); minimum=min(im 5)) maksimum=max(im 5)) 44

Zapis programu cd. : subplot('position', [0. 53 0. 22 0. 45 0. 73]), imshow(im 5), title('Obrazek po złożeniu i normalizacji') gr=graythresh(im 5) sr=mean 2(im 5) st=std 2(im 5) bw=im 2 bw(im 5, sr+st); pause(1) subplot('position', [0. 03 0. 22 0. 45 0. 73]); imshow(bw), title('Obrazek binarny') pause(1) subplot('position', [0. 03 0. 22 0. 45 0. 73]), imshow(im); title('Wprowadzony obraz') subplot('position', [0. 53 0. 22 0. 45 0. 73]); imshow(bw), title('Obrazek binarny') 45

Gradient Prewitta: (0 stopni) (180 stopni) (45 stopni) (225 stopni) (90 stopni) (270 stopni) (135 stopni) (315 stopni) 46

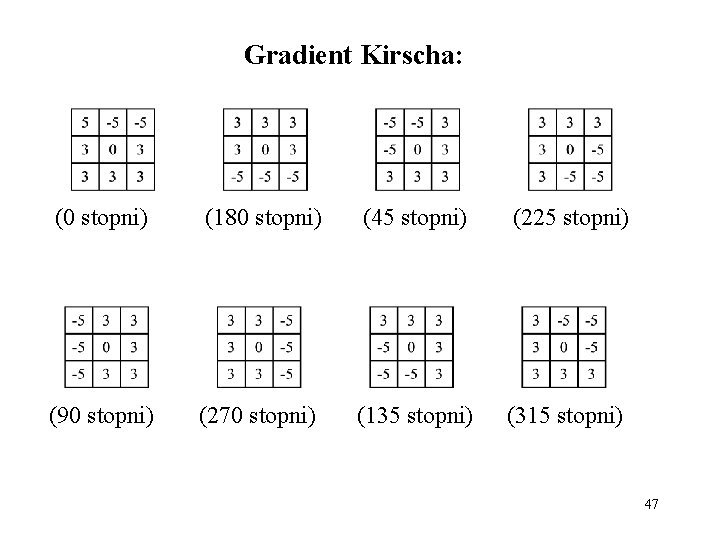
Gradient Kirscha: (0 stopni) (180 stopni) (45 stopni) (225 stopni) (90 stopni) (270 stopni) (135 stopni) (315 stopni) 47

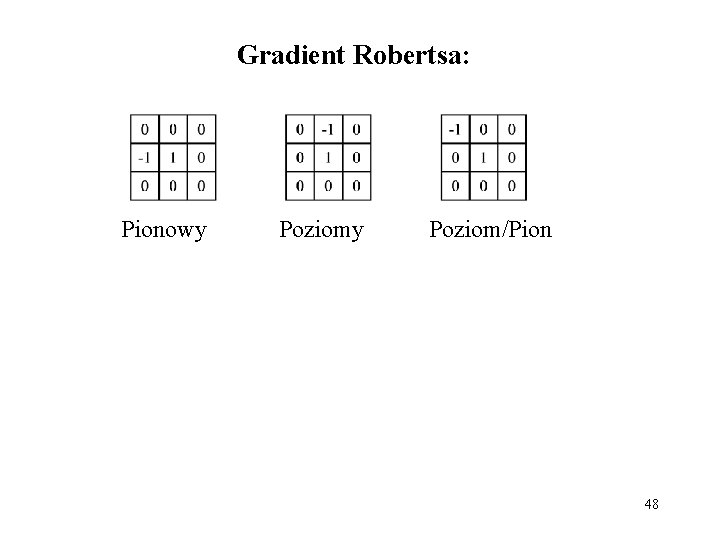
Gradient Robertsa: Pionowy Poziom/Pion 48

49

50

51

Analiza obrazów: • metody segmentacji obrazu (obraz binarny); • pomiar obiektów i ich kształtu (współczynniki kształtu, momenty geometryczne); • wymiar fraktalny; • szkieletyzacja; • operacje morfologiczne na obrazach binarnych oraz w skali szarości. 52

Miejsce segmentacji w procesie rozpoznawania 53

Obraz po segmentacji powinien mieć następujące cechy: • Obraz, powinien być jednorodny i jednolity (nie dotyczy to tekstur); • Wnętrza obszarów powinny być proste bez wielu małych otworów; • Obszary przylegające (graniczące ze sobą) do siebie powinny mieć inne wartości; • Brzegi obszarów powinny być proste, nie poszarpane. 54

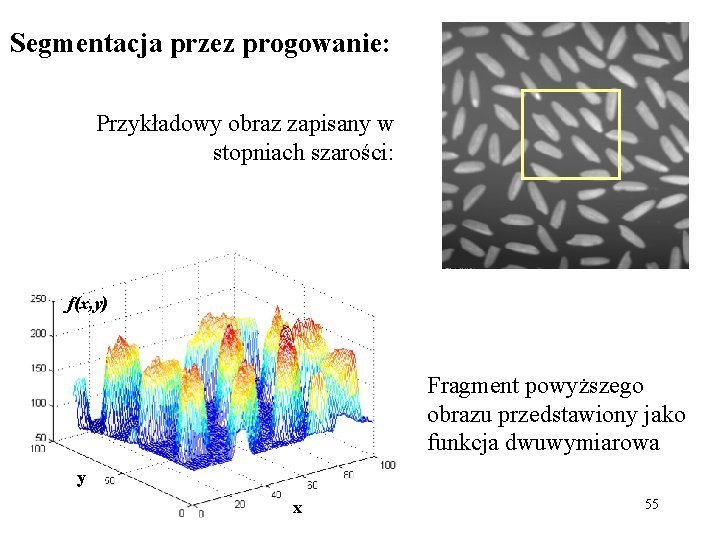
Segmentacja przez progowanie: Przykładowy obraz zapisany w stopniach szarości: f(x, y) Fragment powyższego obrazu przedstawiony jako funkcja dwuwymiarowa y x 55

Segmentacja przez progowanie cd. : Segmentacja obrazu ryżu z progiem 100: Rozciągnięty histogram oryginalnego obrazu ryżu 56

Inne przykłady segmentacji przez progowanie: 57

Inne przykłady segmentacji przez progowanie: 58

Inne przykłady segmentacji przez progowanie: 59

Inne przykłady segmentacji przez progowanie: 60

Przykłady nieudanej segmentacji przez progowanie: próg 40 próg 55 próg 75 próg 110 próg 120 próg 130 61

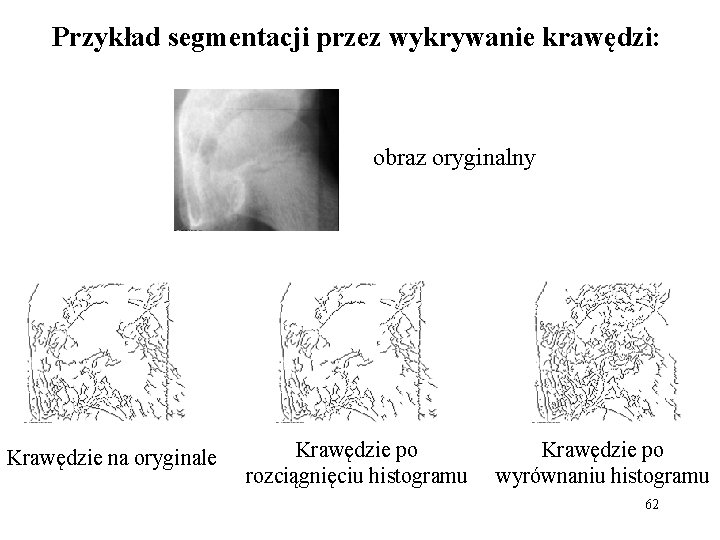
Przykład segmentacji przez wykrywanie krawędzi: obraz oryginalny Krawędzie na oryginale Krawędzie po rozciągnięciu histogramu Krawędzie po wyrównaniu histogramu 62

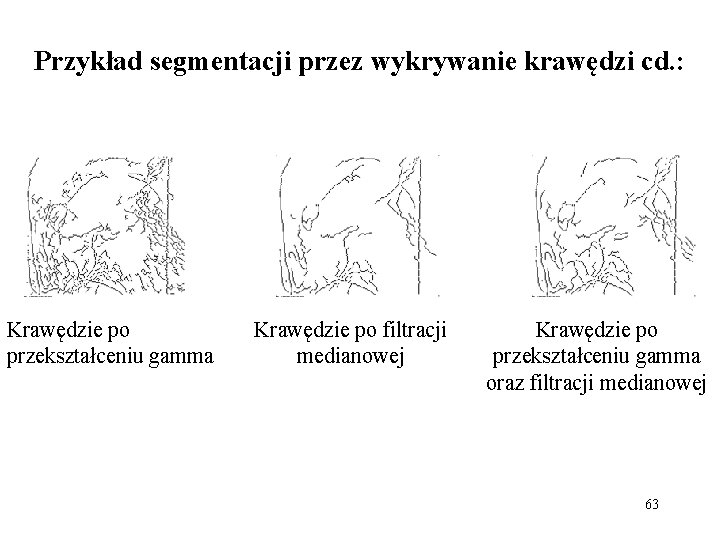
Przykład segmentacji przez wykrywanie krawędzi cd. : Krawędzie po przekształceniu gamma Krawędzie po filtracji medianowej Krawędzie po przekształceniu gamma oraz filtracji medianowej 63