Propositional Logic 1 Propositions A propositionis a declarative

Propositional Logic 1

Propositions A propositionis a declarative sentence that is either true or false. Examples of propositions: The Moon is made of green cheese. Trenton is the capital of New Jersey. Toronto is the capital of Canada. 1+0=1 0+0=2 Examples that are not propositions. Sit down! What time is it? x+1=2 x+y=z 2

Propositional Logic (or Calculus) Constructing Propositions Propositional Variables: p, q, r, s, … The proposition that is always true is denoted by T and the proposition that is always false is denoted by F. Compound. Propositions: constructed from other propositions using logical connectives Negation ¬ Conjunction ∧ Disjunction ∨ Implication → Biconditional ↔ 3

Compound Propositions: Negation The negationof a proposition p is denoted by ¬p and has this truth table: p ¬p T F F T Example: If p denotes “The earth is round” then ¬p denotes “It is not the case that the earth is round, ” or more simply “The earth is not round. ” 4

Conjunction The conjunctionof propositions p and q is denoted by p ∧ q and has this truth table: p q p∧q T T F F F T F F Example: If p denotes “I am at home” and q denotes “It is raining” then p ∧q denotes “I am at home and it is raining. ” 5

Disjunction The disjunctionof propositions p and q is denoted by p ∨q and has this truth table: p q p ∨q T T F F F Example: If p denotes “I am at home” and q denotes “It is raining” then p ∨q denotes “I am at home or it is raining. ” 6

The Connective Or in English In English “or” has two distinct meanings. Inclusive. Or: For p ∨q to be T, either p or q or both must be T Example: “CS 202 or Math 120 may be taken as a prerequisite. ” Meaning: take either one or both Exclusive Or (Xor). In p⊕q , either p or q but not bothmust be T Example: “Soup or salad comes with this entrée. ” Meaning: do not expect to get both soup and salad p q p ⊕q T T F T F T T F F F 7

Implication If p and q are propositions, then p →q is a conditional statementor implication, which is read as “if p, then q ” p is the hypothesis (antecedent or premise ) and q is the conclusion (or consequence ). p q p →q T T F F F T T F F T Example: If p denotes “It is raining” and q denotes “The streets are wet” then p →q denotes “If it is raining then streets are wet. ” 8

Understanding Implication In p →q there does not need to be any connection between p and q. The meaning of p →q depends only on the truth values of p and q. Examples of valid but counterintuitiveimplications: “If the moon is made of green cheese, then you have more money than Bill Gates” -- True “If Juan has a smartphone, then 2 + 3 = 6” -- False if Juan does have a smartphone, True if he does NOT 9

Understanding Implication View logical conditional as an obligationor contract: “If I am elected, then I will lower taxes” “If you get 100% on the final, then you will earn an A” If the politician is elected and does not lower taxes, then he or she has broken the campaign pledge. Similarly for the professor. This corresponds to the case where p is T and q is F. 10

Different Ways of Expressing p →q if p, then q if p, q p impliesq q if p q wheneverp q q p p q follows fromp unless ¬p only if q is sufficient forq is necessary forp Note: (p only if q) ≡ (q if p) ≢ (q only if p) It is raining → streets are wet: T It is raining only if streets are wet: T Streets are wet if it is raining: T Streets are wet only if it’s raining: F 11

Sufficient versus Necessary Example 1: p →q : get 100% on final → earn A in class p is sufficientfor q: getting 100% on final is sufficient for earning A q is necessaryfor p: earning A is necessary for getting 100% on final Counterintuitivein English: “Necessary” suggests a precondition Example is sequential Example 2: Nobel laureate → is intelligent Being intelligent is necessaryfor being Nobel laureate Being a Nobel laureate is sufficientfor being intelligent (better if expressed as: implies) 12

Converse, Inverse, and Contrapositive From p →q we can form new conditional statements. q →p is the converseof p →q ¬p→¬q is the inverse of p →q ¬q → ¬ p is the contrapositive of p →q How are these statements related to the original? How are they related to each other? Are any of them equivalent? 13

Converse, Inverse, and Contrapositive Example: it’s raining → streets are wet 1. converse: streets are wet → it’s raining 2. inverse: it’s not raining → streets are not wet 3. contrapositive: streets are not wet → it’s not raining only 3 is equivalent to original statement 1 and 2 are not equivalent to original statement: streets could be wet for other reasons 1 and 2 are equivalent to each other 14

Biconditional If p and q are propositions, then we can form the biconditionalproposition p ↔q, read as “p if and only if q ” p q p ↔q T T F F F T Example: If p denotes “You can take a flight” and q denotes “You buy a ticket” then p ↔q denotes “You can take a flight if and only if you buy a ticket” True only if you do both or neither Doing only one or the other makes the proposition false 15

Expressing the Biconditional Alternative ways to say “p if and only if q”: p is necessary and sufficient for q if p then q, and conversely p iff q 16

Compound Propositions conjunction, disjunction, negation, conditionals, and biconditionals can be combined into arbitrarily complex compound proposition Any proposition can become a term inside another proposition Propositions can be nested arbitrarily Example: p, q, r, t are simple propositions p ∨q , r ∧t , r →t are compound propositions using logical connectives (p ∨q) ∧ t and (p ∨q) →t are compound propositions formed by nesting 17

Precedence of Logical Operators With multiple operators we need to know the order To reduce number of parentheses use precedence rules Operator Precedence 1 2 3 4 5 Example: • p ∨q → ¬ r is equivalent to (p ∨q) → ¬ r • If the intended meaning is p ∨(q → ¬ r ) then parentheses must be used 18

Truth Tables of Compound Propositions Construction of a truth table: Rows One for every possible combination of values of all propositional variables Columns One for the compound proposition (usually at far right) One for each expression in the compound proposition as it is built up by nesting 19

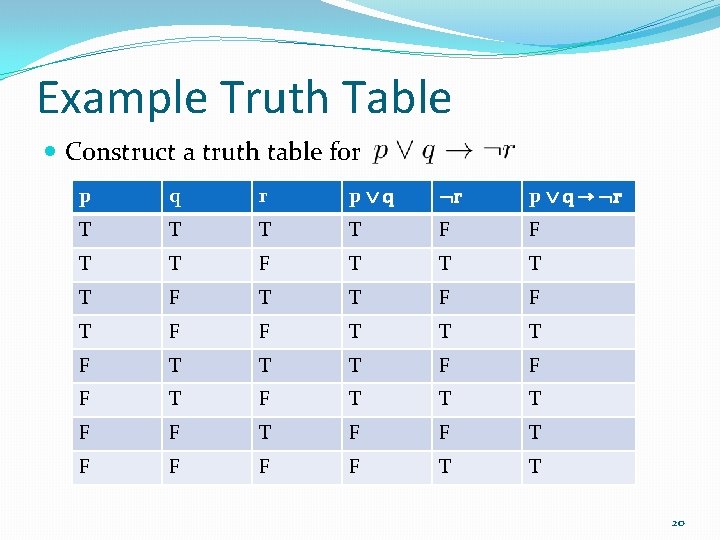
Example Truth Table Construct a truth table for p q r p q → r T T F F T T T T F F T T T F F F T T T F F T T 20