Logic Overview l l Scholastic logic Propositional logic

Logic

Overview l l Scholastic logic Propositional logic – – l Predicate calculus – – l l Syntax and semantics Inference rules Syntax and semantics Quantifiers Higher-order logics and modal operators Model theory – – The incremental, almost continuous nature of meaning Knowledge representation as an evolutionary process

Features of Logic KR Languages l Vocabulary – – l l Syntax Semantics – – l Logical symbols Constants Variables Punctuation Theory of reference Theory of truth Rules of inference

Automated Reasoning l Premise: Given an appropriate KR language, new knowledge can be inferred from existing truths

Syllogisms l Aristotle set out the concept of a threesentence structure to represent knowledge All trailer trucks are 18 wheelers Some Peterbilt is a trailer truck Therefore, some Peterbilt is an 18 Wheeler

Sentence Types l l A: Universal affirmative – All a is b I: Particular affirmative – Some a is b E: Universal negative – No a is b O: Particular negative – Some a is not b

Valid Syllogisms l b. Ar. A – – – A: All broad-leafed plants are deciduous A: All vines are broadleaf plants A: Therefore, all vines are deciduous

Valid Syllogisms (cont. ) l c. El. Ar. Ent – – – E: Nothing absent-minded is an elephant A: All professors are absent-minded E: Therefore, no professor is an elephant

Valid Syllogisms (cont. ) l d. Ar. II – – – A: All trailer trucks are 18 wheelers I: Some Peterbilt is a trailer truck I: Therefore, some Peterbilt is an 18 Wheeler

Valid Syllogisms (cont. ) l f. Er. IO – – – E: No Corvette is a truck I: Some Chevrolet is a Corvette O: Therefore, some Chevrolet is not a truck

Boolean Algebra l l George Boole System of representing and operating on truth values pxq p+q -p AND OR NOT

First Order Logic (FOL) l Extensions of Boolean Algebra and Aristotle’s syllogisms – – Universal and existential quantifiers Changes in syntax

Why FOL? l l l Expressive power Extensive Semantics Best-defined model and proof theories

Syntax of Propositional Logic l Symbols – – – Logical constants True, False Proposition symbols: P, Q, … Logical connectives: l l l not (aka “? ”) and (aka “? ”) or (aka “? ”) => (aka “? ”) iff (aka “? ”) Sentences are made from these symbols

Sentences l l l True, False are sentences Any proposition symbol is a sentence Any sentences S 1, … Sn combined with a connective is a sentence – – – (not S) is a sentence (and S 1 S 2) is a sentence (or S 1 S 2 S 3 … Sn) is a sentence (=> Sa Sc) is a sentence (iff Sa Sc) is a sentence

Semantics of propositional logic l Formal semantics = function from sentences to true, false. – – l True means that the sentence is true of the world False means that the sentence isn’t true of the world Truth tables define semantics of connectives – – See Sowa for details Example P false true Q false true (or P Q) false true

Rules of Inference: Examples 1. Modus Ponens (aka implication-elimination) – 2. And-elimination – 3. Given P, Q, infer (and P Q) Unit resolution – 5. Given (and P Q), infer P; or infer Q And-introduction – 4. Given (=> P Q), P, infer Q Given (or P Q), (not P), infer Q Resolution – Given (or P Q), (or (not Q) R), infer (or P R)

Using inference rules l “On summer days in Memphis, it is either scorching hot or overcast and muggy outside. Today is a summer day in Memphis and it is not scorching hot outside. ”

Formalizing a situation “On summer days in Memphis, it is either scorching hot or overcast and muggy outside. Today is a summer day in Memphis and it is not scorching hot outside. ” l Summer = “It is a summer day in Memphis” l Hot = “It is scorching hot outside” l Overcast = “It is overcast outside” l Muggy = “It is muggy outside” (=> Summer (or Hot (and Overcast Muggy))) (and Summer (not Hot))

Using the Inference Rules 1. 2. 3. 4. 5. 6. 7. 8. (=> Summer (or Hot (and Overcast Muggy))) Given (and Summer (not Hot )) Given Summer [AE 2] (or Hot (and Overcast Muggy)) [MP 1, 3] (not Hot) [AE 2] (and Overcast Muggy) [UR 4, 5] Overcast [AE 6] Muggy [AE 6]

Properties of inference rules l l l They are sound if, when the premises are true, the consequence is true Many different sets of inference rules have been created with the same expressive power (i. e. , complete) Sometimes restricted sets of inference rules used for tractability – Example: Horn clauses (=> (and A 1 … An) C)

Predicate Calculus l Propositions can have structure: (<predicate>. <terms>) l Terms are either – – l l Constants denoting objects in some universe (e. g. , Block 32) Expressions denoting objects via a function (e. g. , (color Block 32)) Predicates describe attributes and relationships Examples: (Red Block 32) (On Block 32 Table) (Above Block 24 Block 32)

Propositions express facts l Concrete facts via appropriate vocabulary of relationships – l Describing general facts of the world requires variables – l Example: The things sitting on top of a table We’ll use ? <symbol> to denote variables. The meaning of variables are defined via quantifiers

Universal Quantification l (forall <vars> <sentence>) is true exactly when <sentence> is true for every possible set of bindings for <vars> – Examples: (forall ? x (=> (block ? x) (solid-object ? x))) (forall (? x ? y) (=> (and (person ? x) (person ? y) (friend-of ? x ? y)) (friend-of ? y ? x)))

Inference with universal quantifiers l Elimination via substitution – (forall ? x (=> (block ? x) (solid-object ? x))), Let ? x=Block 32 (=> (block Block 32) (solid-object Block 32)) l Introduction by proving statement for an arbitrary individual about which nothing else is known (a skolem) – (=> (even-number Foobar) (not (prime-number Foobar)))

Existential Quantification l (exists <varlist> <sentence>) is true exactly when there is at least one set of bindings for <varlist> that make <sentence> true. l Examples – (for-all ? x (=> (number ? x) (exists ? y (> ? y ? x)))) (for-all ? x (=> (block ? x) (or (on ? x table) (held ? x) (exists ? y (and (block ? y) (on ? x ? y))))))

Using existential quantifiers l Elimination by creating a skolem. – l (exists ? y (and (block ? y) (on Block 32 ? y))) create novel entity, G 0012, and substitute: (and (block G 0012) (on Block 32 G 0012)) Introduction by generalizing from a specific example (and (block Block 18)(on Block 32 Block 18)) justifies the introduction of (exists (? x ? y) (and (block ? x) (on ? y ? x)))

Tips for using quantifiers l Be very careful of scoping when translating from natural language – l “Wherever you go, there you are” B. Banzi Heuristic: Use => inside forall (forall ? x (and (block ? x) (solid-object ? x))) l Heuristic: Use and inside exists (? x ? y) (=> (block ? x) (on ? x ? y))) l Heuristic: Use iff very sparingly (forall ? x (iff (block ? x) (solid-object ? x))

Higher-order logic l l First order logic ? variables range over objects Second order logic ? variables can range over predicates also (for-all ? r (iff (transitive ? r) (forall (? x ? y ? x) (=> (and (? r ? x ? y) (? r ? y ? z)) (? r ? x ? z))))) l l Omega-order logics have been used at times Even second order is undecidable, however

Aside: Order in Structure-Mapping l Not the same thing as the order of a logic – l In structure-mapping, the order of an expression is – – l Order of a logic indicates how expressive it can be 0 for entities 1+max(order(arguments)) for expressions Order of an expression indicates the degree of nesting

Types of Logic l Variations of FOL – – – Syntax Subsets Proof theory Model theory Ontology Metalanguage

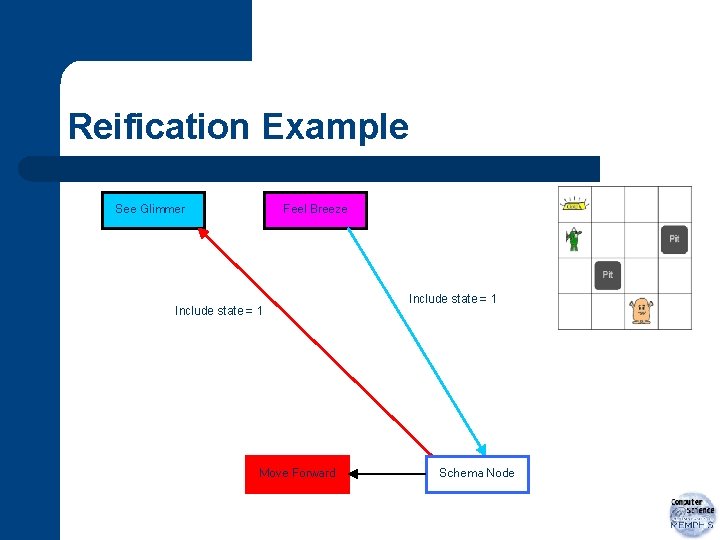
Reification l Formal trick: – For each predicate, create a constant that stands for it l l – – l In KIF, it is the tuple semantics of the predicate Requires an axiom schema (think “macro”) Use those constants in axioms Since they are constants, the resulting theory is first-order Useful for expressing control knowledge – Reify facts, so one can say when they are relevant

Reification Example See Glimmer Feel Breeze Include state = 1 Move Forward Include state = 1 Schema Node

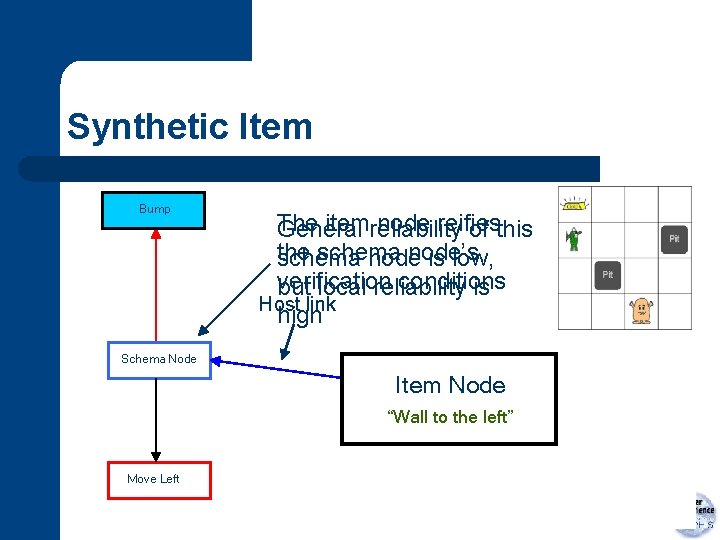
Synthetic Item Bump The itemreliability node reifies General of this the schema node’s schema node is low, verification conditions but local reliability is Host link high Schema Node Item Node “Wall to the left” Move Left

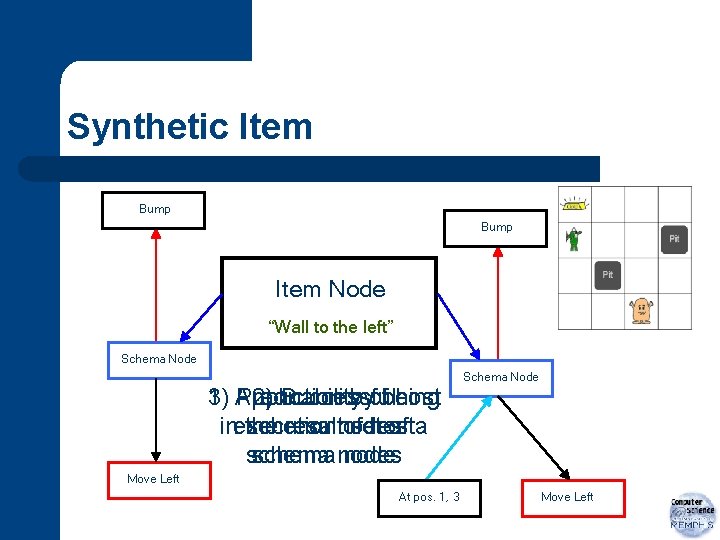
Synthetic Item Bump Item Node “Wall to the left” Schema Node Context spin-offs Item Node 1) 3) Applicability Prediction 2) Successful byofbeing host refine the verification “Wall to the left” inexecution the schema result nodes of set host of a conditions schema nodes node Move Left At pos. 1, 3 Move Left

Modal Operators l Modal operators extend the expressive power of a logic by specifying context – – l Classic examples from logic: (necessary P), (possible P) – l Metaphor: quotation and backquote Can use reification of their semantics to drop the reasoning to first order, but can still be hairy (iff (necessary P) (not (possible (not P)))) Classic examples from AI/Philosophy: (Knows A P), (Believes A P) (=> (knows John (visible morning-star)) (knows John (visible evening-star)))

Model Theory l Meaning of a theory = set of models that satisfy it. – – – l Model = set of objects and relationships If statement is true in KB, then the corresponding relationship(s) hold between the corresponding objects in the modeled world The objects and relationships in a model can be formal constructs, or pieces of the physical world, or whatever Meaning of a predicate = set of things in the models for that theory which correspond to it. – E. g. , above means “above”, sort of

Caution: Meaning pertains to simplest model l l There is usually an intended model, i. e. , what one is representing. A sparse set of axioms can be satisfied by dramatically simpler worlds than those intended – Example: Classic blocks world axioms have ordered pairs of integers as a model l l (<position on table> <height>) ? block (on A B) ? p(A) = p(B) & h(A) = h(B)+1 (above A B) ? p(A) = p(B) & h(A) > h(B) Moral: Use dense, rich set of axioms and make sure you are defining what you think you are defining

Misconceptions about meaning l “Predicates have definitions” – l Most don’t. Their meaning is constrained by the sum total of axioms that mention them. “Logic is too discrete to capture the dynamic fluidity of how our concepts change as we learn” – – If you think of the set of axioms that constrain the meaning of a predicate as large, then adding (and removing) elements of that set leads to changes in its models. Sometimes small changes in the set of axioms can lead to large changes in the set of models. This is the logical version of a discontinuity.

Representations as Sculptures l How does one make a statue of an elephant? – l How does one represent a concept? – l Start with a marble block. Carve away everything that does not look like an elephant. Start with a vocabulary of predicates and other axioms. Add axioms involving the new predicate until it fits your intended model well. Knowledge representation is an evolutionary process – – It isn’t quick, but incremental additions lead to incremental progress All representations are by their nature imperfect