Probability Distributions WW Chapter 4 Discrete Random Variables

Probability Distributions W&W Chapter 4

Discrete Random Variables Suppose a couple plan to have 3 children and are interested in the number of girls they might have. This is an example of a random variable, and is denoted by a capital letter: X = the number of girls The possible values of X are 0, 1, 2, and 3; however they are not equally likely.

Discrete Random Variables We need to calculate X Pr(X) 0 1 2 3

Discrete Random Variables Using Pr(boy)=. 52 and Pr(girl)=. 48 e BBB BBG BGB BGG GBB GBG GGB GGG Pr(e). 14. 13. 12. 11 x 0 p(x). 14 1 . 39 (. 13+. 13) 2 . 36 (. 12+. 12) 3 . 11 Pr(x)=1

Discrete Random Variables A discrete random variable takes on various values x with probabilities specified by its probability distribution, p(x).
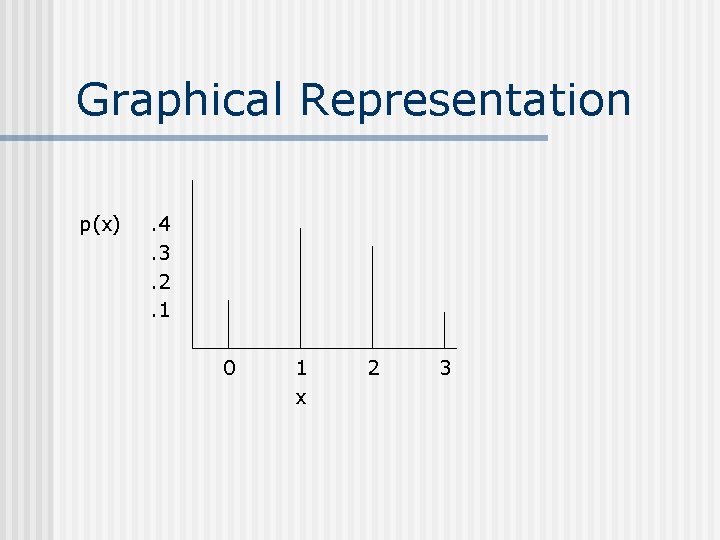
Graphical Representation p(x) . 4. 3. 2. 1 0 1 x 2 3

Example What is the probability of fewer than two girls? Pr(X<2) = p(0) + p(1) =. 14 + 39 =. 53

Notation X: random variable x: a specific value that X may take p(0), p(1), . . p(x) are the probabilities of x Example: the probability of having one girl in a family of three, Pr(X=1) or just p(1) A random variable can be discrete or continuous.

Mean and Variance Previously we learned how to calculate the mean and variance for a sample as follows: Xbar = X/N s 2 = (X- Xbar)2/(N-1)

Population Mean and Variance We can calculate the mean and variance of a random variable from its probability distribution, p(x): Mean: = xp(x) Variance: 2 = (x- )2 p(x) Remember that Greek letters denote population statistics!

Variance We can rewrite the formula for variance as follows: 2 = x 2 p(x) - 2 Start with 2 = (x- )2 p(x) = (x 2 - 2 x + 2) p(x) and noting that is a constant: 2 = x 2 p(x) - 2 x p(x) + 2 p(x) Since x p(x) = and p(x) = 1, 2 = x 2 p(x) - 2 ( ) + 2(1) = x 2 p(x) - 2

Example Let’s calculate the mean and variance of the random variable X, the number of girls Mean = xp(x) = (0)(. 14) + (1)(. 39) + (2)(. 36) + (3)(. 11) = 1. 44 2 = (x- )2 p(x) = (0 -1. 44)2(. 14)+ (11. 44)2(. 39) + (2 -1. 44)2(. 36) + (31. 44)2(. 11) = 0. 7464

Interpretation The mean number of girls in a family of 3 is 1. 44 and the variance is about. 75. Notice that 1. 44/3 =. 48, which is the relative frequency (f/n) for girls! and 2 have similar interpretations to the sample mean and variance. is a weighted average using probability weights rather than relative frequency weights, and the standard deviation ( ) is the typical deviation

Factorials Question: Suppose you have 3 shirts, 2 sweaters, and 2 pairs of pants. How many outfits can you form? If we imagine a decision tree, we will find that the answer is 12. This can be derived by 3 2 2 = 12

Factorials (continued) Rule of counting: A number of multiple choices are to be made. There are m 1 possibilities for the first choice, m 2 for second, and so on. If these choices can be combined freely, then the total number of possibilities for the whole set of choices is m 1 m 2 m 3…

Factorials (continued) Suppose you have a survey questionnaire with n questions. How many ways are there to order the n questions? There are n ways to choose the first question, but after deciding this one, there are only n-1 ways to choose the second, n-2 ways to choose third and so on. Thus the number is n(n-1)(n-2) 2 1, which we call n factorial, or n! for short.

The Binomial Distribution There are many types of discrete random variables and the most common is called the binomial. The classical example of a binomial variable is: S = number of heads in several tosses of a coin

Assumptions of the Binomial Distribution 1) We suppose there are n trials (tosses of the coin) 2) In each trial, a certain event of interest can occur or fail to occur; then we say a success (head) or failure (tail) has occurred. Their respective probabilities are and 1 - .

Assumptions (Continued) 3) We assume the trials are statistically independent (remember this means that the chances of getting a head on one flip are not influenced by getting a head or tail on a previous flip). 4) S is the total number of successes in n trials, and is called a binomial variable.

Examples of Binomial Variables Trial Success Failure Tossing a coin Head Tail n ½ # tosses Birth of a child Girl . 48 # children # girls Boy Multiple Choice Correct Wrong S # heads 1/5 # questions # correct Drawing a voter Rep. Dem/Other f/N # surveyed # Rep.

Probability Distribution for a Binomial Variable p(s) = ( n ) s (1 - )n-s ( s ) where ( n ) = n!/[s!(n-s)!] ( s ) and the factorial n! is given by n! = n(n-1)(n-2) 1

Example of the Binomial Recall that the probability of 1 girl, or p(1) in a family of 3 children was. 39. We can demonstrate that the binomial produces the same result. p(1) = (3)(. 48)1(. 52)3 -1 = (1) p(1) = (3 2 1)/[1(2 1)](. 48)(. 2704) = 3(. 129792) =. 39

Another Example Suppose we want to know if the chances for women receiving tenure at FSU are fair, so in this case S = number of women who receive tenure at FSU in a given year. We assume that if everyone has an equal chance for tenure, then the proportion of women that have tenure should be close to the proportion of women hired as assistant professors. We collect this information for 15 years and determine that: =. 4 and 1 - =. 6

Example (continued) We count the number of tenured faculty by gender and come up with the following data: #female = 25 and #male = 75. What is the probability that the tenure process is fair? S = 25 females tenured p(s) = (100)(. 4)25(. 6)75 (25) p(s) =. 0006 We conclude that if the process were fair, the chances of getting only 25% of women tenured given hiring rates is highly unlikely.

Sampling from a large population Recall the example of light bulbs which demonstrated how sampling without replacement can change the probability for successive draws. If we draw one card out of a deck of cards, the probability for getting a particular card on the second draw changes because we have removed the first card. But in really large populations, we can act as though the removal does not matter.

Example Suppose that a production run of 40, 000 microwave ovens includes 32, 000 (80%) that are flawless. But the quality control department, not knowing this figure, takes a random sample of 10 to estimate the overall quality. What is the chance that the sample will be evenly split, 5 flawless and 5 not?

Example Each of the 10 successive ovens in the sample can be considered a trial, so n = 10. Now in this case, removing one good oven will change the probability of getting a good one on the next draw (even though the binomial assumes independence). For the first oven, the probability of success (flawless) is 32, 000/40, 000 =. 8. If the first oven was a success, then the probability of success is 31, 999/39, 999; if it was a failure, then the probability of success on the second draw is 32, 000/39, 999. But this comes out very close to. 8. So the second trial is practically independent of the first, and we can use the binomial.

Example p(5) = (10)(. 80)5(. 20)5 (5) = 252(. 000105) =. 026 That is, in a random sample of 10 ovens, there is close to a 3% chance that 5 will be flawless and 5 will not. We must emphasize the most important assumption of the binomial distribution, which is that the trials are independent. For smaller samples where the trials are dependent on each other, the binomial would not be appropriate.
- Slides: 28




















































