Chapter 5 Discrete Probability Distributions Random Variables Discrete

Chapter 5 Discrete Probability Distributions Random Variables Discrete Probability Distributions Expected Value and Variance Binomial Probability Distribution Poisson Probability Distribution Hypergeometric Probability Distribution. 40. 30. 20. 10 0 1 2 3 4

Random Variables A random variable is a numerical description of the outcome of an experiment. A random variable can be classified as being either discrete or continuous depending on the numerical values it assumes. A discrete random variable may assume either a finite number of values or an infinite sequence of values. A continuous random variable may assume any numerical value in an interval or collection of intervals.

Example: JSL Appliances Discrete random variable with a finite number of values Let x = number of TV sets sold at the store in one day where x can take on 5 values (0, 1, 2, 3, 4) Discrete random variable with an infinite sequence of values Let x = number of customers arriving in one day where x can take on the values 0, 1, 2, . . . We can count the customers arriving, but there is no finite upper limit on the number that might arrive.
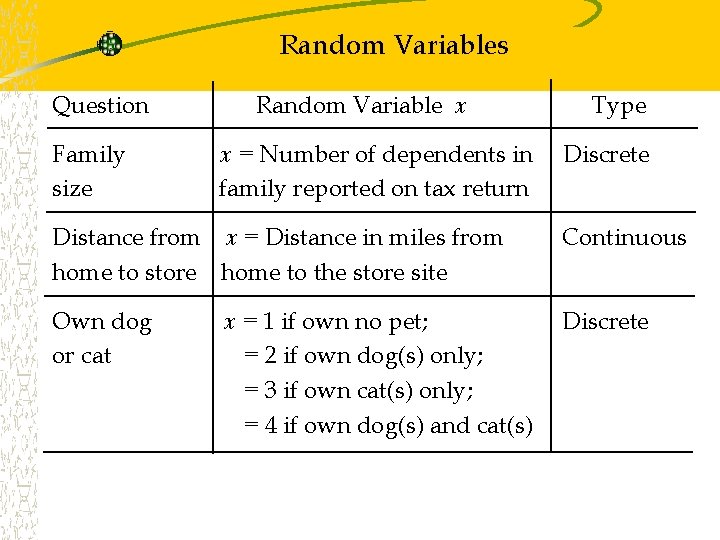
Random Variables Question Family size Random Variable x x = Number of dependents in family reported on tax return Type Discrete Distance from x = Distance in miles from home to store home to the store site Continuous Own dog or cat Discrete x = 1 if own no pet; = 2 if own dog(s) only; = 3 if own cat(s) only; = 4 if own dog(s) and cat(s)

Discrete Probability Distributions The probability distribution for a random variable describes how probabilities are distributed over the values of the random variable. The probability distribution is defined by a probability function, denoted by f(x), which provides the probability for each value of the random variable. The required conditions for a discrete probability function are: f(x) > 0 f(x) = 1 We can describe a discrete probability distribution with a table, graph, or equation.
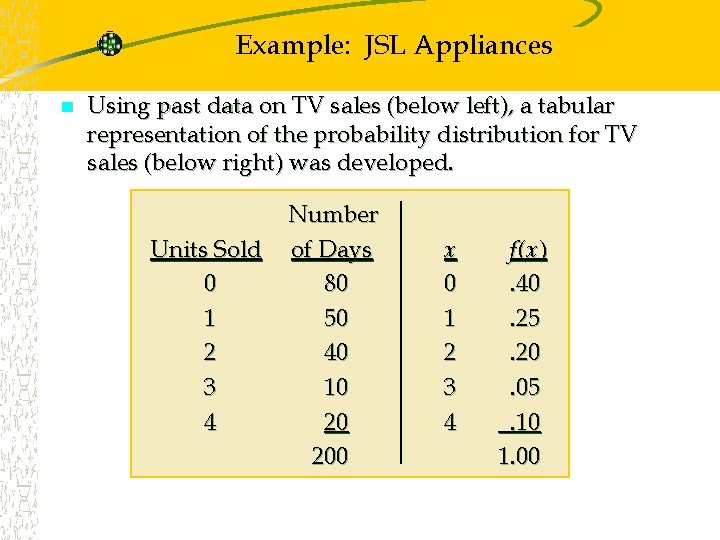
Example: JSL Appliances n Using past data on TV sales (below left), a tabular representation of the probability distribution for TV sales (below right) was developed. Units Sold 0 1 2 3 4 Number of Days 80 50 40 10 20 200 x 0 1 2 3 4 f (x ). 40. 25. 20. 05. 10 1. 00
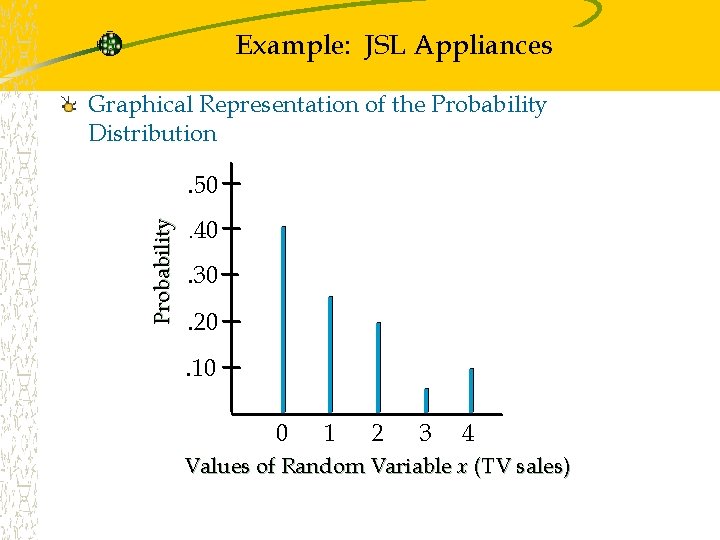
Example: JSL Appliances Graphical Representation of the Probability Distribution Probability . 50. 40 . 30. 20. 10 0 1 2 3 4 Values of Random Variable x (TV sales)

Discrete Uniform Probability Distribution The discrete uniform probability distribution is the simplest example of a discrete probability distribution given by a formula. The discrete uniform probability function is f(x) = 1/n where: n = the number of values the random variable may assume Note that the values of the random variable are equally likely.

Expected Value and Variance The expected value, or mean, of a random variable is a measure of its central location. E(x) = = xf(x) The variance summarizes the variability in the values of a random variable. Var(x) = 2 = (x - )2 f(x) The standard deviation, , is defined as the positive square root of the variance.

Example: JSL Appliances Expected Value of a Discrete Random Variable x 0 1 2 3 4 f(x) xf(x). 40. 00. 25. 20. 40. 05. 10. 40 E(x) = 1. 20 The expected number of TV sets sold in a day is 1. 2

Example: JSL Appliances Variance and Standard Deviation of a Discrete Random Variable x x- (x - )2 f(x) 0 1 2 3 4 -1. 2 -0. 2 0. 8 1. 8 2. 8 1. 44 0. 04 0. 64 3. 24 7. 84 . 40. 25. 20. 05. 10 (x - )2 f(x). 576. 010. 128. 162. 784 1. 660 = The variance of daily sales is 1. 66 TV sets squared. The standard deviation of sales is 1. 2884 TV sets.

Binomial Probability Distribution Properties of a Binomial Experiment 1. The experiment consists of a sequence of n identical trials. 2. Two outcomes, success and failure, are possible on each trial. 3. The probability of a success, denoted by p , does not change from trial to trial. 4. The trials are independent. Stationarity Assumption

Binomial Probability Distribution Our interest is in the number of successes occurring in the n trials. We let x denote the number of successes occurring in the n trials.

Binomial Probability Distribution Number of Experimental Outcomes Exactly x Successes in n Trials where: n! = n(n – 1)(n – 2). . . (2)(1) 0! = 1 Providing

Binomial Probability Distribution Probability of a Particular Sequence of Trial Outcomes with x Successes in n Trials

Binomial Probability Distribution Binomial Probability Function where: f(x) = the probability of x successes in n trials n = the number of trials p = the probability of success on any one trial

Example: Evans Electronics n Binomial Probability Distribution Evans is concerned about a low retention rate for employees. On the basis of past experience, management has seen a turnover of 10% of the hourly employees annually. Thus, for any hourly employees chosen at random, management estimates a probability of 0. 1 that the person will not be with the company next year. Choosing 3 hourly employees at random, what is the probability that 1 of them will leave the company this year?

Example: Evans Electronics Using the Binomial Probability Function Let: p =. 10, n = 3, x = 1 = (3)(0. 1)(0. 81) = . 243
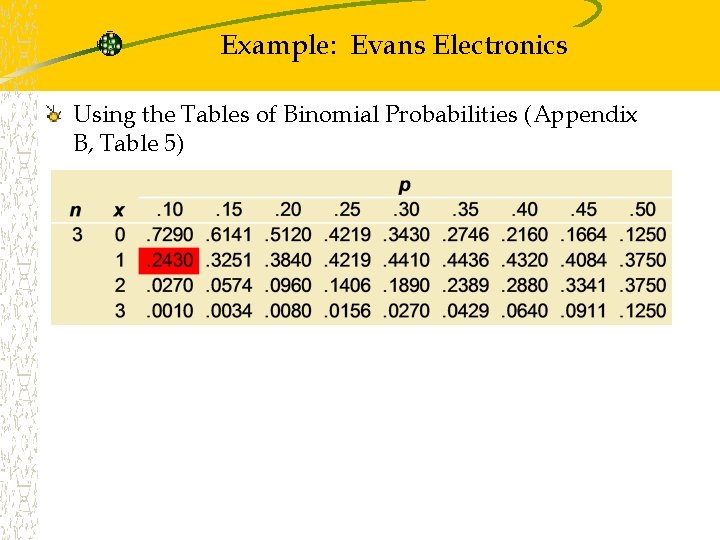
Example: Evans Electronics Using the Tables of Binomial Probabilities (Appendix B, Table 5)
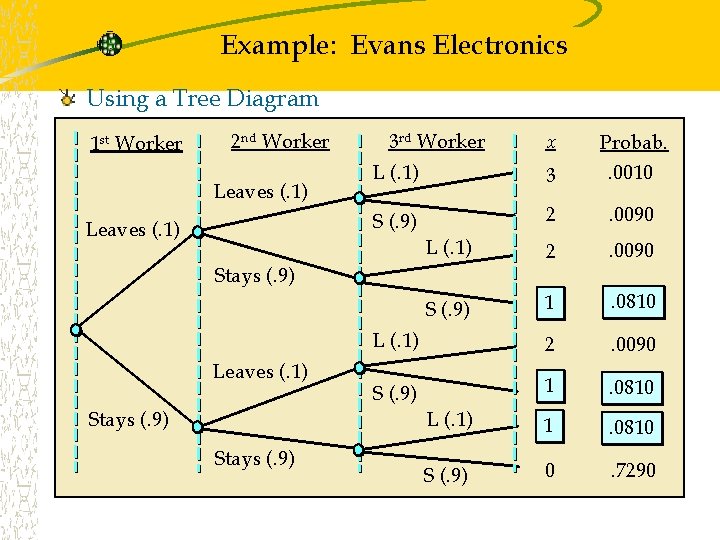
Example: Evans Electronics Using a Tree Diagram 1 st Worker 2 nd Worker Leaves (. 1) 3 rd Worker L (. 1) 3 Probab. . 0010 S (. 9) 2 . 0090 L (. 1) 2 . 0090 S (. 9) 1 . 0810 L (. 1) 1 . 0810 S (. 9) 0 . 7290 Stays (. 9) Leaves (. 1) Stays (. 9) x

Binomial Probability Distribution Expected Value E(x) = = np Variance Var(x) = 2 = np (1 - p ) Standard Deviation

Example: Evans Electronics Binomial Probability Distribution – Expected Value E(x) = = 3(. 1) =. 3 employees out of 3 – Variance Var(x) = 2 = 3(. 1)(. 9) =. 27 – Standard Deviation

Poisson Probability Distribution A discrete random variable following this distribution is often useful in estimating the number of occurrences over a specified interval of time or space. It is a discrete random variable that may assume an infinite sequence of values (x = 0, 1, 2, . . . ). Examples: – the number of customers arriving at a Mc. Donald restaurant in a 15 minutes interval – the number of vehicles arriving at a toll booth in one hour

Poisson Probability Distribution Properties of a Poisson Experiment – The probability of an occurrence is the same for any two intervals of equal length. – The occurrence or nonoccurrence in any interval is independent of the occurrence or nonoccurrence in any other interval.

Poisson Probability Distribution Poisson Probability Function where: f(x) = probability of x occurrences in an interval = mean number of occurrences in an interval e = 2. 71828

Example: Mercy Hospital Using the Poisson Probability Function Patients arrive at the emergency room of Mercy Hospital at the average rate of 6 per hour on weekend evenings. What is the probability of 4 arrivals in 30 minutes on a weekend evening? = 6/hour = 3/half-hour, x = 4
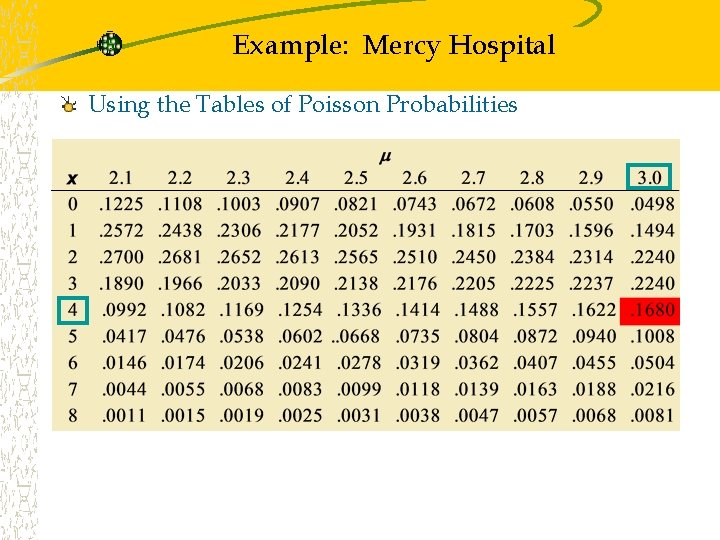
Example: Mercy Hospital Using the Tables of Poisson Probabilities

Hypergeometric Probability Distribution The hypergeometric distribution is closely related to the binomial distribution. The key differences are: – the trials are not independent – probability of success changes from trial to trial

Hypergeometric Probability Distribution Hypergeometric Probability Function for 0 < x < r where: f(x) = probability of x successes in n trials n = number of trials N = number of elements in the population r = number of elements in the population labeled success

Hypergeometric Probability Distribution Hypergeometric Probability Function – is the number of ways a sample of size n can be selected from a population of size N. – is the number of ways x successes can be selected from a total of r successes in the population. – is the number of ways n – x failures can be selected from a total of N – r failures in the population.

Example: Neveready Hypergeometric Probability Distribution Bob Neveready has removed two dead batteries from a flashlight and inadvertently mingled them with the two good batteries he intended as replacements. The four batteries look identical. Bob now randomly selects two of the four batteries. What is the probability he selects the two good batteries?

Example: Neveready Hypergeometric Probability Distribution where: x = 2 = number of good batteries selected n = 2 = number of batteries selected N = 4 = number of batteries in total r = 2 = number of good batteries in total

End of Chapter 5
- Slides: 33