Discrete Random Variables Discrete Probability Distributions Binomial Distribution

Discrete Random Variables Discrete Probability Distributions • Binomial Distribution • Poisson Distribution • Hypergeometric Distribution Econ 10/Mgt 10 Stuffler 1

Discrete Probability Distributions Discrete Random Variables – Sample Space includes all mutually exclusive outcomes Probabilities – from subjective, frequency or subjective methods Two conditions apply: Econ 10/Mgt 10 Stuffler 2

Discrete Probability Distributions Probability distributions can be estimated from relative frequencies. Consider the discrete (countable) number of televisions per household (millions) from US survey data: Econ 10/Mgt 10 Stuffler 3

Discrete Probability Distributions Probability distributions can be estimated from relative frequencies. Consider the discrete (countable) number of televisions per household from US survey data: 1, 218 ÷ 101, 501 = 0. 012 Econ 10/Mgt 10 Stuffler 4

Discrete Probability Distributions Probability distributions can be estimated from relative frequencies. Consider the discrete (countable) number of televisions per household from US survey data: EX: P(X=4) = P(4) = 0. 076 = 7. 6% Econ 10/Mgt 10 Stuffler 5
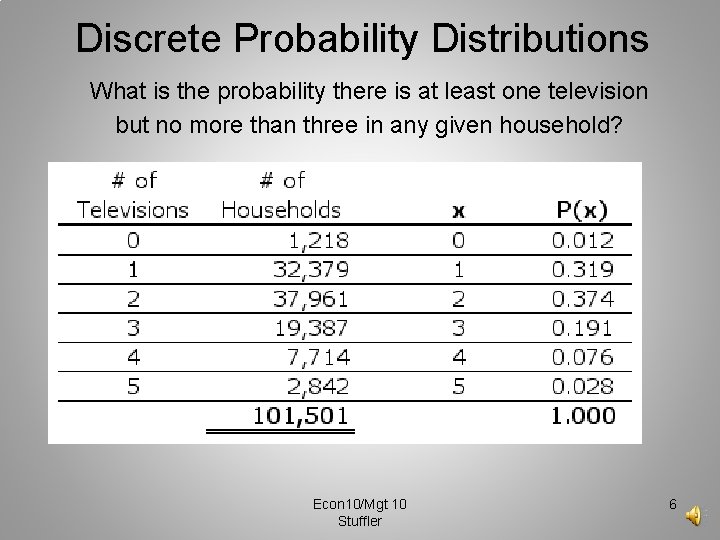
Discrete Probability Distributions What is the probability there is at least one television but no more than three in any given household? Econ 10/Mgt 10 Stuffler 6

Discrete Probability Distributions What is the probability there is at least one television but no more than three in any given household? Econ 10/Mgt 10 Stuffler 7

Discrete Probability Distributions What is the probability there is at least one television but no more than three in any given household? “at least one television but no more than three” P(1 ≤ X ≤ 3) = P(1) + P(2) + P(3) =. 319 +. 374 +. 191 =. 884 Econ 10/Mgt 10 Stuffler 8

Discrete Probability Distributions Assume a mutual fund salesman knows that there is 20% chance of closing a sale on each call he makes. Econ 10/Mgt 10 Stuffler 9

Discrete Probability Distributions What is the probability distribution of the number of sales if he plans to call three customers? Let S denote success, making a sale: P(S) =. 20, then Sʹ, not making a sale: P(Sʹ) =. 80 Econ 10/Mgt 10 Stuffler 10

Discrete Probability Distributions • Developing a Probability Distribution Tree Sales Call 1 P(S)=. 2 P(S’)=. 8 Econ 10/Mgt 10 Stuffler 11
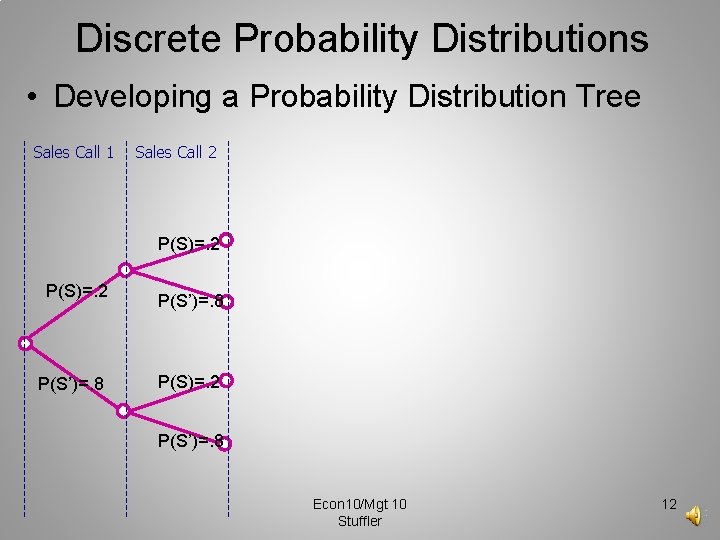
Discrete Probability Distributions • Developing a Probability Distribution Tree Sales Call 1 Sales Call 2 P(S)=. 2 P(S’)=. 8 Econ 10/Mgt 10 Stuffler 12
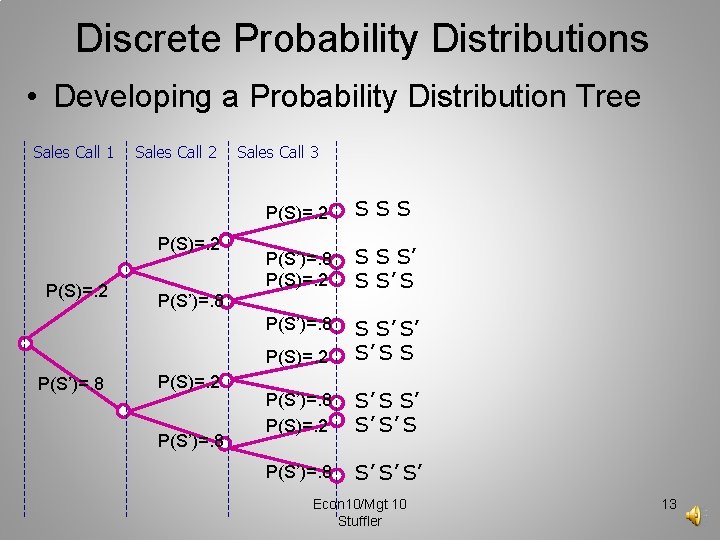
Discrete Probability Distributions • Developing a Probability Distribution Tree Sales Call 1 Sales Call 2 P(S)=. 2 P(S’)=. 8 Sales Call 3 P(S)=. 2 SSS P(S’)=. 8 P(S)=. 2 S S S’ S P(S’)=. 8 P(S)=. 2 S S’ S’ S’ S S P(S’)=. 8 P(S)=. 2 S’ S’ S’ S P(S’)=. 8 S’ S’ S’ P(S’)=. 8 P(S)=. 2 P(S’)=. 8 Econ 10/Mgt 10 Stuffler 13
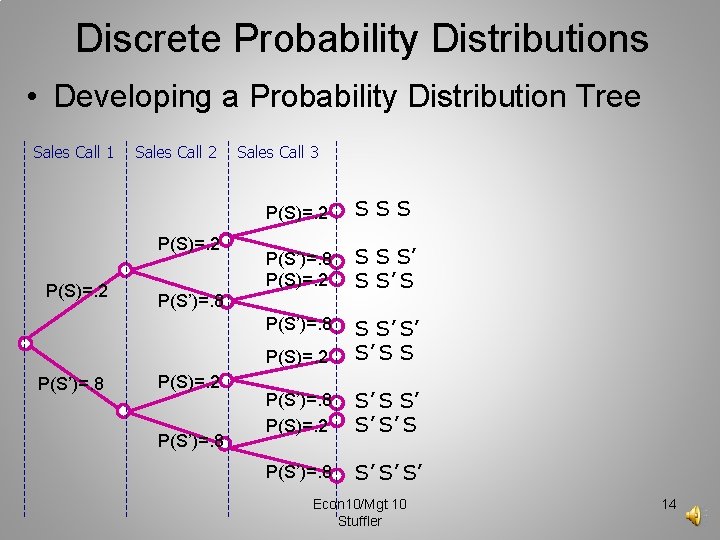
Discrete Probability Distributions • Developing a Probability Distribution Tree Sales Call 1 Sales Call 2 P(S)=. 2 P(S’)=. 8 Sales Call 3 P(S)=. 2 SSS P(S’)=. 8 P(S)=. 2 S S S’ S P(S’)=. 8 P(S)=. 2 S S’ S’ S’ S S P(S’)=. 8 P(S)=. 2 S’ S’ S’ S P(S’)=. 8 S’ S’ S’ P(S’)=. 8 P(S)=. 2 P(S’)=. 8 Econ 10/Mgt 10 Stuffler 14

Discrete Probability Distributions • Developing a Probability Distribution Sales Call 1 Sales Call 2 P(S)=. 2 P(S’)=. 8 Sales Call 3 P(S)=. 2 SSS P(S’)=. 8 P(S)=. 2 S S S’ S P(S’)=. 8 P(S)=. 2 S S’ S’ S’ S S P(S’)=. 8 P(S)=. 2 S’ S’ S’ S P(S’)=. 8 S’ S’ S’ ‘)=. 8 P(S)=. 2 P(S’)=. 8 Econ 10/Mgt 10 Stuffler X 3 2 1 0 P(x). 23 =. 008 3(. 032)=. 096 3(. 128)=. 384. 83 =. 512 15
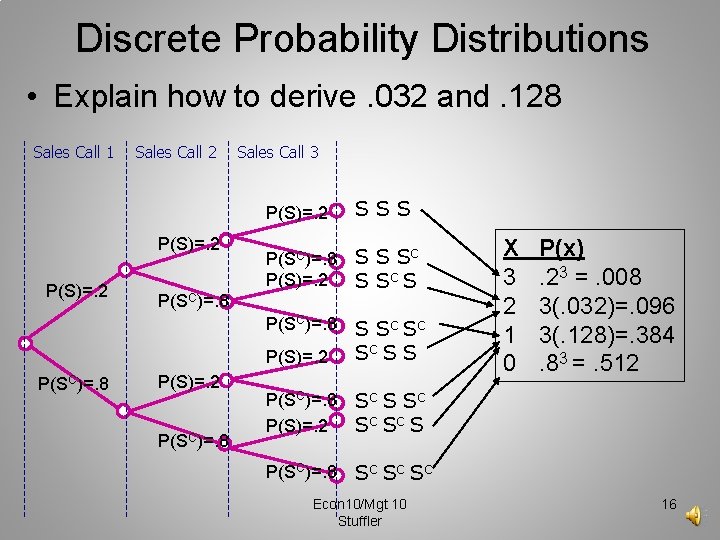
Discrete Probability Distributions • Explain how to derive. 032 and. 128 Sales Call 1 Sales Call 2 P(S)=. 2 P(SC)=. 8 Sales Call 3 P(S)=. 2 SSS P(SC)=. 8 P(S)=. 2 S S SC S P(SC)=. 8 P(S)=. 2 S S C SC SC S S P(SC)=. 8 P(S)=. 2 SC S S C SC SC S P(SC)=. 8 SC SC SC P(SC)=. 8 P(S)=. 2 P(SC)=. 8 Econ 10/Mgt 10 Stuffler X 3 2 1 0 P(x). 23 =. 008 3(. 032)=. 096 3(. 128)=. 384. 83 =. 512 16

Discrete Probability Distributions • The P(X=2) is: Sales Call 1 Sales Call 2 Sales Call 3 (. 2)(. 8)=. 032 P(S)=. 2 P(SC)=. 8 P(S)=. 2 SSS P(SC)=. 8 P(S)=. 2 S S SC S P(SC)=. 8 P(S)=. 2 S S C SC SC S S P(SC)=. 8 P(S)=. 2 SC S S C SC SC S P(SC)=. 8 SC SC SC P(SC)=. 8 P(S)=. 2 P(SC)=. 8 Econ 10/Mgt 10 Stuffler X 3 2 1 0 P(x). 23 =. 008 3(. 032)=. 096 3(. 128)=. 384. 83 =. 512 17

Discrete Probability Distributions A discrete probability distribution represents a population Example: Population of number of TVs per household Example: Population of sales call outcomes Since we have populations, we can describe them by computing various parameters: Population Mean and Population Variance Econ 10/Mgt 10 Stuffler 18

Discrete Probability Distributions Population Mean (Expected Value) - Weighted average of all values with the weights being the probabilities - Expected value of X, E(X) Econ 10/Mgt 10 Stuffler 19

Discrete Probability Distributions Population variance - weighted average of the squared deviations from the mean. “Short cut” formula for the variance Standard deviation formula Econ 10/Mgt 10 Stuffler 20

Discrete Probability Distributions Find the mean, variance, and standard deviation for the population of the number of color televisions per household. = 0(. 012) + 1(. 319) + 2(. 374) + 3(. 191) + 4(. 076) + 5(. 028) = 2. 084 Econ 10/Mgt 10 Stuffler 21

Discrete Probability Distributions Find the mean, variance, and standard deviation for the population of the number of color televisions per household. = (0 – 2. 084)2(. 012) + (1 – 2. 084)2(. 319)+…+(5 – 2. 084)2(. 028) = 1. 107 Econ 10/Mgt 10 Stuffler 22

Discrete Probability Distributions Find the mean, variance, and standard deviation for the population of the number of color televisions per household. = 1. 052 Econ 10/Mgt 10 Stuffler 23

Discrete Probability Distributions Special application of Expected Value Suppose the probability that an insurance agent makes a sale is. 20 and after costs earns a commission of $525. If he/she does not make a sale, they must pay $75 in costs. What is their expected value from a sales call? Does the benefit exceed the cost or is the opposite true? Econ 10/Mgt 10 Stuffler 24

Discrete Probability Distributions Special application of Expected Value Let X be the discrete random variable of making a sale call x Sale $ 525 No Sale - $ 75 P(x). 20. 80 x • P(x) $ 105 - $ 60 E(x) = μ = ∑ x. P(x) = $ 45 Econ 10/Mgt 10 Stuffler 25

Binomial Distribution Binomial distribution is the probability distribution that results from doing a “binomial experiment” which have the properties: 1. 2. 3. 4. Fixed number of identical trials, represented as n. Each trial has two possible outcomes: a “success” or “failure” For all trials, the probability of success, P(success)=p, and the probability of failure, P(failure)=1–p=q, are constant. The trials are independent Econ 10/Mgt 10 Stuffler 26
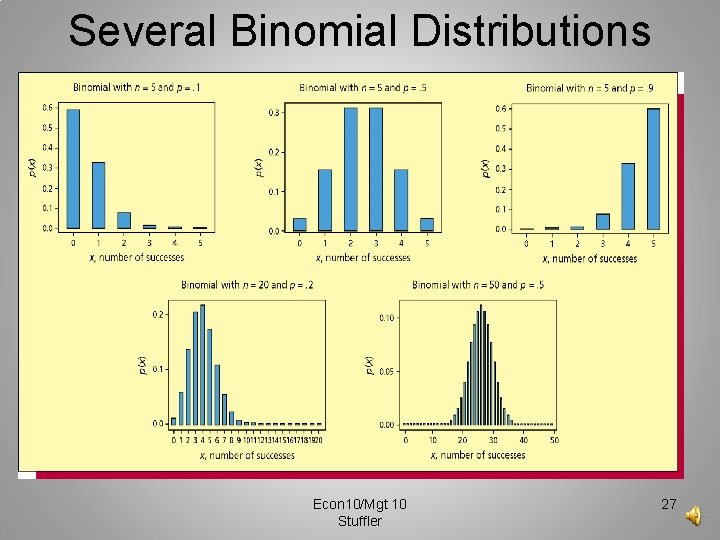
Several Binomial Distributions Econ 10/Mgt 10 Stuffler 27

Binomial Distribution Success and failure: labels for binomial experiment outcomes, no value judgment is implied. EX: Coin flip results in either heads or tails. If we define “heads” as success, then “tails” is considered a failure. Other binomial examples: An election candidate wins or loses An employee is male or female A worker is employed or unemployed Econ 10/Mgt 10 Stuffler 28

Binomial Distribution Binomial Formula: where x = number of successes in n trials, n – x = number of failures in n trials, px = the probability of success raised to the number of successes, and qn-x = probability of failure raised to the number of failures Econ 10/Mgt 10 Stuffler 29

Binomial Distribution The random variable of a binomial experiment is defined as the number of successes in the n trials, and is called the binomial random variable. EX: Flip a fair coin 10 times – 1) Fixed number of trials n=10 – 2) Each trial has two possible outcomes {heads (success), tails (failure)} – 3) P(success)= 0. 50; P(failure)=1– 0. 50 = 0. 50 – 4) The trials are independent (i. e. the outcome of heads on the first flip will have no impact on subsequent coin flips). Flipping a coin ten times is a binomial experiment since all conditions are met. Econ 10/Mgt 10 Stuffler 30

Binomial Distribution Another sales call example: Assume a mutual fund salesman knows that there is 20% chance of closing a sale on each call he makes. We want to determine the probability of making two sales in three calls: P(sale) =. 2 P(no sale) =. 8 P(X=2) = 3! 2!(3 -2)! . 22. 8. 8 =. 096 Econ 10/Mgt 10 Stuffler 31

Binomial Distribution Another sales call example: Assume a mutual fund salesman knows that there is 20% chance of closing a sale on each call he makes We want probability of making two sales in three calls P(sale) =. 2 P(no sale) =. 8 GOOD NEWS! Megastat→Probability→Discrete Distributions→Binomial Econ 10/Mgt 10 Stuffler 32

Binomial Distribution Econ 10/Mgt 10 Stuffler 33

Pat Statsly is a student (not a good student) taking a statistics course. Pat’s exam strategy is to rely on luck for the first test. The test consists of 10 multiple-choice questions. Each question has five possible answers, only one of which is correct. Pat plans to guess the answer to each question. What is the probability that Pat gets no answers correct? What is the probability that Pat gets two answers correct? Econ 10/Mgt 10 Stuffler 34

Pat Statsly n=10 P(correct) = p = 1/5 =. 20 P(wrong) = q =. 80 Is this a binomial experiment? Check the conditions Econ 10/Mgt 10 Stuffler 35

Pat Statsly n=10 P(correct) = p = 1/5 =. 20 P(wrong) = q =. 80 Is this a binomial experiment? Check the conditions: There is a fixed finite number of trials (n=10). An answer can be either correct or incorrect. The probability of a correct answer (P(success)=. 20) does not change from question to question. Each answer is independent of the others. Econ 10/Mgt 10 Stuffler 36

Pat Statsly n=10, and P(success) =. 20 What is the probability that Pat gets no answers correct? EX: P(x=0) What’s the interpretation of this result? Econ 10/Mgt 10 Stuffler 37

Pat Statsly • n=10, and P(success) =. 20 What is the probability that Pat gets no answers correct? EX: P(x=0) Pat has about an 11% chance of getting no answers correct using the guessing strategy. Econ 10/Mgt 10 Stuffler 38

Pat Statsly Econ 10/Mgt 10 Stuffler 39

Pat Statsly n=10, and P(success) =. 20 What is the probability that Pat gets two answers correct? EX: P(x=2) Econ 10/Mgt 10 Stuffler 40

Pat Statsly We have been using the binomial probability distribution to find probabilities for individual values of x. To answer the question: “Find the probability that Pat fails the quiz” requires a cumulative probability, that is, P(X ≤ x) If a grade on the quiz is less than 50% (i. e. 5 questions out of 10), that’s considered a failed quiz. Econ 10/Mgt 10 Stuffler 41

Pat Statsly We have been using the binomial probability distribution to find probabilities for individual values of x. To answer the question: “Find the probability that Pat fails the test” requires a cumulative probability, that is, P(X ≤ x) If a grade on the test is less than 50% (i. e. , 5 questions out of 10), that’s considered a failed test. We want to know what is: P(X ≤ 4) to answer Econ 10/Mgt 10 Stuffler 42

Pat Statsly P(X ≤ 4) = P(0) + P(1) + P(2) + P(3) + P(4) =. 9672 What is the interpretation of this result? Econ 10/Mgt 10 Stuffler 43

Pat Statsly Its about 97% probable that Pat will fail the test using the luck strategy and guessing at answers. Econ 10/Mgt 10 Stuffler 44

Binomial Table Calculating binomial probabilities by hand is tedious and error prone. There is an easier way. Refer to Table E-6 in the Appendices. For the Pat Statsly example, n=10, so go to the n=10 table: Look in the Column, p=. 20 and substitute into: P(X ≤ 4) = P(0) + P(1) + P(2) + P(3) + P(4) P(X ≤ 4) =. 1074 +. 2684 +. 3020 +. 2013 +. 0881 =. 9672 The probability of Pat failing the test is 96. 72% Econ 10/Mgt 10 Stuffler 45

Poisson Distribution Named for Simeon Poisson, Poisson distribution Discrete probability distribution There there are no trials Number of independent events (successes) occurring in a fixed time period or region of space that occur with a known average rate such as, arrivals, departures, or accidents, number of baskets in a quarter, etc. Econ 10/Mgt 10 Stuffler 46

Poisson Distribution For example: • The number of cars arriving at a service station in 1 hour. (The interval of time is 1 hour. ) • The number of flaws in a bolt of cloth. (The specific region is a bolt of cloth. ) • The number of accidents in 1 day on a particular stretch of highway. (The interval is defined by both time, 1 day, and space, the particular stretch of highway. ) Econ 10/Mgt 10 Stuffler 47

Poisson Distribution Poisson random variable - number of successes that occur in a period of time or an interval of space EX: On average, 96 trucks arrive at a border crossing every hour. EX: Number of typographical errors in a new textbook edition averages 1. 5 per 100 pages. Econ 10/Mgt 10 Stuffler 48

Poisson Distribution… The Poisson random variable is the number of successes that occur in a period of time or an interval of space in a Poisson experiment. successes EX: On average, 96 trucks arrive at a border crossing every hour. time period E. g. The number of typographic errors in a new textbook edition averages 1. 5 per 100 pages. successes (? !) interval Econ 10/Mgt 10 Stuffler 49

Poisson Distribution Poisson experiment has four defining characteristics or properties: 1. The number of successes that occur in any interval is independent of the number of successes that occur in any other interval 2. The probability of a success in an interval is the same for all equal-size intervals 3. The probability of a success is proportional to the size of the interval 4. Only one value is required to determine the probability of a designated number of events occurring during an interval Econ 10/Mgt 10 Stuffler 50

Poisson Distribution The probability that a Poisson random variable assumes a value of x is given by: µ = n(p) = number of successes times the probability of success The unit of time or the interval should be short enough so that the mean rate is not large (µ < 20) YOUR TEXTBOOK USES λ (lambda) REPRESENT THE MEAN NUMBER OF SUCCESSES IN THE INTERVAL Econ 10/Mgt 10 Stuffler 51

Poisson Distribution EXAMPLE The number of typographical errors in new editions of textbooks varies considerably from book to book. After some analysis she concludes that the number of errors is Poisson distributed with a mean of 1. 5 per 100 pages. The instructor randomly selects 100 pages of a new book. What is the probability that there are no typos? MEGASTAT→PROBABILITY→DISCRETE DISTRIBUTIONS→POISSON AND ENTER THE MEAN VALUE: 1. 5, CLICK OK Econ 10/Mgt 10 Stuffler 52

Poisson Distribution Econ 10/Mgt 10 Stuffler 53

Mean and Variance of a Poisson Random Variable If x is a Poisson random variable with parameter , then Mean number of events per unit of time or space = µ Variance = V(X) = σ2 = μ Econ 10/Mgt 10 Stuffler 54

Poisson Distribution As mentioned on the first Poisson Distribution slide: The probability of a success is proportional to the size of the interval Thus, knowing an error rate of 1. 5 typos per 100 pages, we can determine a mean value for a 400 page book as: μ = n(p) = 1. 5(4) = 6 typos / 400 pages. Econ 10/Mgt 10 Stuffler 55

Poisson Distribution For a 400 page book, what is the probability that there are no typos? P(X=0) = Interpretation? Econ 10/Mgt 10 Stuffler 56

GOOD NEWS! Go to Excel, Megastat, Probability, Discrete, Poisson. Type in the mean, μ, 6, then OK. For a mean of 6, the Excel result is 0. 00248 Econ 10/Mgt 10 Stuffler 57

Poisson Distribution For a 400 page book, what is the probability that there are five or less typos? P(X≤ 5) = P(0) + P(1) + … + P(5) Another alternative is to refer to Table E-7 in the Appendices For x = 5, μ =6, and P(X ≤ 5) = P(0) + … + P(5) =. 4456 There is about a 45% chance that there will be 5 or less typos Econ 10/Mgt 10 Stuffler 58

Hypergeometric Distribution If a sample is taken from a finite population without replacement, the probability of X number of successes, follows the hypergeometric distribution. NOTE: When you see “without replacement, ” this indicates that hypergeometric trials are dependent. Econ 10/Mgt 10 Stuffler 59

Hypergeometric Distribution For both the Binomial Distribution and the Hypergeometric Distribution, there are two possible outcomes for the random discrete variable: Success or Failure Econ 10/Mgt 10 Stuffler 60

Hypergeometric Distribution The difference is that for Hypergeometric each trial is “without replacement, ” so the probability changes from one draw to the next For Binomial, the probability of success and failure remain constant since each trial or draw is independent Econ 10/Mgt 10 Stuffler 61

Hypergeometric Distribution 1. 2. 3. 4. Trials are NOT independent Finite population Sample without replacement Probability of success and failure changes from trial to trial Econ 10/Mgt 10 Stuffler 62

Hypergeometric Distribution r P(x) = x N–r n–x N n μ=nr N σ2 = r (N-r) n (N-n) N 2 (N-1) where N = Total number in the population n = number in the sample, x = number selected or drawn, r = number of successes in N Econ 10/Mgt 10 Stuffler 63

Hypergeometric Distribution EXAMPLE: Assume that 3 stocks are chosen randomly from a list of 10 stocks and that of the 10 stocks 4 stocks pay dividends. The number (x) of the three selected stocks that pay a dividend is a hypergeometric random variable. Econ 10/Mgt 10 Stuffler 64

Hypergeometric Distribution N=10, n=3, r = 4 and x = number of the 3 stocks selected that pay a dividend Calculate the mean, the variance and the probability that none of the 3 stocks pay dividends? Econ 10/Mgt 10 Stuffler 65

Hypergeometric Distribution 4 10 – 4 4! 6! P(0) = 0 3 -0 = 0!(4 -0)! 3!(6 -3)! = 1 10 10! 6 3 3!(10 -3)! μ = (3)(4) = 1. 2 10 σ2 = 4(10 -4)3(10 -3) =. 56, σ =. 75 (10)2 (10 -1) Econ 10/Mgt 10 Stuffler 66

Hypergeometric Distribution GOOD NEWS! Go to Excel→Megastat→Probability →Discrete Probability Distributions →Hypergeometric, enter the required data Econ 10/Mgt 10 Stuffler 67

Hypergeometric Distribution Econ 10/Mgt 10 Stuffler 68

Discrete Probability WHICH DISTRIBUTION? Sony issued a recall for their plasma screen TVs. They choose 25 TVs and 7 do not operate. If the inspector chooses 3 at random from the 25, what is the probability that 2 of the 3 do not operate? Econ 10/Mgt 10 Stuffler 69

Discrete Probability WHICH DISTRIBUTION? When Wet Water drills a well, their success rate is. 55 and their profit is $2, 550. If they do not find water, they lose $1, 500. Econ 10/Mgt 10 Stuffler 70

Discrete Probability WHICH DISTRIBUTION? The US unemployment rate is calculated from survey data of 60, 000 households. What is the probability that no more than 5, 000 respondents are unemployed? Econ 10/Mgt 10 Stuffler 71

Discrete Probability WHICH DISTRIBUTION? US Transportation and Safety Board reports the annual average number of plane crashes is 14. 6. For a given month, what is the probability that at 2 crashes will occur? That 3 crashes will occur? Econ 10/Mgt 10 Stuffler 72

Discrete Probability WHICH DISTRIBUTION? The US Statistical Abstract of the US tracks many data items such as, the average number of automobiles per household. The average for 2009 is 2. 5 autos. What is the probability that the 2010 average is at least 3 autos? Econ 10/Mgt 10 Stuffler 73

Discrete Random Variables Summary: Two Types of Random Variables Discrete Probability Distributions The Binomial Distribution The Poisson Distribution The Hypergeometric Distribution Econ 10/Mgt 10 Stuffler 74
- Slides: 74