Prezov charakteristiky statick sted soustavy sil tit Geometrick

Průřezové charakteristiky, statický střed soustavy sil, těžiště. • Geometrické útvary (čáry, obrazce) nahradíme fiktivními rovnoběžnými silami působícími v těžištích jednotlivých částí – u čáry je to délka úseček d, u obrazce plocha A. Těžiště je statickým středem soustavy těchto rovnoběžných sil. x. T x z 1 1 z. T F 1= A 1 z 2 = z 3 F 1 = A 1 T Acel= A 1+A 2 - A 3 Acel F 3 = A 3 3 Sx = A 1. z 1 + A 2. z 2 - A 3. z 3 Sx = Acel. z. T 2 F 2 = A 2 z otvor analogicky x. T

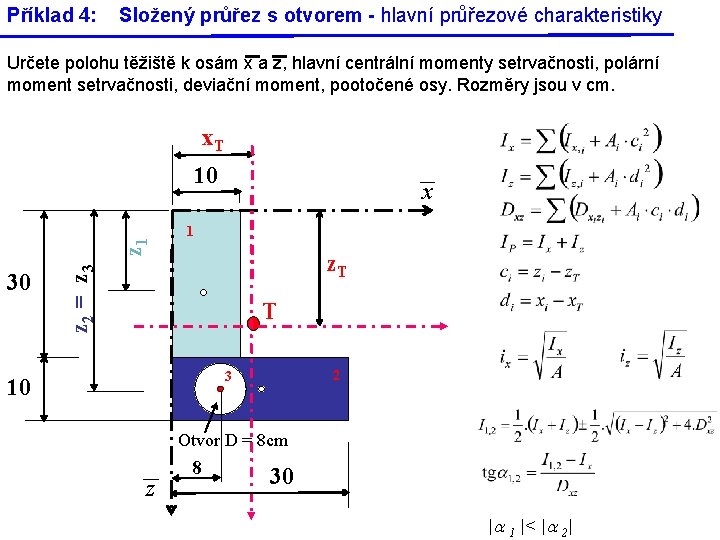
Příklad 4: Složený průřez s otvorem - hlavní průřezové charakteristiky Určete polohu těžiště k osám x a z, hlavní centrální momenty setrvačnosti, polární moment setrvačnosti, deviační moment, pootočené osy. Rozměry jsou v cm. x. T 30 x 1 z. T z 2 = z 3 z 1 10 T 2 3 10 Otvor D = 8 cm z 8 30 |a 1 |< |a 2|

Příklad 1: Těžiště lomené čáry Stanovte polohu těžiště lomené čáry, která je dána spojnicí bodů: A(-5; -6), B(0; 0), C(0; 3), D(6; 6). 1 x Postup: 1. 2. 3. 4. 5. 6. délky jednotlivých úseček (di) celková délka ( d = ∑ di ) souřadnice dílčích těžišť statický moment k ose x: Sx = ∑di. z. T, i statický moment k ose z: Sz = ∑di. x. T, i souřadnice těžiště lomené čáry: Sx = d. z. T → z. T = Sx / d Sz = d. x. T → x. T = Sz / d 2 z 3 Výsledky: 1. d 1 = 7, 81 m, d 2 = 3 m, d 3 = 6, 71 m 2. d = ∑ di = 17, 52 m 3. T 1[-2, 5; -3], T 2[0; 1. 5], T 3[3; 4, 5] 4. Sx = ∑di. z. T, i = 11, 27 m 2 5. Sz = ∑di. x. T, i = 0, 605 m 2 6. souřadnice těžiště lomené čáry: z. T = Sx / d = 0, 64 m x. T = Sz / d = 0, 03 m 1. T [0, 03; 0, 64]

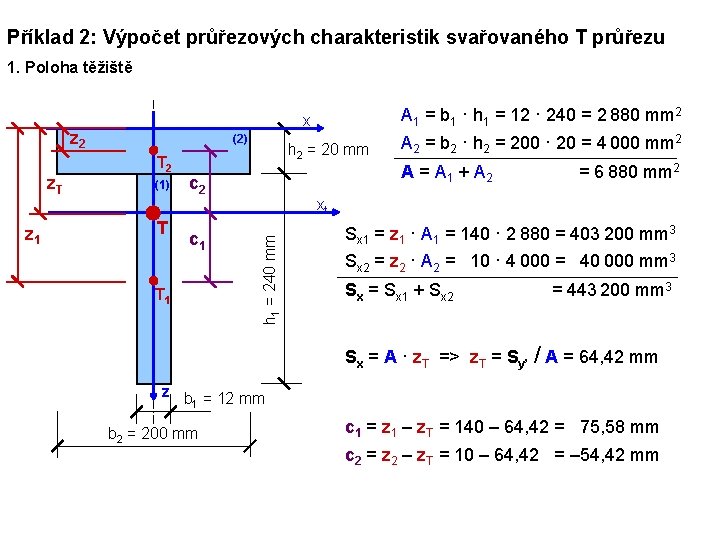
Příklad 2: Výpočet průřezových charakteristik svařovaného T průřezu 1. Poloha těžiště z 2 z 1 (2) T 2 (1) T h 2 = 20 mm c 2 c 1 T 1 A 2 = b 2 · h 2 = 200 · 20 = 4 000 mm 2 A = A 1 + A 2 = 6 880 mm 2 xt h 1 = 240 mm z. T A 1 = b 1 · h 1 = 12 · 240 = 2 880 mm 2 x Sx 1 = z 1 · A 1 = 140 · 2 880 = 403 200 mm 3 Sx 2 = z 2 · A 2 = 10 · 4 000 = 40 000 mm 3 Sx = Sx 1 + Sx 2 = 443 200 mm 3 Sx = A · z. T => z. T = Sy’ / A = 64, 42 mm z b = 12 mm 1 b 2 = 200 mm c 1 = z 1 – z. T = 140 – 64, 42 = 75, 58 mm c 2 = z 2 – z. T = 10 – 64, 42 = – 54, 42 mm

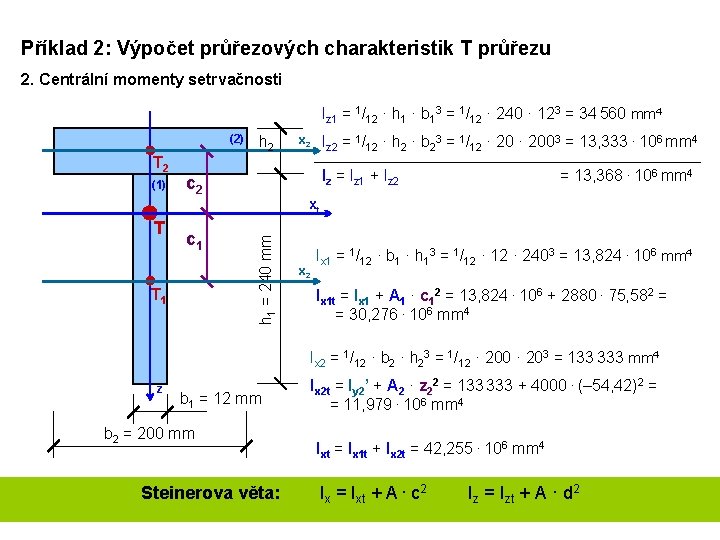
Příklad 2: Výpočet průřezových charakteristik T průřezu 2. Centrální momenty setrvačnosti Iz 1 = 1/12 · h 1 · b 13 = 1/12 · 240 · 123 = 34 560 mm 4 (2) T 2 (1) h 2 Iz 2 = 1/12 · h 2 · b 23 = 1/12 · 2003 = 13, 333 · 106 mm 4 x 2 Iz = Iz 1 + Iz 2 c 2 = 13, 368 · 106 mm 4 T c 1 T 1 h 1 = 240 mm xt x 2 Ix 1 = 1/12 · b 1 · h 13 = 1/12 · 2403 = 13, 824 · 106 mm 4 Ix 1 t = Ix 1 + A 1 · c 12 = 13, 824 · 106 + 2880 · 75, 582 = = 30, 276 · 106 mm 4 Ix 2 = 1/12 · b 2 · h 23 = 1/12 · 200 · 203 = 133 333 mm 4 z b 1 = 12 mm b 2 = 200 mm Steinerova věta: Ix 2 t = Iy 2’ + A 2 · z 22 = 133 333 + 4000 · (– 54, 42)2 = = 11, 979 · 106 mm 4 Ixt = Ix 1 t + Ix 2 t = 42, 255 · 106 mm 4 Ix = Ixt + A · c 2 Iz = Izt + A · d 2

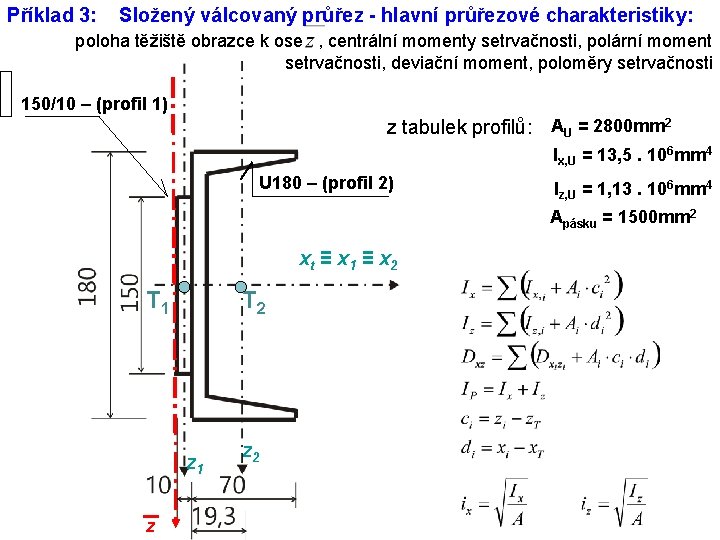
Příklad 3: Složený válcovaný průřez - hlavní průřezové charakteristiky: poloha těžiště obrazce k ose , centrální momenty setrvačnosti, polární moment setrvačnosti, deviační moment, poloměry setrvačnosti 150/10 – (profil 1) z tabulek profilů: AU = 2800 mm 2 Ix, U = 13, 5. 106 mm 4 U 180 – (profil 2) Iz, U = 1, 13. 106 mm 4 Apásku = 1500 mm 2 xt ≡ x 1 ≡ x 2 T 1 T 2 z 1 z z 2

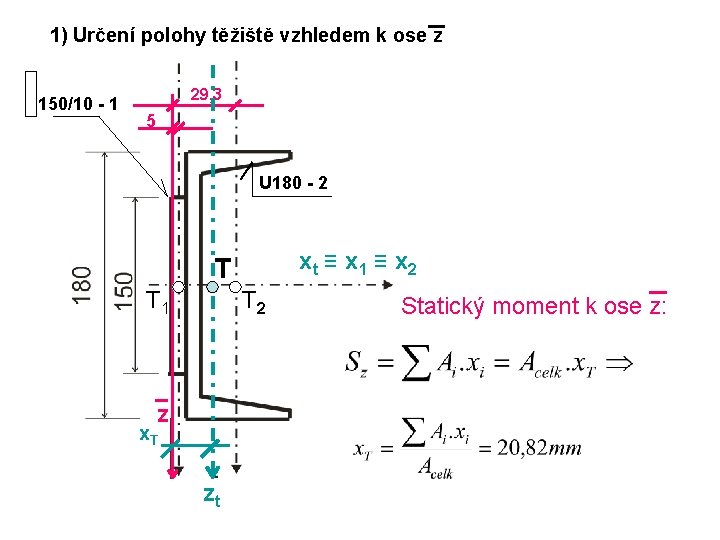
1) Určení polohy těžiště vzhledem k ose z 150/10 - 1 29, 3 5 U 180 - 2 xt ≡ x 1 ≡ x 2 T T 1 T 2 z x. T zt Statický moment k ose z:

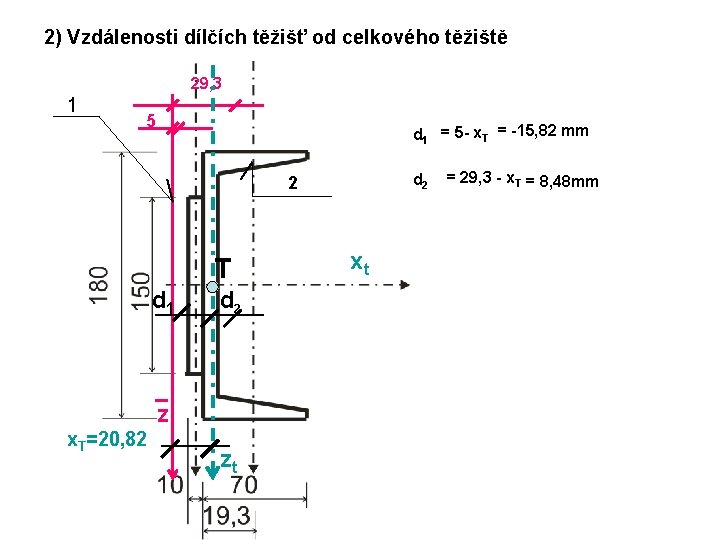
2) Vzdálenosti dílčích těžišť od celkového těžiště 29, 3 1 5 d 1 = 5 - x. T = -15, 82 mm d 2 2 T d 1 d 2 z x. T=20, 82 zt xt = 29, 3 - x. T = 8, 48 mm

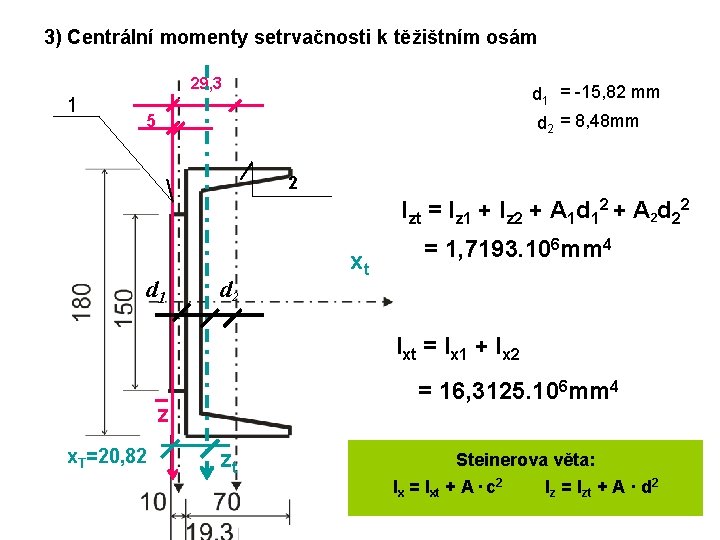
3) Centrální momenty setrvačnosti k těžištním osám 29, 3 1 d 1 = -15, 82 mm d 2 = 8, 48 mm 5 2 Izt = Iz 1 + Iz 2 + A 1 d 12 + A 2 d 22 d 1 d 2 xt = 1, 7193. 106 mm 4 Ixt = Ix 1 + Ix 2 = 16, 3125. 106 mm 4 z x. T=20, 82 zt Steinerova věta: Ix = Ixt + A · c 2 Iz = Izt + A · d 2

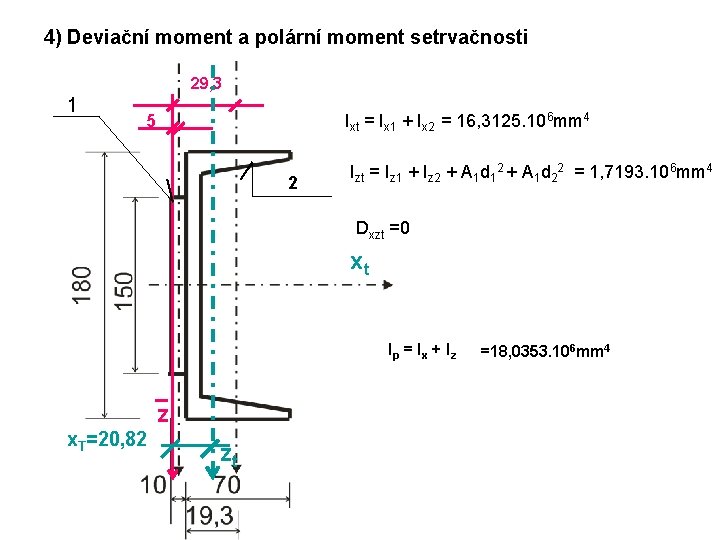
4) Deviační moment a polární moment setrvačnosti 29, 3 1 5 Ixt = Ix 1 + Ix 2 = 16, 3125. 106 mm 4 2 Izt = Iz 1 + Iz 2 + A 1 d 12 + A 1 d 22 = 1, 7193. 106 mm 4 Dxzt =0 xt Ip = I x + I z z x. T=20, 82 zt =18, 0353. 106 mm 4

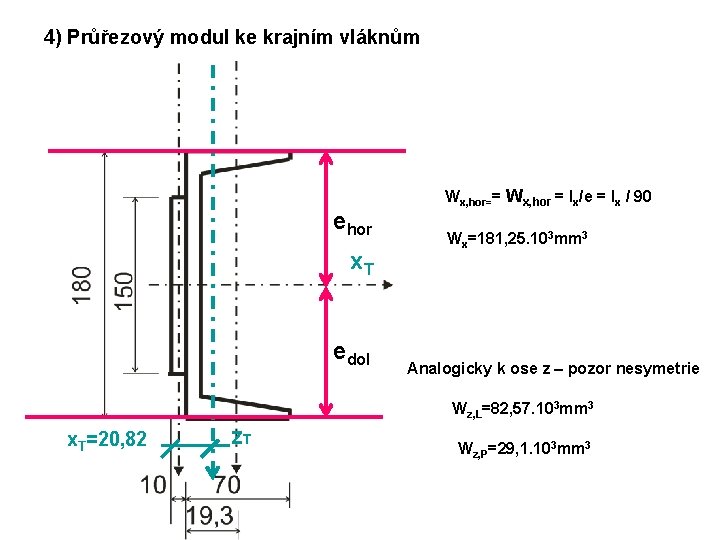
4) Průřezový modul ke krajním vláknům ehor x. T edol Wx, hor== Wx, hor = Ix/e = Ix / 90 Wx=181, 25. 103 mm 3 Analogicky k ose z – pozor nesymetrie Wz, L=82, 57. 103 mm 3 x. T=20, 82 z. T Wz, P=29, 1. 103 mm 3