Predicate Logic Translation Gregory Chapter 5 3 5

Predicate Logic Translation Gregory Chapter 5. 3 – 5. 4

Contents • Simple Symbolization in the language P - Satisfaction and Truth in P - Non-Categorical Claims ・ Quantifier-Negation Equivalences - Categorical Propositions ・ Quantifiers and Connectives • Complex Symbolization in P - Overlapping Quantifiers - The Identity Predicate - Definite Descriptions: Russell’s Theory of Descriptions

5. 3 Simple Symbolization

Satisfaction and Truth in P (Informal) It is important to have at least a rough understanding of quantificational semantics before proceeding to translate English into P. Consider the following rough definitions:

5. 3. 1 Non-Categorical Claims UD: {animals – human or other, real or mythological} Predicates: L: __ is a logician; P: __ is a programmer; U: __ is a unicorn; O: __is onehorned; F: __is a friend of__ Individual Constants: a: Ada Lovelace; b: Charles Babbage; c: Lewis Carroll • Singular Statements - Ada is a programmer Pa - Babbage is not a programmer. ¬ Pb - Babbage is Ada’s friend. Fba - Babbage is not Lewis Carroll’s friend ¬ Fbc

5. 3. 1 Non-Categorical Claims UD: {animals – human or other, real or mythological} Predicates: L: __ is a logician; P: __is a programmer; U: __is a unicorn; O: __is onehorned; F: __is a friend of__ Individual Constants: a: Ada Lovelace; b: Charles Babbage; c: Lewis Carroll Existence and Non-Existence - There are no unicorns. ¬ (∃x)Ux or (∀x) ¬ Ux ・ It is not the case that there exists an x such that x is a unicorn ・ For all x, x is not a unicorn. - There are logicians. (∃x)Lx or ¬ (∀x) ¬ Lx ・ There exists an x such that x is a logician. ・ It is not the case that all x are not logician.

Quantifier-Negation (‘Push-Through’) Rules • Predicates: M: __is material; P: __is perfect - Nothing is perfect. ¬ (∃x)Px or (∀x) ¬ Px - Not everything is material. ¬ (∀x) Mx or (∃x) ¬ Mx • Note: the second two equivalence are unnecessary since we can push through the negation and then elimination double negation.

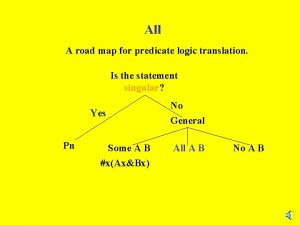
5. 3. 1 Aristotelian Categorical Propositions UD: {animals – human or other, real of mythological} Predicates: L: __ is a logician; P: is a programmer; U: is a unicorn; O: is one-horned; F: __is a friend of__ Individual Constants: a: Ada Lovelace; b: Charles Babbage; c: Lewis Carroll • All unicorns are one-horned. (∀x)(Ux → Ox) • No logicians are one-horned. ¬ (∃x)(Lx ∧ Ox) • Some logicians are programmers. (∃x)(Lx ∧ Px) • Some logicians are not programmers. (∃x)(Lx ∧ ¬ Px)

5. 4. 3 Categorical Claims • We’ll assume the ‘Modern’ Square of Opposition as above in translating categorical sentences. • Note: the most counterintuitive feature is that ‘All S are P’ doesn’t imply ‘Some S are P’ because we construe ‘All S are P’ as a conditional: for all x, IF x is S then it’s P, which doesn’t commit us to the existence of anything that’s S

Why? • Why do we do this? Why prefer translations according to the Modern Square of Opposition? • Because we want minimalist interpretations. If we want to say more we can add more. - ‘All S are P presupposes but does not assert that there are Ss so we can’t infer that some S are P. - ‘No S are P presupposes but does not assert that there are Ss so we cant infer that some S are not P. ・ No unicorns are vegetarians ・ We can’t infer that some unicorns are not vegetarians because there are no unicorns vegetarian or not: no unicorns are vegetarians because ther are no unicorns!

Ex 5. 3. 2 Quantifiers and Connectives

Ex 5. 3. 2 Quantifiers and Connectives 1. Felix is grey and has whiskers 1. Gf ∧ Wf 2. If Felix is bigger than Sylvester, then Felix is a better 2. Bfs → Mfs mouser than Sylvester. 9. All cats either meow or have whiskers. 9. (∀x)(Mx ∨ Wx) 10. Either all cats meow or all cats have whiskers. 10. (∀x)Mx ∨ (∀x)Wx 17. Some cats like Felix, but not all do. 17. (∃x)Lxf ∧ ¬ (∀y)Lyf 18. Every cat likes itself. 18. (∀x)Lxx 19. If every cat likes itself, then there is a cat that likes 19. (∀x)Lxx → (∃x)Lxf Felix.

5. 3. 4 Exercises 1. Everyone is an accountant. (∀x) Ax 2. Everyone likes Kate. (∀x)Lxk 3. All the accountants are diligent. (∀x)(Ax → Dx) 4. No accountants are diligent. 5. Some accountants are not diligent. 30. If Fred works for Kate, then anyone who works for Fred works for Kate. 31. All and only those who work for Kate like her. 32. Everyone is s. t. that they like Kate if and only iff they work for her. ¬ (∃x)(Ax ∧ Dx), (∀x)(Ax → ¬ Dx) (∃x)(Ax ∧ ¬ Dx), ¬ (∀x)(Ax → Dx) Wfk → [(∀x)Wxf → Wxk] (∀x)[(Wxk → Lxk) ∧ (Lxk → Wxk)] (∀x)(Lxk ↔ Wxk)

5. 4 Complex Symbolizations Translation involving Overlapping Quantifiers

Overlapping Quantifiers • Somebody loves somebody. • Everybody loves everybody. (∃x)(∃y)Lxy (∀x)(∀y)Lxy • Everybody loves somebody or other. (∀x)(∃y)Lxy • There’s somebody who loves everybody. (∃x)(∀y)Lxy

Somebodies who love everybody

More Love…and Being Loved

Overlapping Quantifier Translation • Where both of the quantifiers are the same no problem. • If different, take care: - Everybody loves somebody (or other): (∀x)(∃y)Lxy We’re talking about everybody—saying that everyone of them is such that there’s someone or other they love. - Somebody loves everybody: (∃x)(∀y)Lxy We’re saying that there’s at least one individual, we don’t know who (but probably a dog), who loves everyone. • Be careful also about order: loving isn’t the same as being loved - Everybody loves somebody ≠ somebody loves everybody (∀x)(∃y)Lxy ≠ (∀x)(∃y)Lyx For all x there’s a y that x loves ≠ Everyone is such that there’s someone who loves them.

5. 4. 2 Exercises 1. Everyone loves everyone. (∀x)(∀y)Lxy 2. Someone loves someone. (∃x)(∃y)Lxy 3. Everyone loves someone. (∀x)(∃y)Lxy 4. Everyone is loved by someone. (∀x)(∃y)Lyx 5. Someone loves everyone. (∃x)(∀y)Lxy 6. Someone is loved by everyone. (∃x)(∀y)Lyx 7. Someone is loved by no one. (∃x)(∀y) ¬ Lyx 8. NOT there’s someone who loves no one. ¬ (∃x)(∀y) ¬ Lxy or (∀x)(∃y)Lxy 9. There’s someone who doesn’t love anyone. (∃x)(∀y) ¬ Lxy 10. Nobody loves everybody. ¬ (∃x)(∀y)Lxy

5. 4. 3 Identity • By identity we mean numerical identity—that what appear to be distinct objects are actually one and the same thing. Object x is identical to object y iff x is y. - Type/Token Ambiguity: distinguish identity from qualitative similarity - Counting by type and by token: individual inscriptions and ‘letters of the alphabet’: how many letters in ‘banana’? • Identity (‘=‘) as a special predicate - Syntactic convention: instead of ‘=xy’ we write ‘x = y’ - Identity is an equivalence relation ・ Reflexive: x = x ・ Symmetric: if x = y then y = x ・ Transitive: if x = y and y = z then x = z - Identity is an indiscernibility relation for all properties: if x = y then x is F if and only if y is F, for all properties F

Identity as the Counting Relation

5. 4. 4 Exercises 1. There at least two cashiers. 2. There at least two cashiers working for Kate. 3. There is exactly one cashier. 4. There is exactly one cashier working for Kate. 5. There is exactly one upbeat cashier working for Kate.

5. 4. 4 Exercises 6. There is exactly one upbeat cashier and he works for Kate. 7. There are exactly two accountants. 8. Exactly two accountants work for Kate. 9. Everyone but Fred works for Kate 10. The cashier is lazy.

Definite Descriptions • A definite description is an expression of the form ‘The so-and-so’, e. g. ‘the cat on the mat’, ‘the 2020 Democratic presidential nominee’, ‘the present king of France’ • From the perspective of surface grammar these are referring expressions, which may figure as the subjects of sentences but… • What if nothing satisfies the description? What are we talking about? How can anything make sense if we aren’t talking about anything? • France is a republic: there is no present King of France!

Why Definite Descriptions are a Problem …or a present King of France!

Definite Descriptions • Solution: Russell’s Theory of Descriptions. • ‘Surface grammar’ is misleading: definite descriptions aren’t names. • Translate in terms of logical machinery: ‘The present King of France is bald’ is existential and general! And false!

Translations: Identity • There is at least one solution. (∃x)Sx • There are no unicorns. ¬ (∃x)Ux • There is more than one prime number. (∃x)Px ∧ (∃y)(Py ∧ y ≠ x) • The present King of France is bald (∃x)[(Kx ∧ (∀y)(Ky → y = x) ∧ Bx]

Why is there a problem about the King of France Excluded Middle: P or not P • Consider the sentence P: ‘The present king of France is bald. ’ • P can’t be true since there is no present king of France. • Since it’s not true it must be false • Therefore we conclude that the present King of France is not bald, i. e. not P • But that’s also false since there is no present king of France • But this seems to violate Excluded Middle since we deny both P and not P

Russell’s solution • ‘The current King of France is bald says that: - (∃x)((Kx ∧ (Kx → (∀y)y = x)) ∧ Bx) • But this is false because the first conjunct it is: here is no current king of France; ‘Kx’ is just plain false. • So the whole thing is just plain false! • It is false (on this account) that the present King of France is bald! - or non-bald - or anything else! • Moral of the Story: Predicate logic gives us a way of translating that licenses inferences but we have to be careful!

The End