PCE STAMP What is the EQUATION of MOTION










- Slides: 16

PCE STAMP What is the EQUATION of MOTION of a QUANTUM VORTEX? Physics & Astronomy UBC Vancouver Pacific Institute for Theoretical Physics

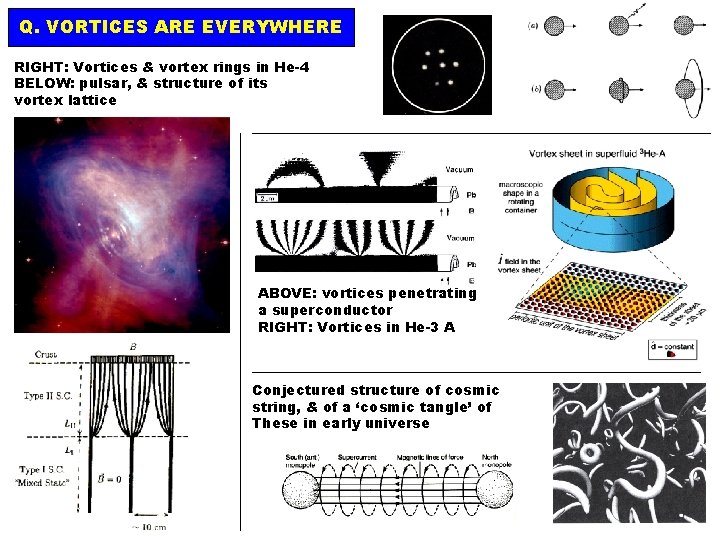
Q. VORTICES ARE EVERYWHERE RIGHT: Vortices & vortex rings in He-4 BELOW: pulsar, & structure of its vortex lattice ABOVE: vortices penetrating a superconductor RIGHT: Vortices in He-3 A Conjectured structure of cosmic string, & of a ‘cosmic tangle’ of These in early universe

FORCES on a QUANTUM VORTEX For the last 40 years there has been a very strenuous debate going on about the form of the equation of motion for a quantum vortex, focusing in particular on (i) what are the dissipative forces acting on it (ii) what is its effective mass Quite incredibly, the fundamental question of quantum vortex dynamics is still highly controversial The discussion is typically framed in terms of the forces acting on a vortex; the following terms are discussed: Magnus force: Iordanskii force: Drag force: = Arises from Berry phase Transverse force from quasiparticles scattering off vortex Longitudinal force from quasiparticles scattering off vortex

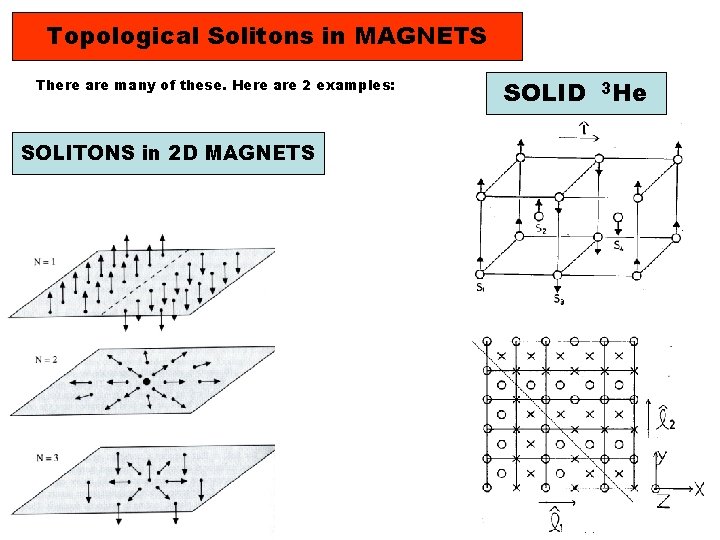
Topological Solitons in MAGNETS There are many of these. Here are 2 examples: SOLITONS in 2 D MAGNETS SOLID 3 He

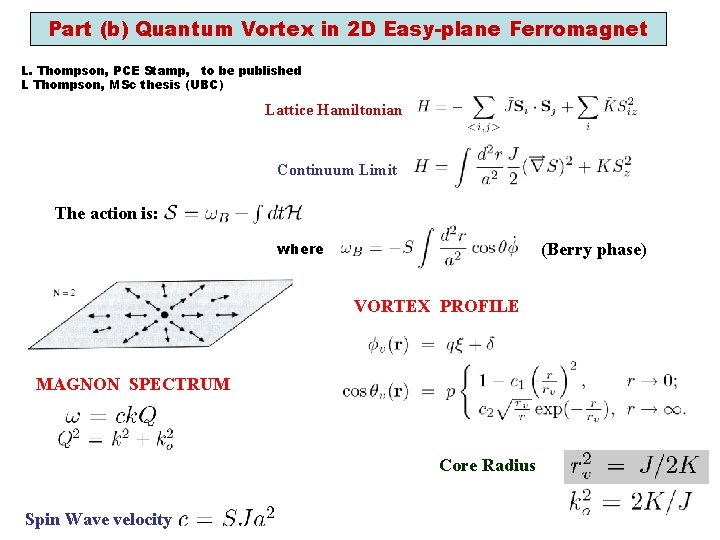
Part (b) Quantum Vortex in 2 D Easy-plane Ferromagnet L. Thompson, PCE Stamp, to be published L Thompson, MSc thesis (UBC) Lattice Hamiltonian Continuum Limit The action is: where (Berry phase) VORTEX PROFILE MAGNON SPECTRUM Core Radius Spin Wave velocity

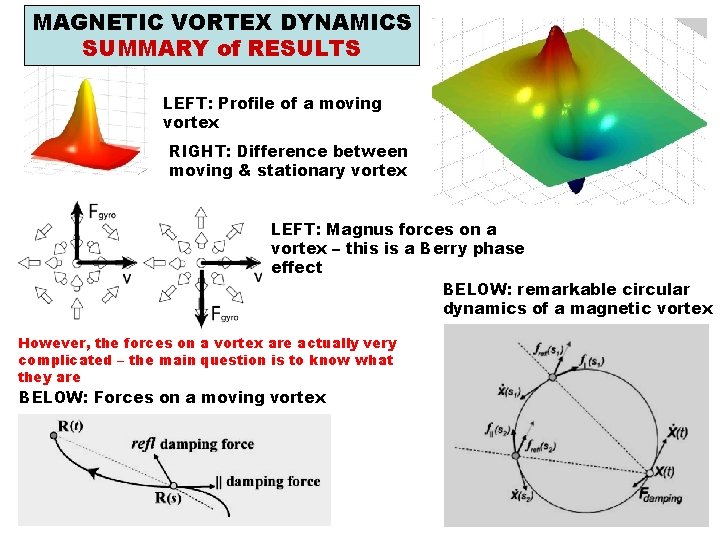
MAGNETIC VORTEX DYNAMICS SUMMARY of RESULTS LEFT: Profile of a moving vortex RIGHT: Difference between moving & stationary vortex LEFT: Magnus forces on a vortex – this is a Berry phase effect BELOW: remarkable circular dynamics of a magnetic vortex However, the forces on a vortex are actually very complicated – the main question is to know what they are BELOW: Forces on a moving vortex

Dynamics OF THE MAGNETIC QUANTUM VORTEX (1) MAGNUS FORCE TERM From the Berry phase one immediately recovers the gyrotropic “Magnus” force: (2) PATH INTEGRAL FORMULATION – VELOCITY EXPANSION Recall that we can always formulate the dynamics for the reduced density matrix as Density matrix propagator where However we are NOT now going to do the usual Caldeira-Leggett trick of assuming a coupling between vortex and magnons which is linear in the magnon variables. As mentioned above, this is not even true for a soliton coupled to its environment. What we need is another expansion parameter, and there is one – if the vortex moves slowly we can expand the coupling in powers of the VORTEX VELOCITY. If we do this we get a result for the effective Lagrangian of the system, given by which we can now use to derive an influence functional Lagrangian for Moving Vortex Lagrangian for magnons coupled to static soliton Linear velocity coupling between magnons and vortex

INFLUENCE FUNCTIONAL From the Lagrangian one finds an influence functional of form: Effective coupling Effective bath propagator: PHASE TERM Now we can always write the influence functional in the form We begin with the phase term – then we can derive equations of motion for the 2 coupled paths, which are best written in the variables Then, in addition to the Magnus force, we find another force acting on the vortex, given by where with frictional terms The definition of the reflection direction is shown – we reflect the velocity vector at time t about the vector connecting the present position with the earlier position. Thus the force contains a memory of the previous path traced by the vortex

DECOHERENCE FUNCTIONAL We also have an imaginary term in the influence functional which can be thought of as supplying a ‘quantum noise’ term in the coupled dynamics of the 2 paths. This gives a “quantum noise” term on the right hand-side of a Quantum Langevin equat However the noise is not only non-Markovian (highly coloured in fact) but also non-local. Thus the real dynamics of a vortex, magnetic or otherwise, has both reactive and dissipative terms that are more complex than those that have been discussed so far. There is definitely a transverse dissipative force having the symmetry of the Iordanskii term, but it is now part of a more complicate time-varying term with memory whose size and form depends on the previous path of the vortex CONCLUSIONS for Dynamics of a SINGLE MAGNETIC VORTEX (1) There is no reason whatsoever to exclude transverse dissipative forces. In fact (2) they are much more complex than previously understood (3) (2) The equations of motion for an assembly of vortices involve all sorts of forces (4) (non-local in time and space) that have not previously been studied.

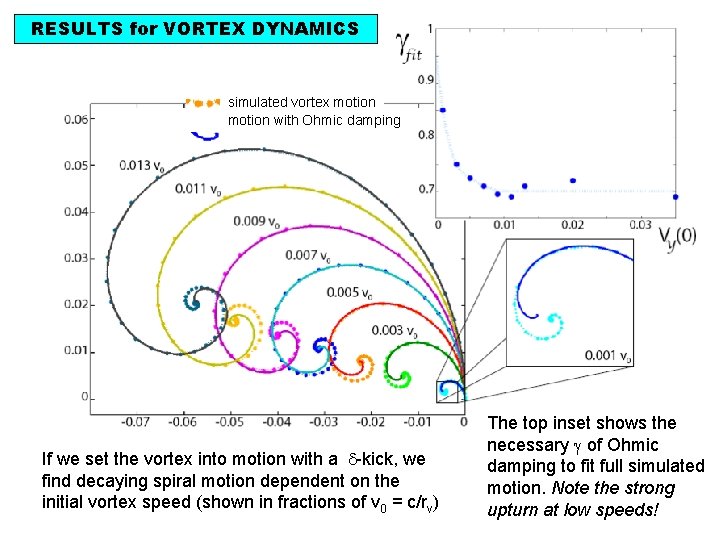
RESULTS for VORTEX DYNAMICS simulated vortex motion with Ohmic damping If we set the vortex into motion with a -kick, we find decaying spiral motion dependent on the initial vortex speed (shown in fractions of v 0 = c/rv) The top inset shows the necessary of Ohmic damping to fit full simulated motion. Note the strong upturn at low speeds!

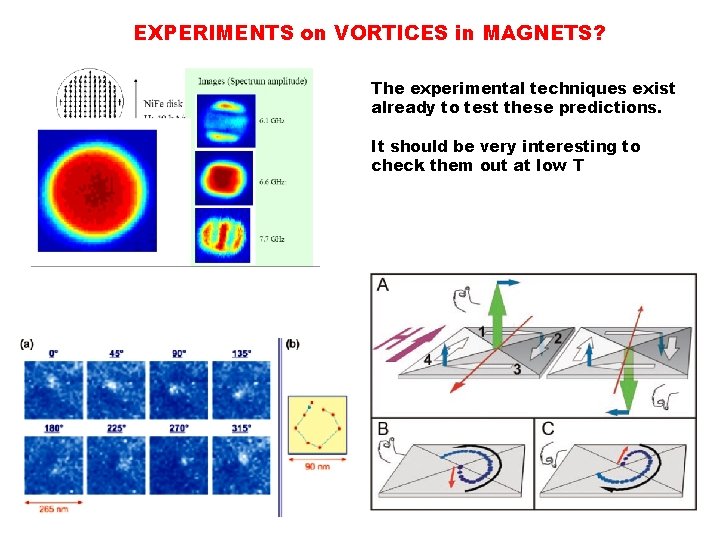
EXPERIMENTS on VORTICES in MAGNETS? The experimental techniques exist already to test these predictions. It should be very interesting to check them out at low T

VORTICES IN A BOSE SUPERFLUID Let’s assume a somewhat simplified model Bose superfluid, with the action Where we define a small fluctuation field by and a vortex field by Where the ‘bare’ vortex field is We now separate off the vortex from the fluctuations; define Then we have with and also ‘Magnus’ term

Fourier transform where Equation of motion Influence functional Defining We get the equation of motion for the com: and

DYNAMICS OF VORTEX ASSEMBLY We can generalise all this theory to the assembly and find the dynamics. The phase and damping/decoherence terms are more complex, but manageable. For example: Total Phase So that, eg. , the longitudinal Phase terms are where , etc. and etc. Using these equations one can solve for the dynamics of an assembly of vortices, finding the spectrum of collective modes, etc. This takes us too far from this course.

Assembly of Vortices: Consider now an assembly of magnetic vortices, so that Which implies a NON-LOCAL MASS: where (2) ‘Mixed’ memory term: (3) Transverse Damping term: Multi-vortex damping/noise term: with propagator:

see http: //pitp. physics. ubc. ca/
 Pce equation
Pce equation Nchfma
Nchfma Chicago o'hare runway map
Chicago o'hare runway map Simple harmonic motion formulas
Simple harmonic motion formulas Which category of shellfish includes those with tentacles?
Which category of shellfish includes those with tentacles? Ca stamp format
Ca stamp format Recipient company name
Recipient company name Pan-african and independence comprehension check
Pan-african and independence comprehension check Stamp duty(amendment) proclamation no. 612/2008
Stamp duty(amendment) proclamation no. 612/2008 Migratory bird hunting stamp act of 1934
Migratory bird hunting stamp act of 1934 A round purple inspection stamp of refers to
A round purple inspection stamp of refers to Define coupling in software engineering
Define coupling in software engineering 10 usc 1044a notary stamp
10 usc 1044a notary stamp 10 usc 1044a notary stamp
10 usc 1044a notary stamp Trade stamp
Trade stamp Avant testing login
Avant testing login Physics or stamp collecting
Physics or stamp collecting