Optimal SSFP PulseSequence Design For Tissue Segmentation Zhuo

Optimal SSFP Pulse-Sequence Design For Tissue Segmentation Zhuo, ZHENG Advanced Optimization Lab Mc. Master University

Topics • Overview • Model • Optimization Problem • Future Work

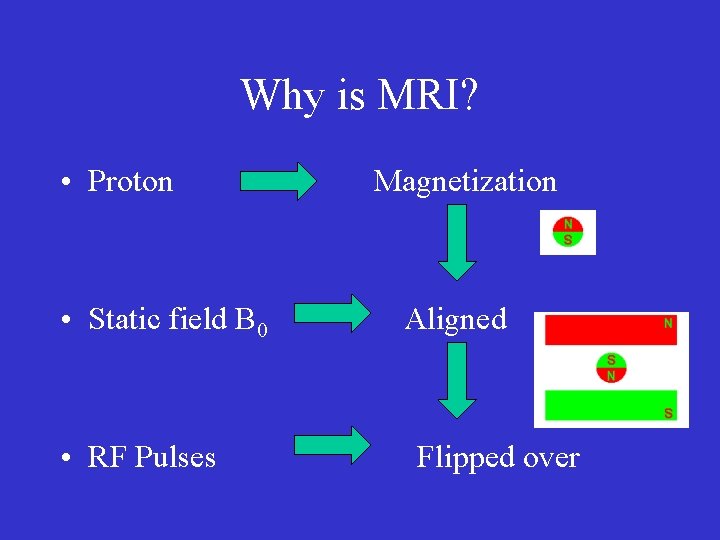
Why is MRI? • Proton • Static field B 0 • RF Pulses Magnetization Aligned Flipped over

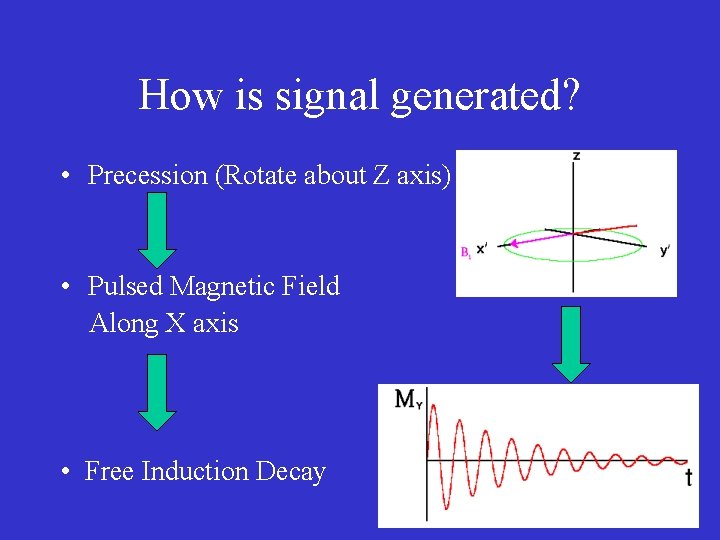
How is signal generated? • Precession (Rotate about Z axis) • Pulsed Magnetic Field Along X axis • Free Induction Decay

How is image reconstructed? • FE & Pulse Sequence • K-Space • Fourier Transformation (Restore Spatial Frequency Info in Place)

Tissue Segmentation Problem • Assuming different tissues combine linearly • Decrease noise by increasing the expected signal amplitude for each tissue • Concerned with min(eigenvalue) of the transformation from the vector space of tissue concentrations to itself given by a change of basis(why? )

Mathematical Model • Approximated by a discrete dynamical system • Magnetization as a unique fix-point (Steady-State) • Explicitly expressed as a function of design variables and parameters of the tissue properties.

Steady-State Signal • Short repetition time, fast scanning, good SNR (Signal-Noise Ratio) • Nontrivial function of many parameters tissue parameters design variables • Dynamic system expression (state-space model): Mk+1 = AMk + B

Reformulation of our Model • Write out A and B explicitly as A= B=

Characteristics of our Model • View steady-state as dynamic equilibrium For consecutive states: Mk+1 = Mk • A is a function of tissue parameters B is a function of design variables • Let Mk+1 = Mk = Mss (conventional notation) Then: (I – A)Mss= B, where (I – A) is nonsingular due to the physical mechanism

Problem Formulation • Transformation from tissue densities to measurements: • Let ε be a vector of measured noise, resulting errors are (STS)-1 STε • We obtain the optimization problem as follows:

Problem Formulation Mss(t, i) corresponding to tissue parameters t and design variables i

Optimization Problem • SDP with highly nonlinear and nonconvex constraints • Objective: choose design variables to minimize error(noise) • Increase ||A|| Decrease ||Mss|| Decrease ||S|| Reduce min(eigenvalue) of STS

How to solve (І) • Brute-force may be useful to get started • Get through all possible permutations of design variables: • Reliable yet time-consuming (number of iterations grows significantly)

Brute-force in our case • Calculate Mss for three different sets of and fill them into S matrix • Do SVD to S and keep updating the maximum of minimum singular value we obtain so far • Output those sets of and the maximum of minimum singular value.

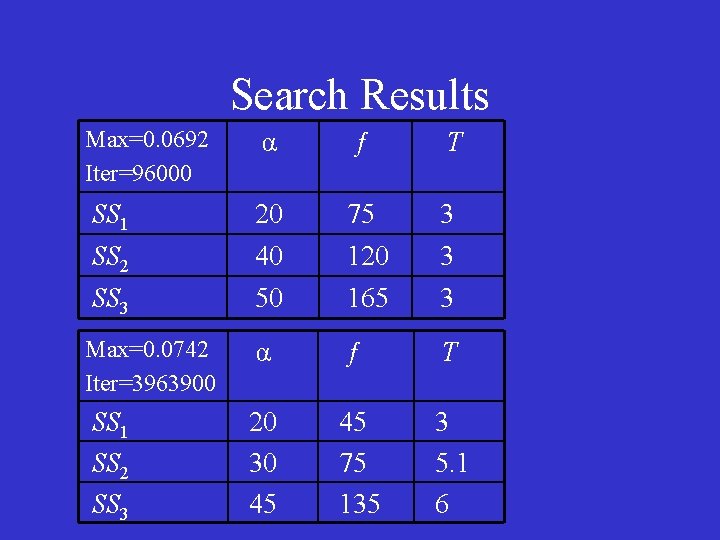
Search Results Max=0. 0692 Iter=96000 α ƒ T SS 1 SS 2 20 40 75 120 3 3 SS 3 50 165 3 Max=0. 0742 Iter=3963900 α ƒ T SS 1 SS 2 SS 3 20 30 45 45 75 135 3 5. 1 6

How to solve (II) • Linearize constraints: Approximate nonlinear constraints by linear or quadratic functions by implicit differentiation and solve in Trust-Region The resulting linear system has the same LHS as the system for finding Mss(not hard to calculate)

Future Work • More precise mathematical model • Applying more sophisticated algorithms to solve the problem • Explore other approaches for tissue segmentation (CG iterative reconstruction based on undersampled raw data)