Operational Semantics Mooly Sagiv http www math tau

Operational Semantics Mooly Sagiv http: //www. math. tau. ac. il/~sagiv/courses/pa. html Tel Aviv University 640 -6706 Sunday 18 -21 Scrieber 8 Monday 10 -12 Schrieber 317 Textbook: Semantics with Applications Chapter 2 H. Nielson and F. Nielson http: //www. daimi. au. dk/~bra 8130/Wiley_book/wiley. html

Outline u Why formal semantics? Possible formal semantics u A Simple programming language While u u u Natural Operational Semantics for While Structural Operational Semantics for While Equivalence Result Extensions to While – – Abort Non determinism Parallel constructs Blocks and procedures

Benefits of Formal Semantics u Programming language design – hard- to-define= hard-to-implement=hard-to-use u Programming language implementation u Programming language understanding u Program correctness u Program equivalence u Compiler Correctness – Correctness of Static Analysis – Design of Static Analysis u Automatic generation of interpreter u But probably not – Automatic compiler generation

Alternative Formal Semantics u Operational Semantics – The meaning of the program is described “operationally” – Natural Operational Semantics – Structural Operational Semantics u Denotational Semantics – The meaning of the program is an input/output relation – Mathematically challenging but complicated u Axiomatic Semantics – The meaning of the program are observed properties

Static Analysis u Automatic derivation of static properties which hold on every execution leading to a program location

Example Static Analysis Problem u Find variables with constant value at a given program location u Example program int p(int x}( return x *x; void main{() } int z; if (getc(() z = p(6) + 8; else z = p(5) + 7; printf (z; ( {

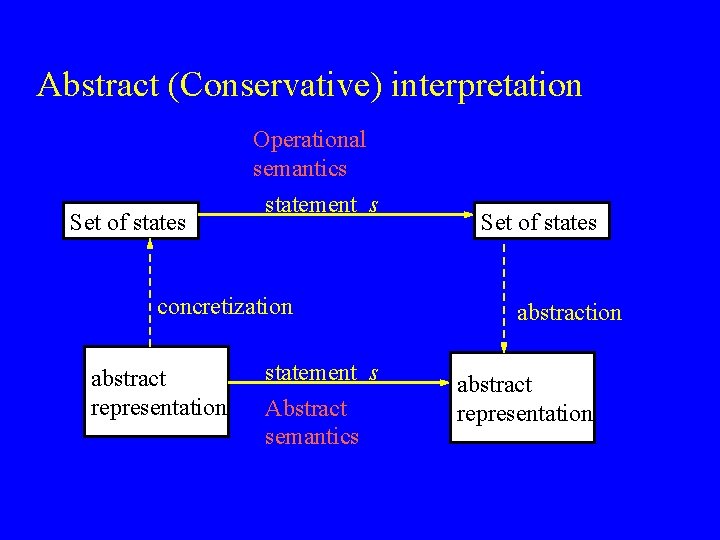
Abstract (Conservative) interpretation Set of states Operational semantics statement s concretization abstract representation statement s Abstract semantics Set of states abstraction abstract representation

Benefits of Operational Semantics for Static Analysis u Correctness (soundness) of the analysis – The compiler will never change the meaning of the program u Establish the right mindset u Design the analysis u Becomes familiar with mathematical notations used in programming languages

The While Programming Language u Abstract syntax S: : = x : = a | skip | S 1 ; S 2 | if b then S 1 else S 2 | while b do S u Use parenthesizes for precedence u Informal Semantics – skip behaves like no-operation – Import meaning of arithmetic and Boolean operations

Example While Program y : = 1; while (x=1) do) y : = y * x; x : = x - 1 (

General Notations u Syntactic – – Var the set of program variables Aexp the set of arithmetic expressions Bexp the set of Boolean expressions Stm set of program statements u Semantic – – – categories Natural values N={0, 1, 2… , Truth values T={ff, tt{ States S= Var N Lookup in a state s: s x Update of a state s: s [ x 5[

Natural Operational Semantics u Describe the “overall” effect of program constructs u Ignores non terminating computations

Natural Semantics u Notations – >S, s> - the program statement S is executed on input state s – s representing a terminal (final) state u For every statement S, write meaning rules <S, i> o “If the statement S is executed on an input state i, it terminates and yields an output state o” u The meaning of a program P on an input state s is the set of outputs states o such that <P, i> o u The meaning of compound statements is defined using the meaning immediate constituent statements

Natural Semantics for While ]ass ] <x : = a, s> s[x ns axioms rules A a s[ ]skipns] <skip, s> s ]compns] <S 1 , s> s’, <S 2, s’> s’’ > S 1; S 2, s> s ’’ ]ifttns] <S 1 , s> s’ > if b then S 1 else S 2, s> s ’ ]ifffns] <S 2 , s> s’ > if b then S 1 else S 2, s> s ’ if B b s=tt if B b s=ff

Natural Semantics for While (More rules( ]whilettns] <S , s> s’, <while b do S, s’> s’’ <while b do S, s> s ’’ ]whileffns] <while b do S, s> s if B b s=tt if B b s=ff

Simple Examples u Let s 0 be the state which assigns zero to all program variables u Assignments [assns] <x : = x+1, s 0> s 0[x 1 [ u Skip statement [skipns] <skip, s 0> s 0 u Composition ]compns] <skip , s 0> s 0, <x : = x+1, s 0> s 0[x 1[ > skip; x : = x +1, s 0> s 0[x 1 [

Simple Examples (Cont( u Let s 0 be the state which assigns zero to all program variables u if-construct ]ifttns] > <skip , s 0> s 0 if x=0 then skip else x : = x +1, s 0> s 0

A Derivation Tree “proof” that <S, s> s’ u The root of tree is <S, s> s’ u Leaves are instances of axioms u Internal nodes rules u. A – Immediate children match rule premises u Simple Example >skip; x : = x +1, s 0> s 0[x 1<[ >skip, s 0> s 0 >x : = x +1, s 0> s 0[x 1<[

An Example Derivation Tree )>x : =x+1; y : =x+1) ; z : = y), s 0> s 0[x 1][y 2][z 2[

Top Down Evaluation of Derivation Trees u Given a program S and an input state s u Find an output state s’ such that <S, s> s’ u Start with the root and repeatedly apply rules until the axioms are reached u Inspect different alternatives in order u In While s’ and the derivation tree is unique

Example of Top Down Tree Construction u Input state s such that s x = 3 u Factorial program y : = 1; while (x=1) do (y : = y * x; x : = x - 1(

Program Termination u Given a statement S and input s – S terminates on s if there exists a state s’ such that <S, s> s’ – S loops on s if there is no state s’ such that <S, s> s’ u Given a statement S – S always terminates if for every input state s, S terminates on s – S always loops if for every input state s, S loops on s

Properties of Natural Semantics u Equivalence of program constructs – “skip ; skip” is semantically equivalent to “skip” – ))“S 1 ; S 2) ; S 3)” is semantically equivalent to “(S 1 ; ( S 2 ; S 3”(( – )“x : = 5 ; y : = x * 8)” is semantically equivalent to “(x : =5; y : = 40”( u Deterministic – If <S, s> s 1 and <S, s> s 2 then s 1=s 2

Semantic Equivalence u S 1 and S 2 are semantically equivalent if for all s and s’ <S 1, s> s’ if and only if <S 2, s> s ’ u Simple example “while b do S” is semantically equivalent to: “if b then (S ; while b do S) else skip”

Deterministic Semantics for While If <S, s> s 1 and <S, s> s 2 then s 1=s 2 u The proof uses induction on the shape of derivation trees u – Prove that the property holds for all simple derivation trees by showing it holds for axioms – Prove that the property holds for all composite trees : » For each rule assume that the property holds for its premises (induction hypothesis) and prove it holds for the conclusion of the rule

The Semantic Function Sns u The meaning of a statement S is defined as a partial function from State to State u Sns: Stm (State State( u Sns S s = s’ if <S, s> s’ and otherwise Sns S s is undefined u Examples – Sns skip s =s – Sns x : =1 s = s [x 1[ – Sns while true do skip s = undefined

Structural Operational Semantics u u u Emphasizes the individual steps Usually more suitable for analysis For every statement S, write meaning rules <S, i> “If the first step of executing the statement S on an input state i leads to ” Two possibilities for – = <S’, s’> The execution of S is not completed, S’ is the remaining computation which need to be performed on s ’ – = o The execution of S has terminated with a final state o – is a stuck configuration when there are no transitions The meaning of a program P on an input state s is the set of final states that can be executed in arbitrary finite steps

Structural Semantics for While ]ass ] <x : = a, s> s[x sos axioms rules A a s[ ]skipsos] <skip, s> s ]comp 1 sos] <S 1 , s> <S’ 1, s<’ > S 1; S 2, s> < S’ 1; S 2, s <’ ]comp 2 sos] <S 1 , s> s’ > S 1; S 2, s> < S 2, s <’

Structural Semantics for While if construct <if b then S 1 else S 2, s> <S 1, s < if B b s=tt ]ifffos] <if b then S 1 else S 2, s> <S 2, s < if B b s=ff ]iftt sos]

Structural Semantics for While while construct ]whilesos] <while b do S, s> <if b then (S; while b do S) else skip, s <

Derivation Sequences u. A finite derivation sequence starting at <S, s> 0, 1, 2 …, k such that – 0=<S, s < – i i+1 – k is either stuck configuration or a final state u An infinite derivation sequence starting at <S, s> 0, 1, 2 … such that – 0=<S, s < – i i+1 u 0 i i in i steps u 0 * i in finite number of steps u For each step there is a derivation tree

Example u Let s 0 such that s 0 x = 5 and s 0 y = 7 u S = (z: =x; x : = y); y : = z

Factorial Program u Input state s such that s x = 3 u y : = 1; while (x=1) do (y : = y * x; x : = x - 1(

Program Termination u Given a statement S and input s – S terminates on s if there exists a finite derivation sequence starting at <S, s< – S terminates successfully on s if there exists a finite derivation sequence starting at <S, s> leading to a final state – S loops on s if there exists an infinite derivation sequence starting at <S, s<

Properties of the Semantics u S 1 and S 2 are semantically equivalent if: – for all s and s’ <S 1, s> * s’ if and only if <S 2, s> *s’ – there is an infinite derivation sequence starting at <S 1, s> if and only if there is an infinite derivation sequence starting at <S 2, s < u Deterministic – If <S, s> * s 1 and <S, s> * s 2 then s 1=s 2 u The execution of S 1; S 2 on an input can be split into two parts: – execute S 1 on s yielding a state s’ – execute S 2 on s ’

Sequential Composition u If <S 1; S 2, s> k s’’ then there exists a state s’ and numbers k 1 and k 2 such that – >S 1, s> k 1 s’ – >S 2, s’> k 2 s’’ – and k = k 1 + k 2 u The proof uses induction on the length of derivation sequences – Prove that the property holds for all derivation sequences of length 0 – Prove that the property holds for all other derivation sequences : » Show that the property holds for sequences of length k+1 using the fact it holds on all sequences of length k (induction hypothesis(

The Semantic Function Ssos u The meaning of a statement S is defined as a partial function from State to State u Ssos: Stm (State State( u Ssos S s = s’ if <S, s> *s’ and otherwise Ssos S s is undefined

An Equivalence Result u For every statement S of the While language – Snat S = Ssos S

Extensions to While u Abort statement (like C exit( u Non determinism u Parallelism u Local Variables u Procedures – Static Scope – Dynamic scope

The While Programming Language with Abort u Abstract syntax S: : = x : = a | skip | S 1 ; S 2 | if b then S 1 else S 2 | while b do S| abort u Abort terminates the execution u No new rules are needed in natural and structural operational semantics u Statements – skip – abort – while true do skip

Conclusion u The natural semantics cannot distinguish between looping and abnormal termination (unless the states are modified ( u In the structural operational semantics looping is reflected by infinite derivations and abnormal termination is reflected by stuck configuration

The While Programming Language with Non-Determinism u Abstract syntax S: : = x : = a | skip | S 1 ; S 2 | if b then S 1 else S 2 | while b do S| S 1 or S 2 u Either S 1 or S 2 is executed u Example – x : = 1 or (x : =2 ; x : = x+2(

The While Programming Language with Non-Determinism Natural Semantics ]or 1 ns] <S 1 , s> s’ > S 1 or S 2, s> s’ ]or 2 ns] <S 2 , s> s’ > S 1 or S 2, s> s’

The While Programming Language with Non-Determinism Structural Semantics

The While Programming Language with Non-Determinism Examples x : = 1 or (x : =2 ; x : = x+2( u )while true do skip) or (x : =2 ; x : = x+2( u

Conclusion u In the natural semantics non-determinism will suppress looping if possible (mnemonic ( u In the structural operational semantics nondeterminism does suppress termination configuration

The While Programming Language with Parallel Constructs u Abstract syntax S: : = x : = a | skip | S 1 ; S 2 | if b then S 1 else S 2 | while b do S| S 1 par S 2 u All the interleaving of S 1 or S 2 are executed u Example – x : = 1 or (x : =2 ; x : = x+2(

The While Programming Language with Parallel Constructs Structural Semantics ]par 1 sos] <S 1 , s> <S’ 1, s<’ > S 1 par S 2, s> < S’ 1 par S 2, s <’ ]par 2 sos] <S 1 , s> , s’ > S 1 par S 2, s> < S 2, s <’ ]par 3 sos] <S 2 , s> <S’ 2, s<’ > S 1 par S 2, s> < S 1 par S’ 2, s <’ ]par 4 sos] <S 2 , s> , s’ > S 1 par S 2, s> < S 1, s <’

The While Programming Language with Parallel Constructs Natural Semantics

Conclusion u In the natural semantics immediate constituent is an atomic entity so we cannot express interleaving of computations u In the structural operational semantics we concentrate on small steps so interleaving of computations can be easily expressed

Conclusions Local Variables u The natural semantics can “remember” local states u Need to introduce stack or heap into state of the structural semantics