On Updating Torsion Angles of Molecular Conformations Vicky



















- Slides: 29

On Updating Torsion Angles of Molecular Conformations Vicky Choi Department of Computer Science Virginia Tech (with Xiaoyan Yu, Wenjie Zheng) 1

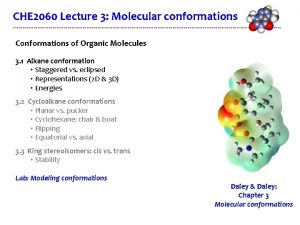
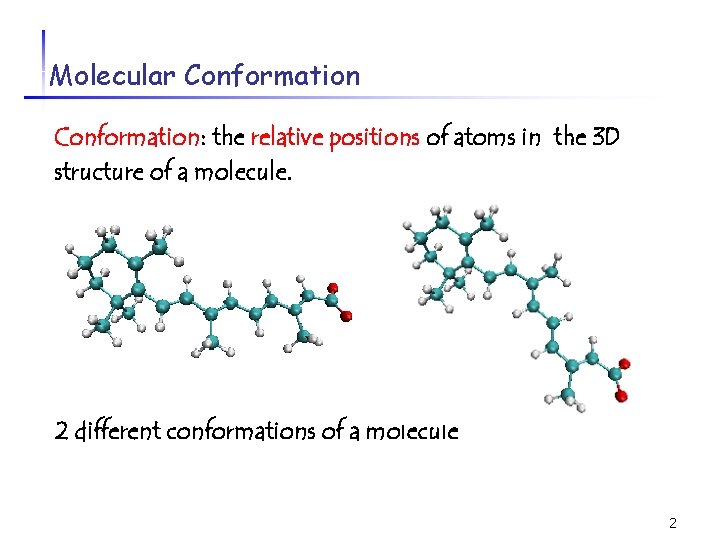
Molecular Conformation: the relative positions of atoms in the 3 D structure of a molecule. 2 different conformations of a molecule 2

Representations of Molecular Conformation - Cartesian Coordinates e. g. PDB, Mol 2 - Distance Matrix - Internal Coordinates Ø Bond length, bond angle, torsion angle Ø E. g. Z-Matrix 3

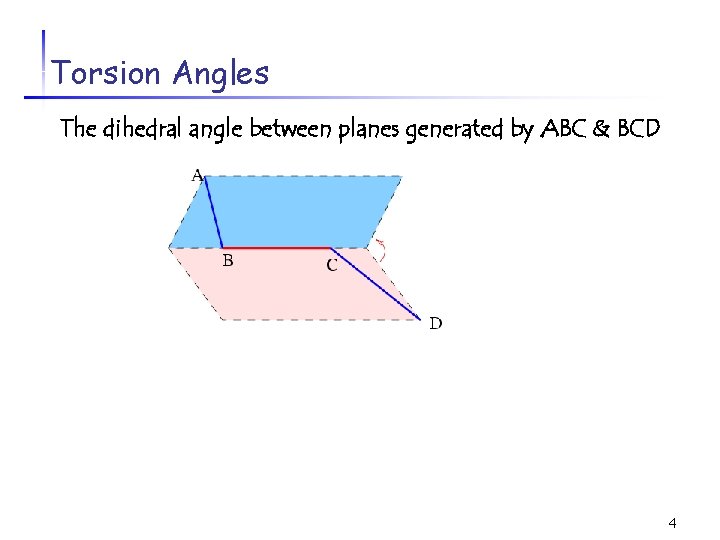
Torsion Angles The dihedral angle between planes generated by ABC & BCD C 4

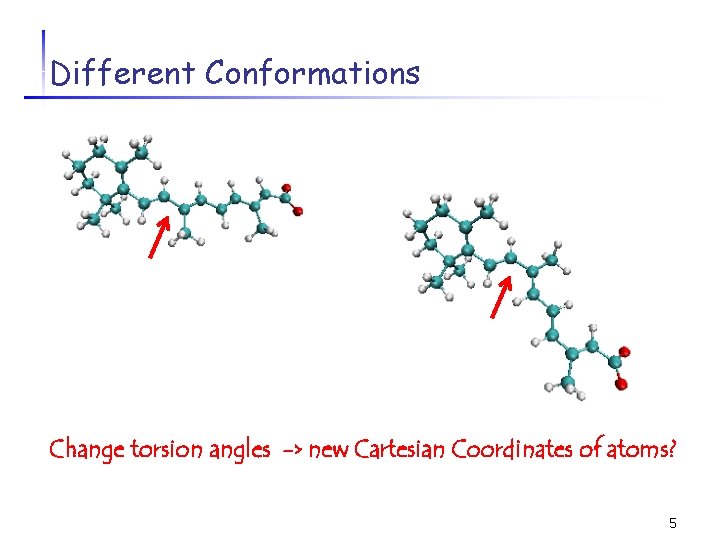
Different Conformations Change torsion angles -> new Cartesian Coordinates of atoms? 5

Rotatable bonds - single bond - acyclic (non-ring) bond - not connects to a terminal atom 6

Rotation (Mathematical Definition) - Isometry: a transformation from R 3 to R 3 that preserves distances - Rotation: an orientation-preserving isometry with the ORIGIN fixed Ø A rotation in R 3 can be expressed by an orthonormal matrix with determinant +1 – rotation matrix - Let b 2 R 3 and b' be the image of b after rotation R b’= Rb 7

Rotation - Geometrically, a rotation is performed by an angle about a rotation axis ov through ORIGIN - R: rotation matrix - rotation axis ov : - v is the eigenvector corresponding to the eigenvalue +1 (Rv=v) rotation angle: = arcos((Tr(R)-1)/2) 8

Unit Quaternion - q=(q 0, qx, qy, qz) unit vector in R 4 - rotation angle - v=(vx, vy, xz) the unit vector along the rotation axis - (through origin) q 0=cos( /2), (qx, qy, qz)=sin( /2) v Let b 2 R 3 and b' be the image of b after rotation q. 9

Unit Quaternion Hypercomplex q=(q 0, qx, qy, qz) q = q 0 + i ¢ qx + j ¢ qy + k ¢ qz Multiplication rules: i 2=j 2=k 2=-1 ij=k, ji=-k, jk=I, kj=-i, ki=j, ik=-j 10

Rigid Motion - Represented by a rotation followed by a translation - Representations: Ø 4 x 4 Homogenous matrix: Ø Quaternion-vector form : [q, t] 11

Representation of Bond Rotation - Rotate about the rotatable bond bi, rotate by i Rotatable bond bi is not necessarily going through the origin 1. Translation (by –Qi such that Qi becomes origin) 2. Rotation (unit vector along bi, rotation angle= i) 3. Translation back 12

Representation of Bond Rotation b’ = Ri(b-Qi) + Qi = Ri(b) + Qi – Ri(Qi) The rigid motion: Rotation part Translation part In quaternion-vector form: In homogenous matrix form: 13

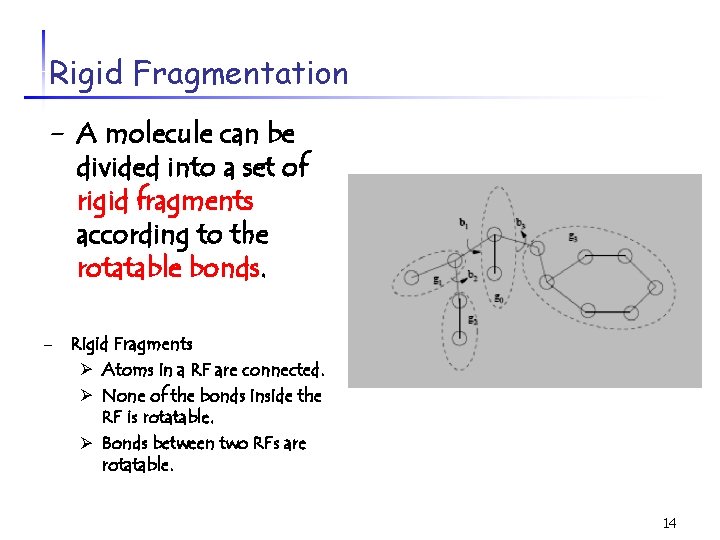
Rigid Fragmentation - A molecule can be divided into a set of rigid fragments according to the rotatable bonds. - Rigid Fragments Ø Atoms in a RF are connected. Ø None of the bonds inside the RF is rotatable. Ø Bonds between two RFs are rotatable. 14

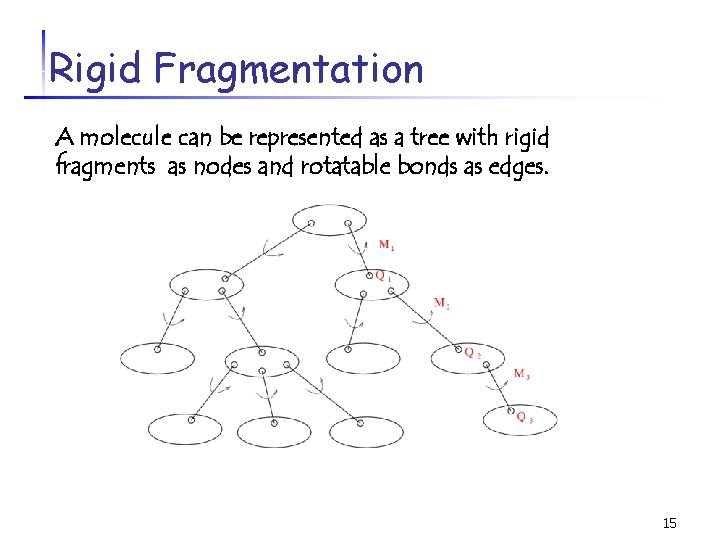
Rigid Fragmentation A molecule can be represented as a tree with rigid fragments as nodes and rotatable bonds as edges. 15

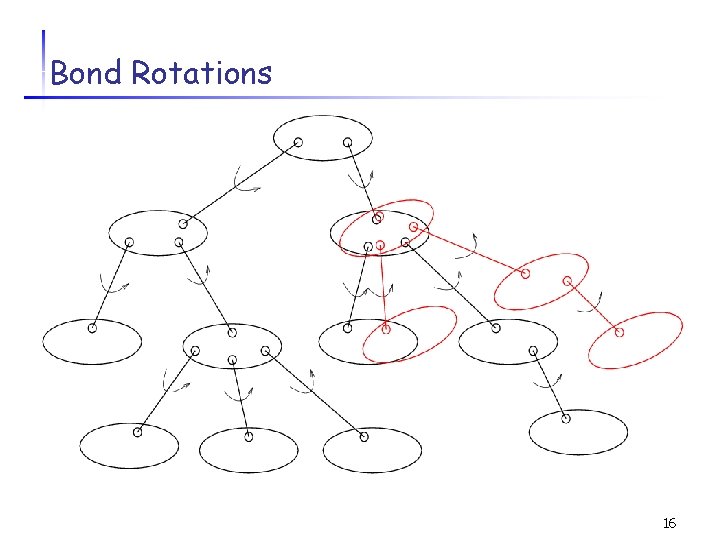
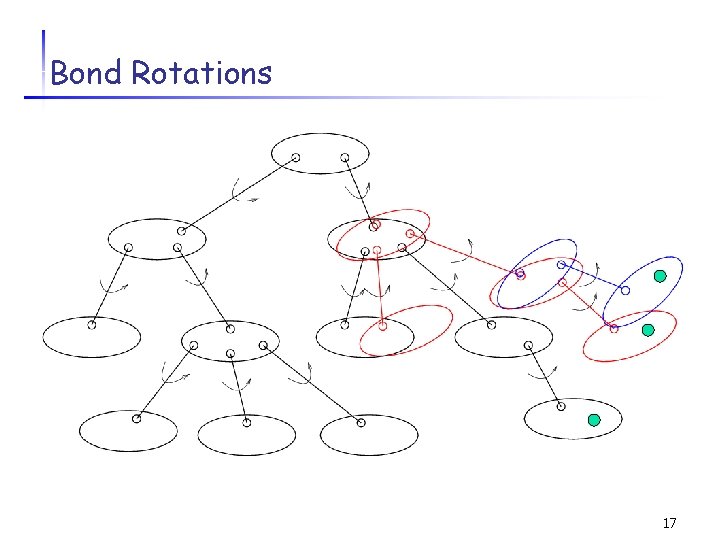
Bond Rotations 16

Bond Rotations 17

(1) Simple Rotations - Rotatable bonds: b 1, b 2, …, bi - Rotation angles: 1, 2, …, i -Atoms are updated by a series of rigid transformations (corresponding to rotations about rotatable bonds). -Let Mi be the ith rigid motion(rotate about bond bi by angle i): (x’, y’, z’, 1)T = Mi. Mi-1…M 1(x, y, z, 1)T 18

Time Complexity - Ni = Mi Mi-1 … M 1, Mi=[qi, Qi – qi. Qiqi] - Ni+1 = Mi+1 Ni - It takes constant time to compute Mi+1, and constant - time to compute Ni+1 from Ni Let nrb be # of rotatable bonds; na be the # of atoms Total time: O(nrb) (compute all the rigid motions) + O(na) (update positions of all atoms) Zheng & Kavraki: A new method for fast and accurate derivation of molecular conformations. Journal of Chemical Information and Computer Sciences, 42, 2002. # of multiplications: 75 nrb + 9 na (using homogenous matrices) 19

Our Improvement - Simple Rotations where - Improved Simple Rotations # multiplications : 50 nrb+9 na 20

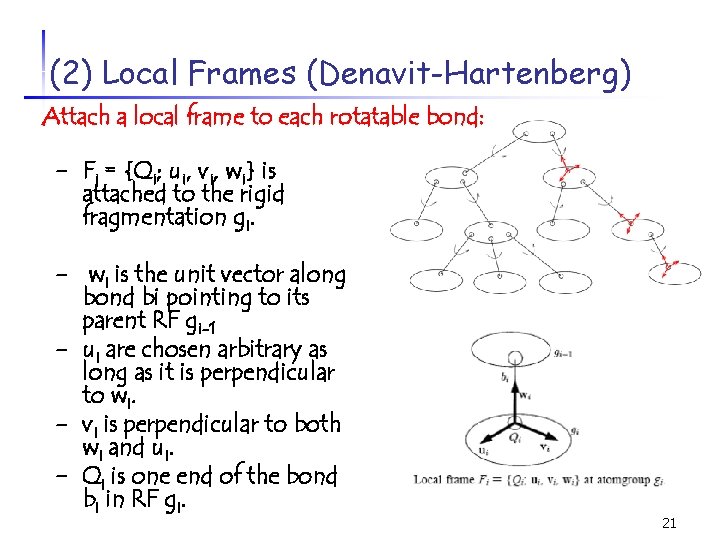
(2) Local Frames (Denavit-Hartenberg) Attach a local frame to each rotatable bond: - Fi = {Qi; ui, vi, wi} is attached to the rigid fragmentation gi. - wi is the unit vector along - bond bi pointing to its parent RF gi-1 ui are chosen arbitrary as long as it is perpendicular to wi. vi is perpendicular to both wi and ui. Qi is one end of the bond bi in RF gi. 21

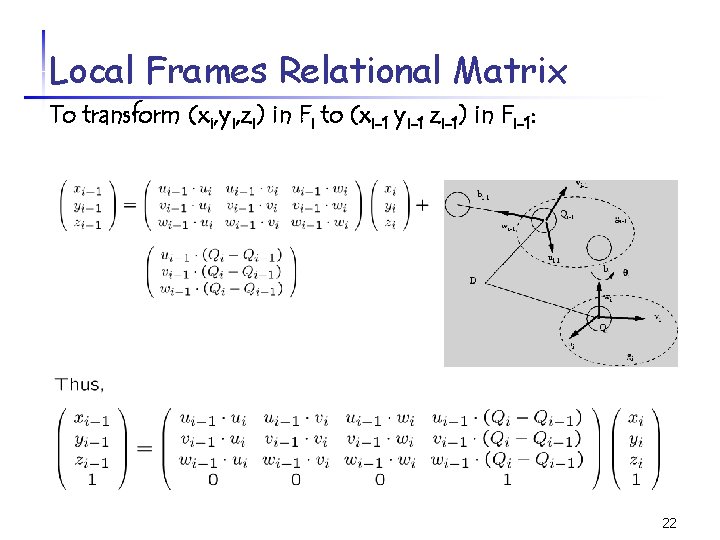
Local Frames Relational Matrix To transform (xi, yi, zi) in Fi to (xi-1 yi-1 zi-1) in Fi-1: 22

Local Frames Relational Matrix Pi is rigid motion invariant and can be precomputed! 23

Local Frames Contd. -We get the corresponding position of (xi’, yi’, zi’) in Fi-1 24

Local Frames The coordinates of an atom in local frame Fi can be represented in global frame after a series of transformations: (x', y', z', 1)T = M 1 M 2 … Mi (x, y, z, 1)T 25

Global Frame (Simple Rotations) vs Local Frames - Global Frame: (x’, y’, z’, 1)T = Mi. Mi-1…M 1(x, y, z, 1)T - Local Frames: (x', y', z', 1)T = M 1 M 2 … Mi (x, y, z, 1)T 26

Comparison nrb – the number of rotatable bonds Simple rotations implemented by Zheng & Kavraki # multiplicatio ns (nrb) 75 Local Frames by Zheng & Kavraki 48 Improved simple rotations in unit quaternion 50 27

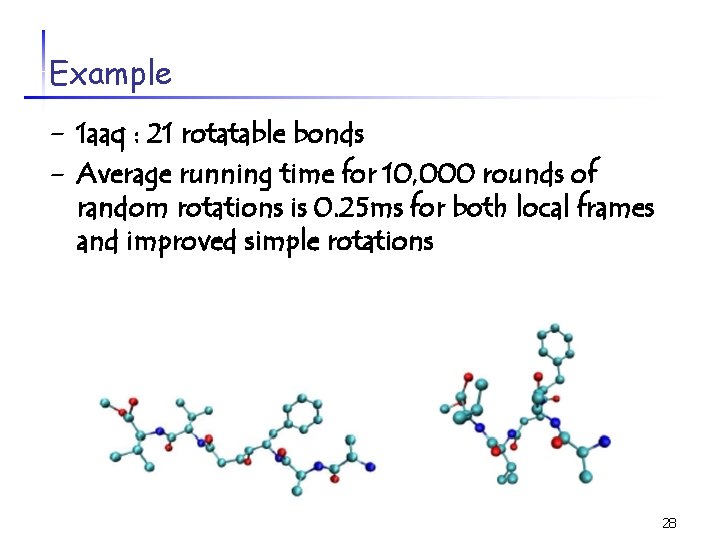
Example - 1 aaq : 21 rotatable bonds - Average running time for 10, 000 rounds of random rotations is 0. 25 ms for both local frames and improved simple rotations 28

Conclusions - Computational cost is almost the same but local frames require precomputations of a series of local frames relational matrices - Local Frames: Lazy look up (don’t need to compute ancestor atoms, but need to compute a sequence of local frames relational matrices) - Conformer generator 29
 Database commit is triggered by
Database commit is triggered by Properties of vertically opposite angles
Properties of vertically opposite angles Drawing chair conformations
Drawing chair conformations Conformations
Conformations The updating of accounts is called the adjusting process.
The updating of accounts is called the adjusting process. Sccm cluster aware updating
Sccm cluster aware updating Batch updating (for oca & db)
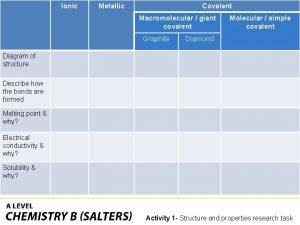
Batch updating (for oca & db) Ionic covalent metallic
Ionic covalent metallic Giant molecular structure vs simple molecular structure
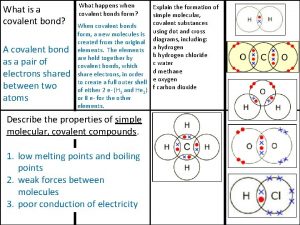
Giant molecular structure vs simple molecular structure Covalent bond
Covalent bond Angle vicky
Angle vicky Tina maier
Tina maier Vicky i proof
Vicky i proof Vicky thorland-oster
Vicky thorland-oster Vicky beeching
Vicky beeching Vicky verb
Vicky verb Sarah jacobson williams
Sarah jacobson williams Assistant director vicky
Assistant director vicky Bethnal green police station
Bethnal green police station Vicky varela
Vicky varela Vicky ferguson
Vicky ferguson Shrek vicky jenson
Shrek vicky jenson Vicky hines
Vicky hines Vicky boy resort
Vicky boy resort Queen vicky
Queen vicky Vicky kelly
Vicky kelly Ucf timesheet
Ucf timesheet Vicky kaspi
Vicky kaspi Vicky pope
Vicky pope Vicky hines
Vicky hines