Oknkov Fourierova transformace translace dilatace a 0 R

Okénková Fourierova transformace translace, dilatace a > 0, R R waveletová transformace

Waveletová transformace h a, => a, b - matečná waveleta (mother wavelet) - wave. . . osciluje - …. let dobře lokalizovaná kolem 0, mizí rychle 2 - =0 <∞ - | |2 < a, b x-b a > 0, R b R, normalizace přes škály - FT( ) a, b v 0 - 0, v - 0 - něco jako band-pass filtr ve FT

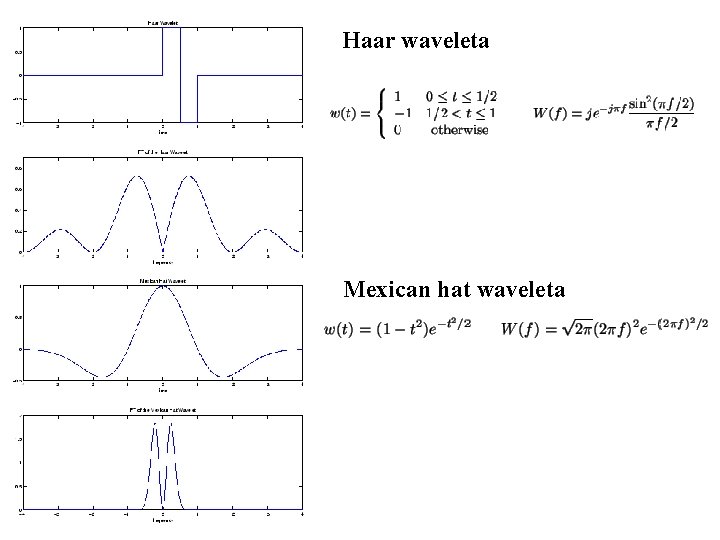
Haar waveleta Mexican hat waveleta

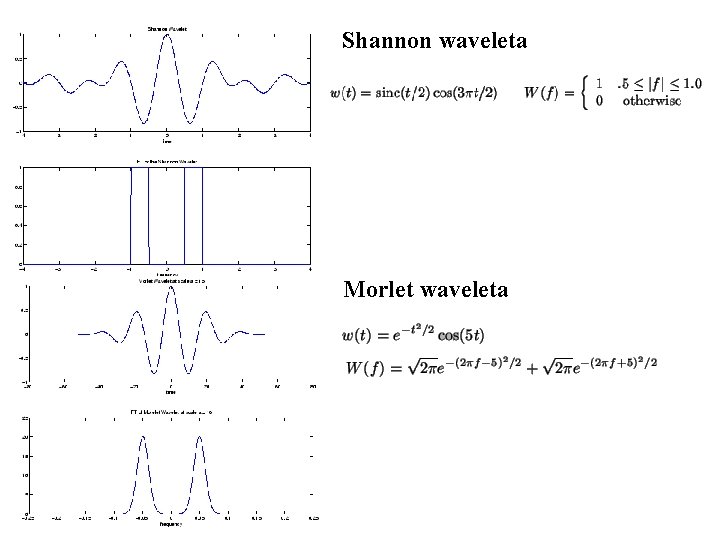
Shannon waveleta Morlet waveleta

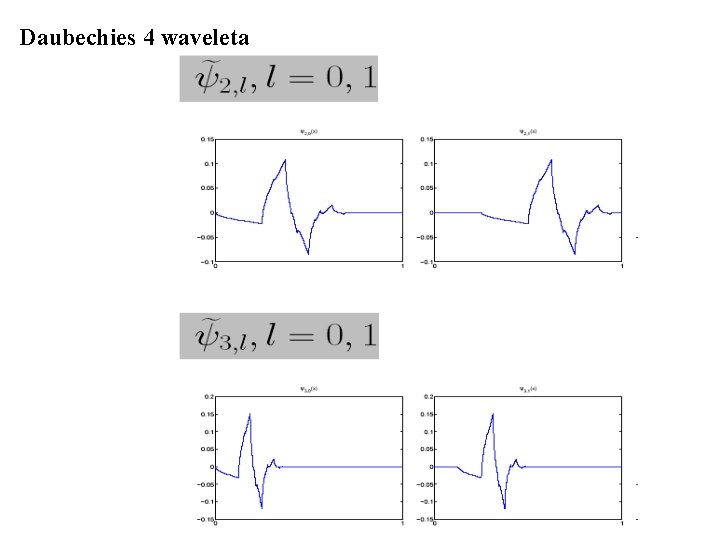
Daubechies 4 waveleta

Spojitá waveletová transformace a, b* a, b c - záleží na a > 0, R b R a, b WF(a, b) = f (t), a, b REDUNDANTNÍ!! – diskretizace a, b

Dyadická síť – diskretizace a, b • „time“ vzorkování u nízkých frekvencí – řídké stačí b log a a vzorkované na log stupnici b vzorkované hustěji u malého a obvykle a 0 = 2 a b 0 = 1, což vede na dyadickou síť

Dyadická waveletová transformace - waveletové řady a, b binární škálování dyadický posun m, n - - zmenšování o faktor 2 - posun o k/2 j x-b - < m, n Z ortonormální báze L 2(R) m, n , k, l = m, k n, l f(x) = c m, n , m, n - - c m, n = f (x), m, n Přeurčenost

Diskrétní waveletová transformace - cesta Kompaktní dyadická waveletová transformace - f(x), m, n nenulové na [0, 1], jednotkový interval j j = 2 m + n, m = 0, 1, … n = 0, 1, … 2 j - 1 pro libovolné j je m je největší takové, že 2 m j, n = j - 2 m f(x) = c j , j - c j = f (x), j Diskretizace f N vzorků spojité … f (i x) … mocnina 2

Diskrétní waveletová transformace Kompaktní dyadická waveleta Diskretizace f …. f (i x) N vzorků … mocnina 2 j N f(x) = c j , j 1 N c j = f (x), j = f(x) j 1 diskrétní

FT - spojitá funkce x spojitá funkce FŘ - periodická funkce x řada koeficientů DFT - navzorkovaná funkce x navzorkované spektrum SWT - spojitá funkce x spojité a, b WŘ - spojitá funkce x řada koeficientů DWT - navzorkovaná funkce x konečná řada koeficientů

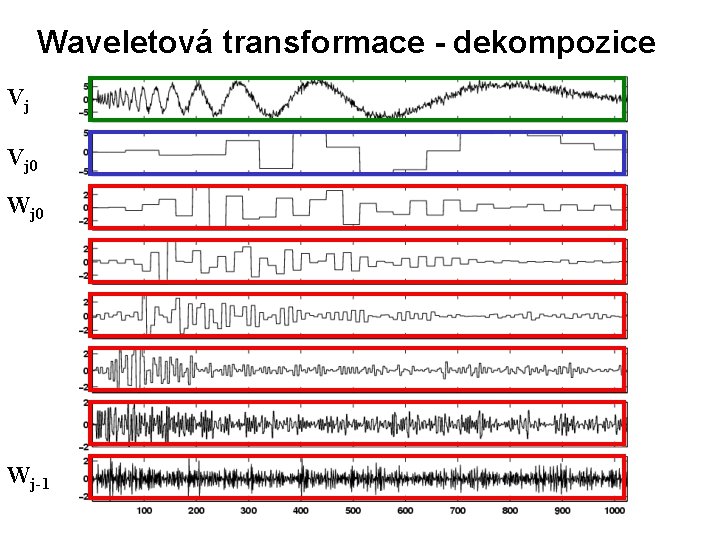
Waveletová transformace - dekompozice

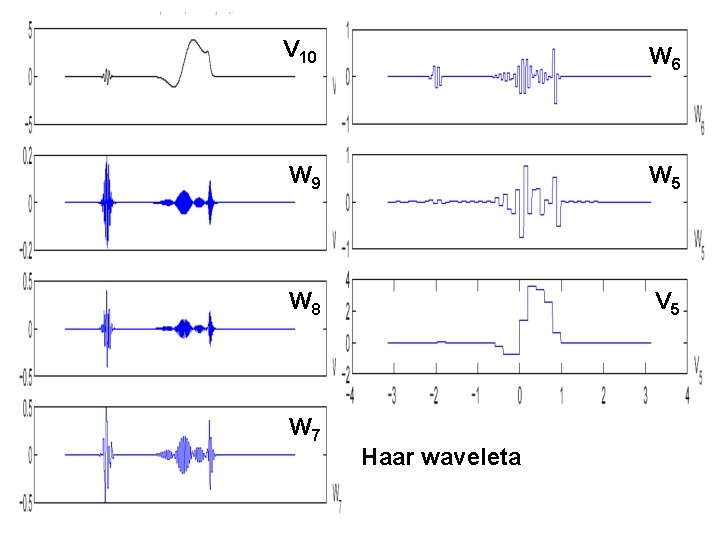
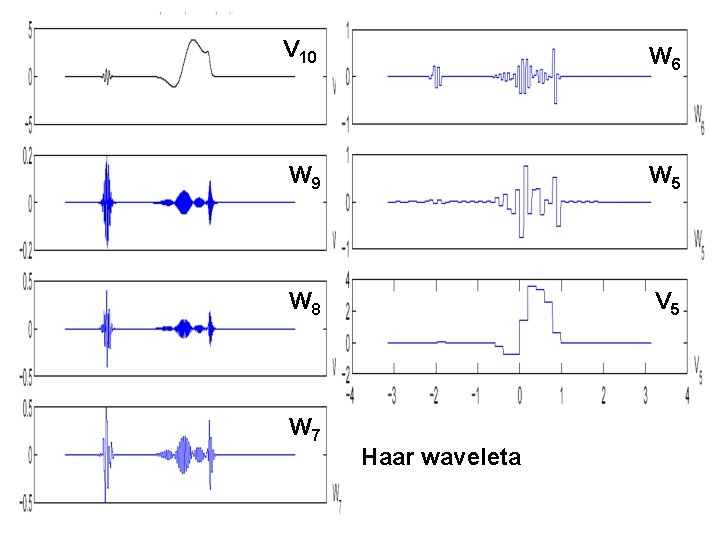
V 10 W 6 W 9 W 5 W 8 V 5 W 7 Haar waveleta

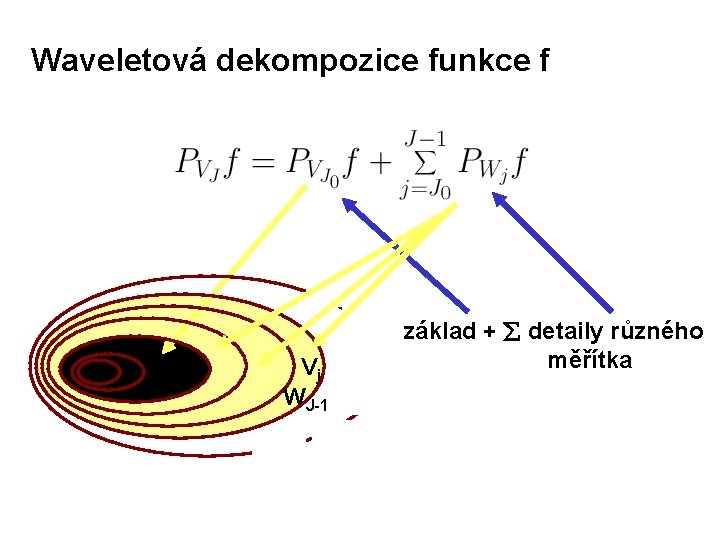
Waveletová dekompozice funkce f Vj 0 Vj WJ-1 základ + detaily různého měřítka

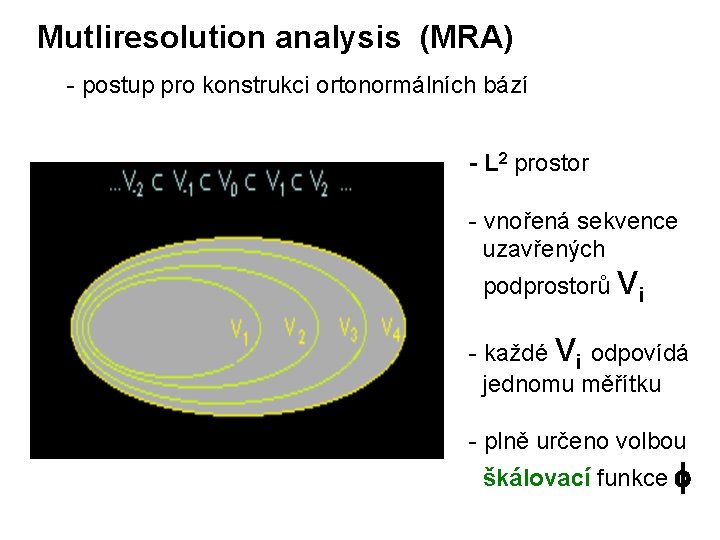
Mutliresolution analysis (MRA) - postup pro konstrukci ortonormálních bází - L 2 prostor - vnořená sekvence uzavřených podprostorů Vi - každé Vi odpovídá jednomu měřítku - plně určeno volbou škálovací funkce

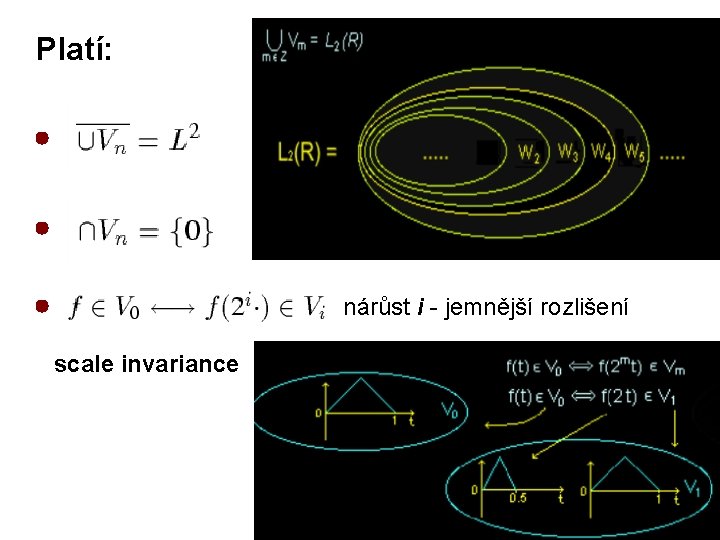
Platí: nárůst i - jemnější rozlišení scale invariance

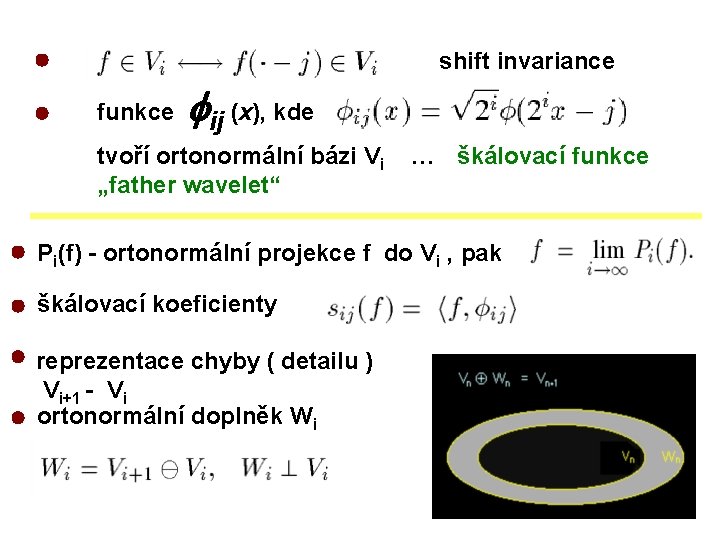
shift invariance funkce ij (x), kde tvoří ortonormální bázi Vi „father wavelet“ … škálovací funkce Pi(f) - ortonormální projekce f do Vi , pak škálovací koeficienty reprezentace chyby ( detailu ) Vi+1 - Vi ortonormální doplněk Wi

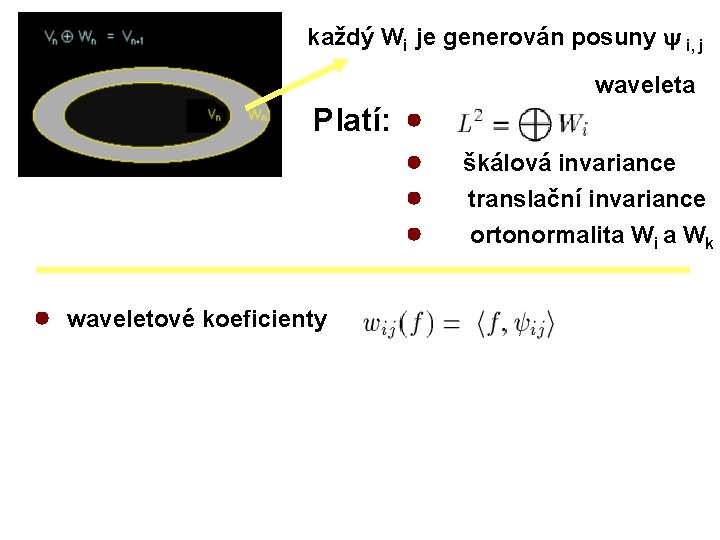
každý Wi je generován posuny i, j waveleta Platí: škálová invariance translační invariance ortonormalita Wi a Wk waveletové koeficienty

Waveletová transformace - dekompozice Vj Vj 0 Wj-1

škálovací koeficienty waveletové koeficienty … vyhlazovací (smoothing) funkce - nenulový (=1) - =0 - a FT( ) dobrý pokles ( lokalizace v obou oblastech) - kompaktní , - nulové krom určitého konečného intervalu

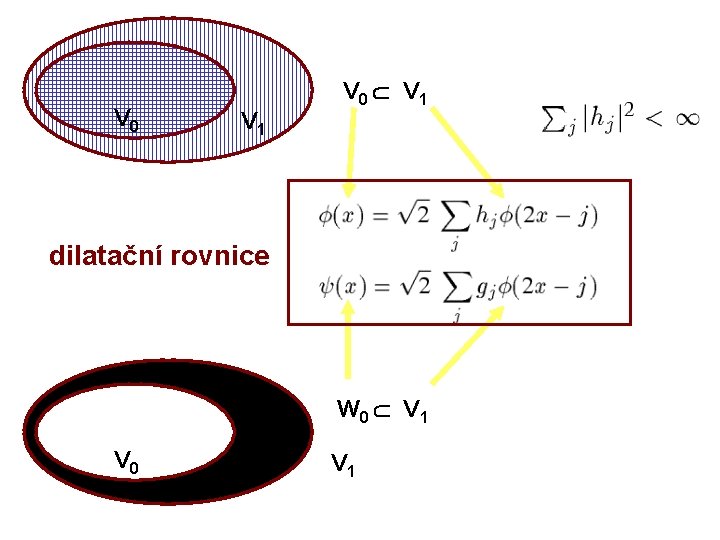
V 0 V 1 V 0 V 1 dilatační rovnice W 0 V 1 V 0 W 0 V 1

Haar waveleta h=[ , ] g=[ , - ]

Poznámky k h a g h, g quadrature mirror filtry (|H|2 + |G|2 = 1) h - low pass filtr g - high pass filtr g h=[ , ] g=[ , - ] h = 2 g= 0 – h zpětně se změněnými znaménky posun o pul periody h. N-1 -j = (-1) j g = [h 3 -h 2 h 1 -h 0] hj určuje škálovací funkci

Ortogonalita waveleta (wavelet) báze Wi škálovací funkce (scaling function) báze Vi

Waveletová dekompozice funkce f Vj 0 Vj základ + detaily různého měřítka

V 10 W 6 W 9 W 5 W 8 V 5 W 7 Haar waveleta

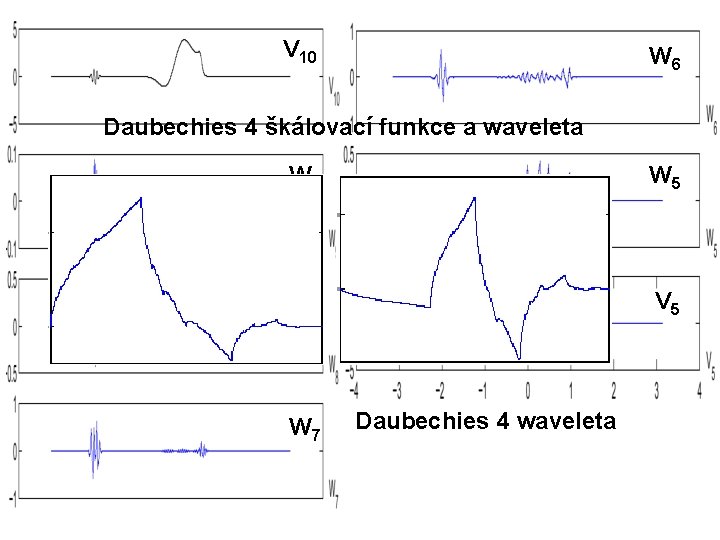
V 10 W 6 Daubechies 4 škálovací funkce a waveleta W 9 W 5 W 8 V 5 W 7 Daubechies 4 waveleta

V 10 W 6 W 9 W 5 W 8 V 5 W 7 Haar waveleta

Waveletová dekompozice funkce f PVjf - ortonormální projekce f do Vi kompaktní suport základ + detaily různého měřítka

Vj Vj-1 + Wj-1 (PV f )(x) = cj-1, k(x) + dj-1, k (x) j k k DR cj-1, k = h(n-2 k) cj, n n dj-1, k = g(n-2 k) cj, n n cj+1, k = h(k-2 l) cj, l + g(k-2 l) dj, l l signál délky 2 J - vzorky na jednotkovém intervalu Vn < f, J, k >, aproximace spojité funkce f. . c. J, k

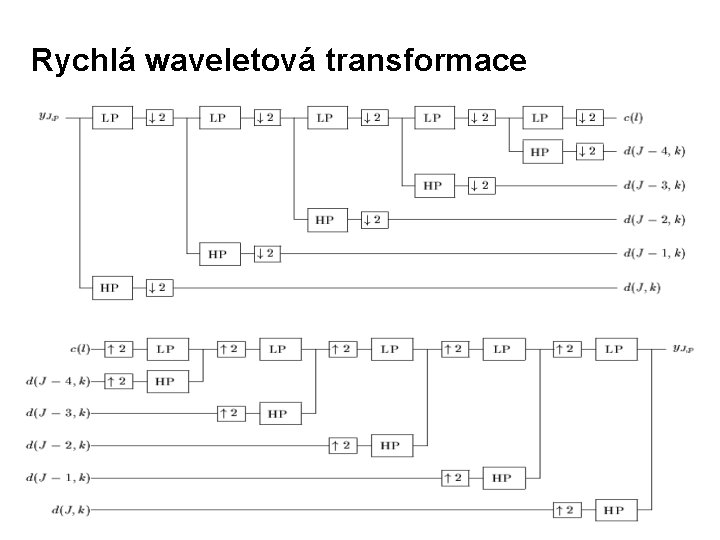
Rychlá waveletová transformace

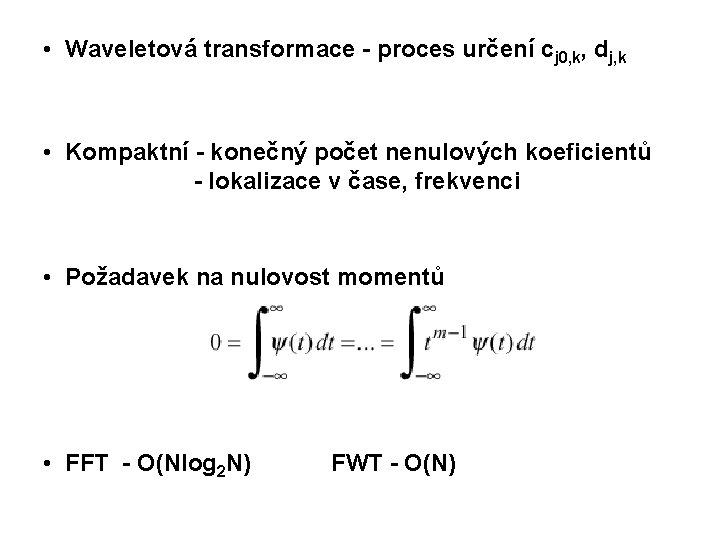
• Waveletová transformace - proces určení cj 0, k, dj, k • Kompaktní - konečný počet nenulových koeficientů - lokalizace v čase, frekvenci • Požadavek na nulovost momentů • FFT - O(Nlog 2 N) FWT - O(N)

• Vlastnosti očekávané od wavelet - dobrá lokalizace - jednoduchost konstrukce a reprezentace - invariance vzhledem k některým operacím - hladkost, spojitost, diferencovatelnost, symetrie - dobré vlastnosti vzhledem k počtu nulových momentů

Kompaktnost - v obrazové oblasti (ve frekvenční rychle k nule) - nižší výpočetní nároky - lepší obrazové rozlišení x horší frekvenční Symetrie - ortogonální kompaktní wavelety nemohou být sym. - biortogonální wavelety Momenty a jejich nulovost 1. M momentů 0 : signály typu nulové detailní koeficienty dobré pro kompresi Daubechies 2 p koeficientů – p nulových momentů Hladkost lepší rekonstrukce

• Biortogonální wavelety -Haar jediná kompaktní, ortogonální a symetrická -oslabení ortogonality • Reálné x komplexní wavelety • Ortogonální x biortogonální x neortogonální • Jiné typy diskretizace, nedyadické, m-bands

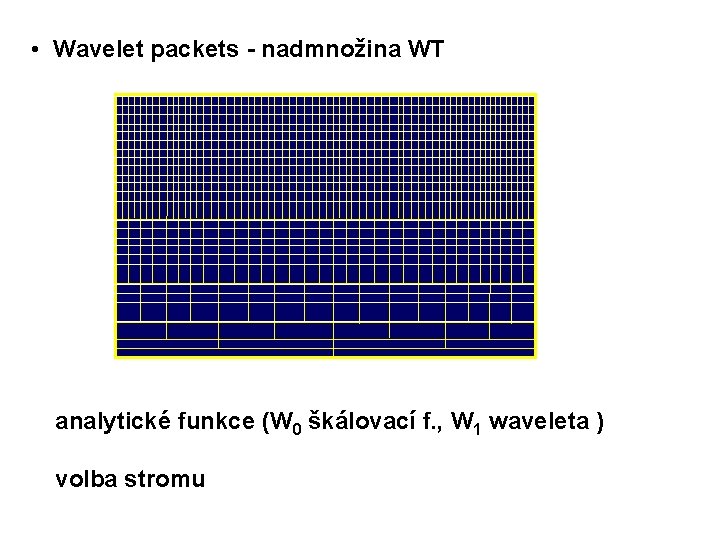
• Wavelet packets - nadmnožina WT analytické funkce (W 0 škálovací f. , W 1 waveleta ) volba stromu (snižování entropie)