Numerikus mdszerek Gyakorlat 10 ht Nemlineris egyenletek megoldsnak

Numerikus módszerek Gyakorlat – 10. hét Nemlineáris egyenletek megoldásának közelítése: intervallumfelező módszer, Newton-módszer és fixpont iteráció Készítette: dr. Nagy Noémi

Nemlineáris egyenletek megoldásának közelítése

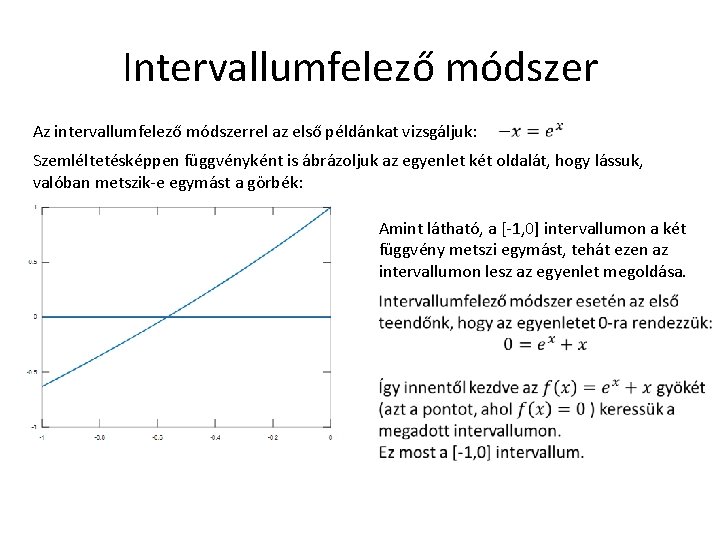
Intervallumfelező módszer Az intervallumfelező módszerrel az első példánkat vizsgáljuk: Szemléltetésképpen függvényként is ábrázoljuk az egyenlet két oldalát, hogy lássuk, valóban metszik-e egymást a görbék: Amint látható, a [-1, 0] intervallumon a két függvény metszi egymást, tehát ezen az intervallumon lesz az egyenlet megoldása.

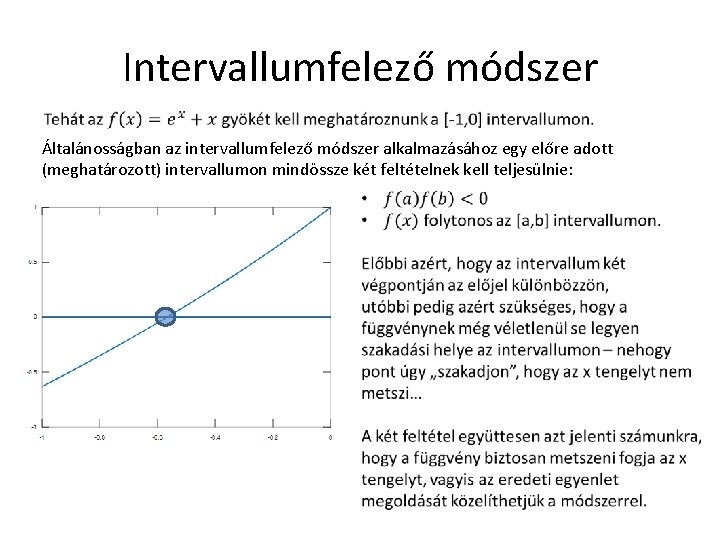
Intervallumfelező módszer Általánosságban az intervallumfelező módszer alkalmazásához egy előre adott (meghatározott) intervallumon mindössze két feltételnek kell teljesülnie:

Intervallumfelező módszer A feltételek teljesülésének ellenőrzése a következő lépés. Ehhez behelyettesítjük az intervallum alsó és felső végpontját:

Intervallumfelező módszer Amennyiben előre megadott hibánál pontosabb közelítést szeretnénk, meg tudjuk határozni, hány lépésre lesz szükségünk:

Intervallumfelező módszer n=5 Amennyiben lépésbenelőre a hibamegadott már 0. 05 hibánál alatt lesz pontosabb közelítést szeretnénk, meg tudjuk határozni, hány lépésre lesz szükségünk:

Intervallumfelező módszer n=5 lépésben a hiba már 0. 05 alatt lesz Az intervallumfelező módszert a legegyszerűbb táblázatos formában összefoglalni: + n ak bk xk=(ak-bk)/2 f(xk) ε=(bk-ak)/2 1 -1 0 - 0. 5 0. 1065 > 0 0. 5 2 -1 - 0. 5 - 0. 75 - 0. 2776 < 0 0. 25 3 - 0. 75 - 0. 625 - 0. 0897 < 0 0. 125 4 - 0. 625 - 0. 5625 0. 0073 > 0 0. 0625 5 - 0. 625 - 0. 59375 0. 03125 AVégül n Meghatározzuk Kiszámoljuk táblázat a algoritmust lépések az fölé száma aktuális a érdemes hibát, a intervallum felezőpontban mint intervallum odaírni, azfelezőpontját. intervallum hogy alsó a függvény az és alsó felső hosszának ésvégpontja felsőfelét. végpontban eredetileg milyen előjelű Nyilvánvalóan az másik végpontja nem változik. el kell döntenünk, az intervallum hogy a utolsó felezőpont azértékét. intervallum alsó vagy felső végpontja lesz: Az így folytatjuk az sor eléréséig: itt ugyanis elegendő a felezőpont volt a függvény értéke, a közelítések soránhogy nemaz fog változni. Ameghatározása. felezőpontban felvetthiszen érték ez előjele megmutatja, első lépésben a pozitív oszlopba kell írnunk a felezőpontot. Amint látjuk, a hiba már 0. 05 alatt van, a felezőpont pedig a pontos megoldásnak így már jó közelítése.

Newton-módszer

Newton-módszer Mielőtt azonban továbbhaladnánk, nézzük meg az algoritmus működését és a feltételek létjogosultságának hátterét: Ez a következőképpen írható le: Ábrázoljuk a feltételeknek megfelelő függvényt és az x 0 pontban érintőt húzunk. Ahol ez metszi az x tengelyt, az lesz a következő közelítés. Ezt ismételjük előre adott lépésszámig vagy amíg a hiba egy adott érték alá nem csökken. x 2 x 1 x 0

Newton-módszer f’(x)=0 f’’(x)=0 f’(x)=0 Mivel ilyen előfordul, kicsit szűkítünk az intervallumon

Newton-módszer xϵ[1, 1. 5] Ezen az intervallumon már az első és második derivált sem veszi fel a 0 értéket.

Newton-módszer A harmadik feltétel továbbra is azt jelenti, hogy az intervallum két végpontjában különbözik az előjel. Figyelni kell rá, hogy radiánban számoljunk!!! xϵ[1, 1. 5]

Newton-módszer A harmadik feltétel továbbra is azt jelenti, hogy az intervallum két végpontjában különbözik az előjel. Figyelni kell rá, hogy radiánban számoljunk!!! xϵ[1, 1. 5]

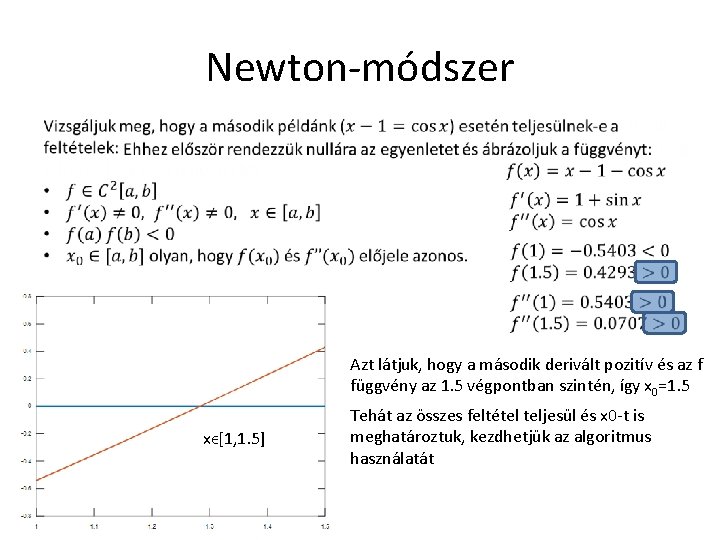
Newton-módszer Azt látjuk, hogy a második derivált pozitív és az f függvény az 1. 5 végpontban szintén, így x 0=1. 5 xϵ[1, 1. 5] Tehát az összes feltétel teljesül és x 0 -t is meghatároztuk, kezdhetjük az algoritmus használatát

Newton-módszer xϵ[1, 1. 5] x 0=1. 5 Azt látjuk, hogy a második derivált pozitív és az f függvény az 1. 5 végpontban szintén, így x 0=1. 5 xϵ[1, 1. 5]

Newton-módszer xϵ[1, 1. 5] x 0=1. 5 Amint látható, a harmadik és negyedik közelítés már ugyanazt az értéket adja nyolc tizedesjegy pontossággal, de azért számoljuk ki a közelítés hibáját a különböző lépésekben.

Newton-módszer xϵ[1, 1. 5] x 0=1. 5

Newton-módszer xϵ[1, 1. 5] x 0=1. 5 Első lépésként alsó-, illetve felsőkorlátot kell adnunk az első és második deriváltra az intervallumon: A sin x függvény az [1, 1. 5] intervallumon pozitív és monoton növekvő, így alsó korlátja az alsó végpontban, azaz 1 -ben lesz, ezért m=f’(1)=1+sin 1=1. 8415 A cos x függvény az [1, 1. 5] intervallumon pozitív és csökkenő, ezért felső korlátja az alsó végpontban, azaz 1 -ben lesz, ezért M=f’’(1)=cos(1)=0. 5430

Newton-módszer xϵ[1, 1. 5] x 0=1. 5 Első lépésként alsó-, illetve felsőkorlátot kell adnunk m=f’(1)=1+sin 1=1. 8415 az. M=f’’(1)=cos(1)=0. 5430 első és második deriváltra az intervallumon: A sin x függvény az [1, 1. 5] intervallumon pozitív és monoton növekvő, így alsó korlátja az alsó végpontban, azaz 1 -ben lesz, ezért m=f’(1)=1+sin 1=1. 8415 A cos x függvény az [1, 1. 5] intervallumon pozitív és csökkenő, ezért felső korlátja az alsó végpontban, azaz 1 -ben lesz, ezért M=f’’(1)=cos(1)=0. 5430

Newton-módszer xϵ[1, 1. 5] x 0=1. 5 m=f’(1)=1+sin 1=1. 8415 M=f’’(1)=cos(1)=0. 5430

Newton-módszer gyökkeresésre x 6=11. 2725 x 7=9. 0185 x 8=7. 2161 x 9=5. 7761 x 10=4. 6286 …

Fixpont iterációs eljárás

Fixpont iterációs eljárás • g folytonos az [a, b] intervallumon • ha xϵ[a, b], akkor a g(x)ϵ[a, b] feltételnek is teljesülnie kell • |g’(x)|<1, ha xϵ[a, b]

Fixpont iterációs eljárás • g folytonos az [a, b] intervallumon • ha xϵ[a, b], akkor a g(x)ϵ[a, b] feltételnek is teljesülnie kell • |g’(x)|<1, ha xϵ[a, b] Elsőként ábrázoljuk az egyenlet két oldalát, hogy tudjuk, mely intervallumon érdemes a megoldást keresni: Amint látjuk, a két függvény metszéspontja valahol 3 és 5 között van, ezért az egyenletet a [3, 5] intervallumon vizsgáljuk. (az intervallum az ilyen típusú feladatok esetén a számonkérés során meg lesz adva)

Fixpont iterációs eljárás • g folytonos az [a, b] intervallumon • ha xϵ[a, b], akkor a g(x)ϵ[a, b] feltételnek is teljesülnie kell • |g’(x)|<1, ha xϵ[a, b] Az egyenlet többféle módon is átírható. Tehát g(x)=(ln x)4. Ez folytonos, tehát az első feltétel teljesül. xϵ[3, 5] Sajnos egyik érték sem esik a [3, 5] intervallumba, így tovább kell keresnünk a g(x) függvényt. A második feltétel ellenőrzéséhez felhasználjuk, hogy a logaritmus függvény monoton növekvő, vagyis a negyedik hatványa is az. Így elég a [3, 5] intervallum alsó és felső végpontját helyettesíteni a függvénybe ahhoz, hogy a feltétel teljesülését ellenőrizzük: g(3)=(ln 3)4 = 1. 4567 g(5)=(ln 5)4 = 6. 7096

Fixpont iterációs eljárás • g folytonos az [a, b] intervallumon • ha xϵ[a, b], akkor a g(x)ϵ[a, b] feltételnek is teljesülnie kell • |g’(x)|<1, ha xϵ[a, b] Az egyenlet többféle módon is átírható. xϵ[3, 5] Mind a két érték 3 és 5 között van, vizsgálhatjuk a harmadik feltételt …

Fixpont iterációs eljárás • g folytonos az [a, b] intervallumon • ha xϵ[a, b], akkor a g(x)ϵ[a, b] feltételnek is teljesülnie kell • |g’(x)|<1, ha xϵ[a, b] xϵ[3, 5]

Fixpont iterációs eljárás • g folytonos az [a, b] intervallumon • ha xϵ[a, b], akkor a g(x)ϵ[a, b] feltételnek is teljesülnie kell • |g’(x)|<1, ha xϵ[a, b] xϵ[3, 5] A harmadik feltétel teljesülésének ellenőrzéséhez ki kell számolnunk a g(x) függvény deriváltját: Bár számolással is ellenőrizhetnénk (mon. növekvő és mon. csökkenő függvény szorzata hogyan viselkedik, stb. ), inkább ábrázoljuk g’(x) függvény abszolútértékét a [3, 5] intervallumon: Azt látjuk, hogy a függvény értéke végig 1 alatt marad, tehát megtaláltuk a feltételeknek eleget tevő g(x) függvényt

Fixpont iterációs eljárás xϵ[3, 5]

Fixpont iterációs eljárás xϵ[3, 5] Továbbá legyen x 0=3 (az intervallum alsó végpontja) – ezt, ha nincs megadva, mi választhatjuk meg.

Fixpont iterációs eljárás xϵ[3, 5] x 0=3 Továbbá legyen x 0=3 (az intervallum alsó végpontja) – ezt, ha nincs megadva, mi választhatjuk meg. q=0. 45

Fixpont iterációs eljárás xϵ[3, 5] x 0=3 q=0. 45 Az algoritmust addig folytatjuk, amíg a hibánk valami előre megadott érték alá nem csökken. Például ha 0. 1 -et adtunk volna meg mint hibakorlát, elegendő lett volna a harmadik közelítést meghatározni.

Fixpont iterációs eljárás működése xϵ[3, 5] x 0=3 Az x=g(x) egyenlet megoldását szeretnénk megkapni, vagyis a kékkel és pirossal jelzett görbék metszetét. Ehhez mindössze annyit kell tennünk, hogy „cikázunk” a két görbe között. (feltéve, hogy a g(x) teljesíti a korábban leírt feltételeket) x 0=3 x 1 x 2 x 3. . .

Nemlineáris egyenlet megoldásának közelítése MATLAB-ban Nyilván érdemes a 2. sorok végére a pontosvesszőt kirakni, valamint nem elfeledkezni róla, hogy ha pl. a függvényben negyedik gyök szerepel (mint a fixpont iterációnál látott példában), néhány művelet előtt a. (pont) kihelyezendő: Most, hogy a függvényeinket megtanítottuk, nézzük a különböző módszerekre írható függvényeket.

Intervallumfelező módszer MATLAB-ban A 9. sorban mindössze az aktuális hibát határozzuk meg – egyfajta önellenőrzésként A 10. sorban pedig kiszámoljuk az új intervallum felezőpontját és folytatjuk az algoritmust, amíg az n-edik lépésig jutunk. A 4. sorban feltűnhetett, hogy a for ciklus 2 -től indul. Ennek magyarázata mindössze, hogy a harmadik sorban már kiszámoltuk az első közelítést.

Newton-módszer MATLAB-ban Amint látható, nem bonyolítottuk túl a Newton-módszerre írt függvényt: A függvény első paramétere az x 0 kiindulópont, aminek meghatározását korábban láttunk, valamint n a lépésszámot jelenti. A függvény 2 -5 sorában a Newton-módszer algoritmusa látszik. Ne felejtsük el, hogy a Newton-módszer használata előtt a függvényt (f) és deriváltját (fd) definiálnunk (vagy szükség esetén módosítanunk) kell. Ahogy arról sem, hogy a Newton-módszer alkalmazása előtt érdemes a feltételek teljesülését ellenőrizni.

Fixpont iterációs eljárás MATLAB-ban