Nesterovs excessive gap technique and poker Andrew Gilpin





![(Un)scalability of LP solvers • Rhode Island poker [Shi & Littman 01] – LP (Un)scalability of LP solvers • Rhode Island poker [Shi & Littman 01] – LP](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-7.jpg)





![Nesterov’s main theorem Theorem [Nesterov 05] There exists an algorithm such that after at Nesterov’s main theorem Theorem [Nesterov 05] There exists an algorithm such that after at](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-13.jpg)



![From the simplex to the complex Theorem [Hoda, G. , Peña 06] A nice From the simplex to the complex Theorem [Hoda, G. , Peña 06] A nice](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-17.jpg)

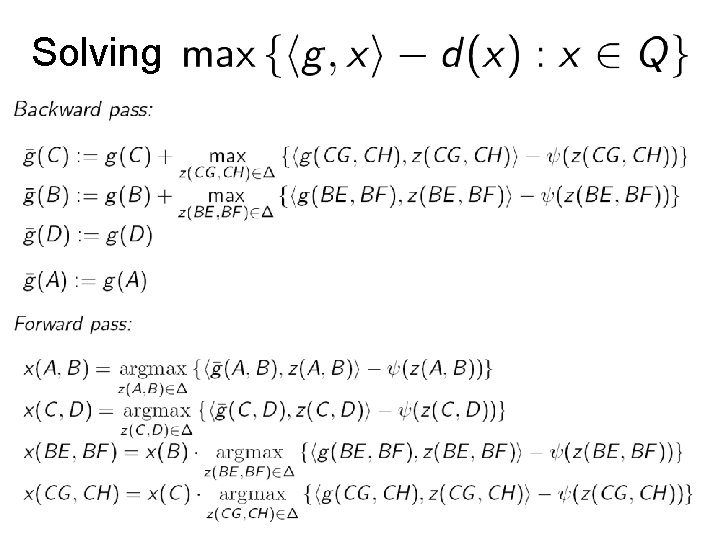

![Heuristics [G. , Hoda, Peña, Sandholm 07] • Heuristic 1: Aggressive μ reduction – Heuristics [G. , Hoda, Peña, Sandholm 07] • Heuristic 1: Aggressive μ reduction –](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-21.jpg)
![Matrix-vector multiplication in poker [G. , Hoda, Peña, Sandholm 07] • The main time Matrix-vector multiplication in poker [G. , Hoda, Peña, Sandholm 07] • The main time](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-22.jpg)

![Potential-aware automated abstraction [G. , Sandholm, Sørensen 07] • Most prior automated abstraction algorithms Potential-aware automated abstraction [G. , Sandholm, Sørensen 07] • Most prior automated abstraction algorithms](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-25.jpg)

![[G. , Sandholm, Sørensen 07] [G. , Sandholm, Sørensen 07]](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-27.jpg)
![[G. , Sandholm, Sørensen 07] [G. , Sandholm, Sørensen 07]](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-28.jpg)
![[G. , Sandholm, Sørensen 07] [G. , Sandholm, Sørensen 07]](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-29.jpg)


- Slides: 31

Nesterov’s excessive gap technique and poker Andrew Gilpin CMU Theory Lunch Feb 28, 2007 Joint work with: Samid Hoda, Javier Peña, Troels Sørensen, Tuomas Sandholm

Outline • • • Two-person zero-sum sequential games First-order methods for convex optimization Nesterov’s excessive gap technique (EGT) EGT for sequential games Heuristics for EGT Application to Texas Hold’em poker

We want to solve: If Q 1 and Q 2 are simplices, complexes, this is the Nash equilibrium problem for two-person zero-sum matrix games sequential games

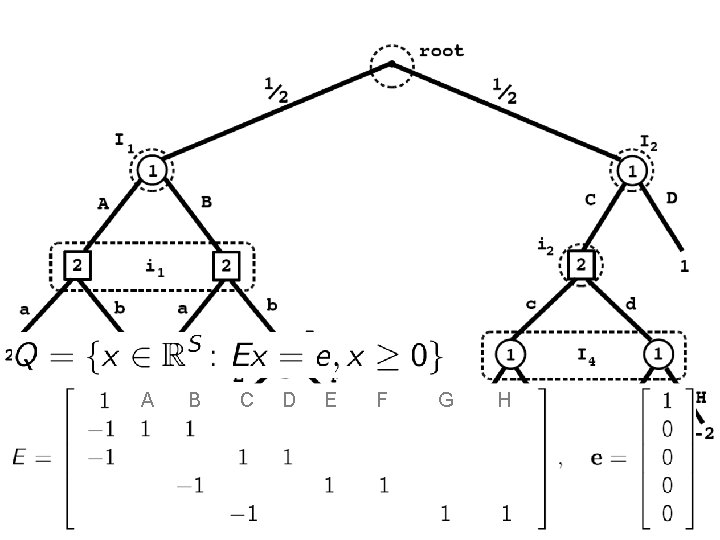
What’s a complex? It’s just like a simplex, but more complex. Each player’s complex encodes her set of realization plans in the game In particular, player 1’s complex is where E and e depend on the game…

A B C D E F G H

Recall our problem: where Q 1 and Q 2 are complexes Since Q 1 and Q 2 have a linear description, this problem can be solved as an LP. However, current LP solution methods do not scale
![Unscalability of LP solvers Rhode Island poker Shi Littman 01 LP (Un)scalability of LP solvers • Rhode Island poker [Shi & Littman 01] – LP](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-7.jpg)
(Un)scalability of LP solvers • Rhode Island poker [Shi & Littman 01] – LP has 91 million rows and columns – Applying Game. Shrink automated abstraction algorithm yields an LP with only 1. 2 million rows and columns, and 50 million nonzeros [G. & Sandholm, 06 a] – Solution requires 25 GB RAM and over a week of CPU time • Texas Hold’em poker – ~1018 nodes in game tree – Lossy abstractions need to be performed – Limitations of current solver technology primary limitation to achieving expert-level strategies [G. & Sandholm 06 b, 07 a] • Instead of standard LP solvers, what about a first-order method?

Convex optimization Suppose we want to solve where f is convex. Note that this formulation captures ALL convex optimization problems (can model feasible space using an indicator function) For general f, convergence Analysis based requires on black-box O(1/ε 2) iterations oracle (e. g. , for subgradient accessmethods) model. Can we do better by looking inside the box? For smooth, strongly convex f with Lipschitzcontinuous gradient, can be done in O(1/ε½) iterations

Strong convexity A function if there exists for all is strongly convex such that and all is the strong convexity parameter of d

Recall our problem: where Q 1 and Q 2 are complexes Equivalently: where and

, , Unfortunately, Φ and f are non-smooth Fortunately, they have a special structure Let d 1, d 2 be smooth and strongly convex on Q 1, Q 2 These are called prox-functions Now let μ > 0 and consider: These are well-defined smooth functions

Excessive gap condition From weak duality, we have that f(y) ≤ Φ(x) The excessive gap condition requires that fμ(y) ≤ Φμ(x) (EGC) The algorithm maintains (EGC), and gradually decreases μ As μ decreases, the smoothed functions approach the non-smooth functions, and thus iterates satisfying (EGC) converge to optimal solutions
![Nesterovs main theorem Theorem Nesterov 05 There exists an algorithm such that after at Nesterov’s main theorem Theorem [Nesterov 05] There exists an algorithm such that after at](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-13.jpg)
Nesterov’s main theorem Theorem [Nesterov 05] There exists an algorithm such that after at most N iterations, the iterates have duality gap at most Furthermore, each iteration only requires solving three problems of the form and performing three matrix-vector product operations on A.

Nice prox functions A prox function d for Q is nice if it is: 1. Strongly convex continuous everywhere in Q, and differentiable in the relative interior of Q 2. The min of d over Q is 0 3. The following maps are easily computable:

Nice simplex prox function 1: Entropy

Nice simplex prox function 2: Euclidean sargmax can be computed in O(n log n) time
![From the simplex to the complex Theorem Hoda G Peña 06 A nice From the simplex to the complex Theorem [Hoda, G. , Peña 06] A nice](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-17.jpg)
From the simplex to the complex Theorem [Hoda, G. , Peña 06] A nice prox function can be constructed for the complex via a recursive application of any nice prox function for the simplex

Prox function example Let be any nice simplex prox function. The prox function for this matrix is:
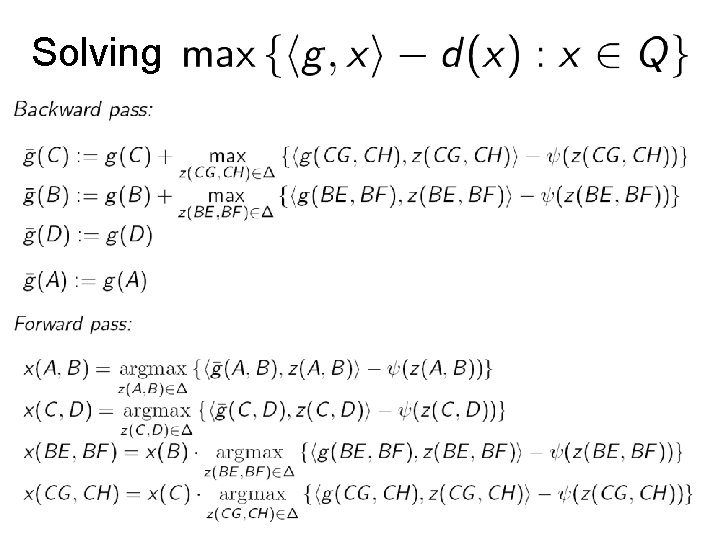
Solving

(similar to b(i-vii))
![Heuristics G Hoda Peña Sandholm 07 Heuristic 1 Aggressive μ reduction Heuristics [G. , Hoda, Peña, Sandholm 07] • Heuristic 1: Aggressive μ reduction –](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-21.jpg)
Heuristics [G. , Hoda, Peña, Sandholm 07] • Heuristic 1: Aggressive μ reduction – The μ given in the previous algorithm is a conservative choice guaranteeing convergence – In practice, we can do much better by aggressively pushing μ, while checking that the excessive gap condition is satisfied • Heuristic 2: Balanced μ reduction – To prevent one μ from dominating the other, we also perform periodic adjustments to keep them within a small factor of one another
![Matrixvector multiplication in poker G Hoda Peña Sandholm 07 The main time Matrix-vector multiplication in poker [G. , Hoda, Peña, Sandholm 07] • The main time](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-22.jpg)
Matrix-vector multiplication in poker [G. , Hoda, Peña, Sandholm 07] • The main time and space bottleneck of the algorithm is the matrix-vector product on A • Instead of storing the entire matrix, we can represent it as a composition of Kronecker products • We can also effectively take advantage of parallelization in the matrix-vector product to achieve near-linear speedup

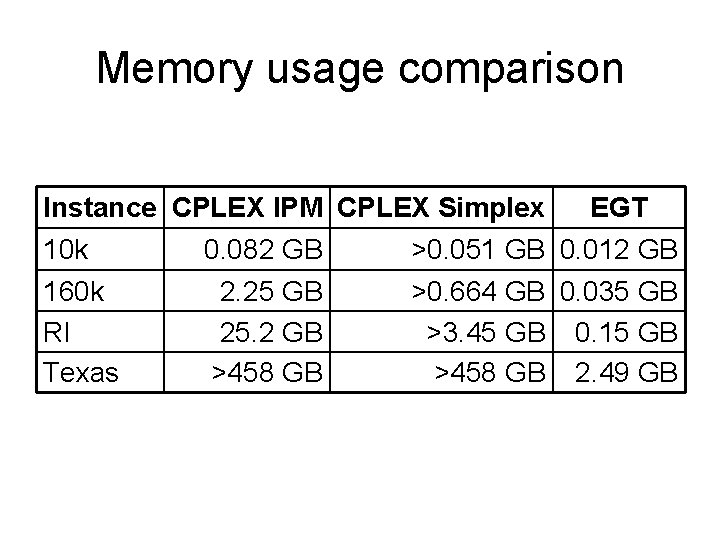
Memory usage comparison Instance CPLEX IPM CPLEX Simplex EGT 10 k 0. 082 GB >0. 051 GB 0. 012 GB 160 k 2. 25 GB >0. 664 GB 0. 035 GB RI 25. 2 GB >3. 45 GB 0. 15 GB Texas >458 GB 2. 49 GB

Poker • Poker is a recognized challenge problem in AI because (among other reasons) – the other players’ cards are hidden; – bluffing and other deceptive strategies are needed in a good player; – there is uncertainty about future events. • Texas Hold’em: most popular variant of poker • Two-player game tree has ~1018 nodes
![Potentialaware automated abstraction G Sandholm Sørensen 07 Most prior automated abstraction algorithms Potential-aware automated abstraction [G. , Sandholm, Sørensen 07] • Most prior automated abstraction algorithms](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-25.jpg)
Potential-aware automated abstraction [G. , Sandholm, Sørensen 07] • Most prior automated abstraction algorithms employ a myopic expected value computation as a similarity metric – This ignores hands like flush draws where although the probability of winning is small, the payoff could be high • Our newest algorithm considers higher-dimensional spaces consisting of histograms over abstracted classes of states from later stages of the game • This enables our bottom-up abstraction algorithm to automatically take into account positive and negative potential

Solving the four-round model • Computed abstraction with – 20 first-round buckets – 800 second-round buckets – 4800 third-round buckets – 28800 fourth-round buckets • Algorithm using 30 GB RAM – Simply representing as an LP requires 32 TB – Outputs new, improved solution every 2. 5 days
![G Sandholm Sørensen 07 [G. , Sandholm, Sørensen 07]](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-27.jpg)
[G. , Sandholm, Sørensen 07]
![G Sandholm Sørensen 07 [G. , Sandholm, Sørensen 07]](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-28.jpg)
[G. , Sandholm, Sørensen 07]
![G Sandholm Sørensen 07 [G. , Sandholm, Sørensen 07]](https://slidetodoc.com/presentation_image_h/d2aa3e3654801a0ba757fb4e59ad8993/image-29.jpg)
[G. , Sandholm, Sørensen 07]

Future research • Customizing second-order (e. g. interiorpoint methods) for the equilibrium problem • Additional heuristics for improving practical performance of EGT algorithm • Techniques for finding an optimal solution from an ε-solution

Thank you ☺
 Tim gilpin
Tim gilpin Gap poker
Gap poker Bogʻlovchisiz qoʻshma gaplarga misollar
Bogʻlovchisiz qoʻshma gaplarga misollar Compiler bridges the semantic gap between which domains?
Compiler bridges the semantic gap between which domains? Penyebab penyakit benign neoplasm of breast d24
Penyebab penyakit benign neoplasm of breast d24 Chapter 15 furniture styles and construction answer key
Chapter 15 furniture styles and construction answer key Extent of researcher interference
Extent of researcher interference Grid radius radiology
Grid radius radiology Air gap technique in radiology
Air gap technique in radiology Excessive concavity welding
Excessive concavity welding Excessive acid production
Excessive acid production Anorexia and stomach ulcers
Anorexia and stomach ulcers Take away any liquid near your working area true or false
Take away any liquid near your working area true or false Nutrition care plan
Nutrition care plan Dumping syndrome pathophysiology
Dumping syndrome pathophysiology Pathophysiology of peptic ulcer
Pathophysiology of peptic ulcer Excessive belching cancer
Excessive belching cancer Excessive drinking by county
Excessive drinking by county Pes statement for obesity
Pes statement for obesity Excessive subordination
Excessive subordination Cryptinject
Cryptinject Excessive bending
Excessive bending Organic nitrogen sources
Organic nitrogen sources Posterior palatal seal slideshare
Posterior palatal seal slideshare Alimentation excessive
Alimentation excessive Excessive military spending in rome
Excessive military spending in rome Eighth amendment excessive bail
Eighth amendment excessive bail Criminal justice lesson
Criminal justice lesson 8 amendment
8 amendment Excessive grant sql server
Excessive grant sql server Scopy a suffix denoting a visual examination
Scopy a suffix denoting a visual examination Three schools of bargaining ethics
Three schools of bargaining ethics