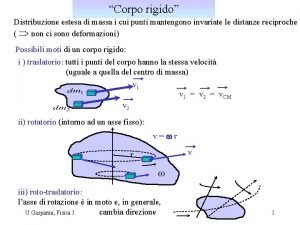
Moto di rotazione di un corpo rigido intorno

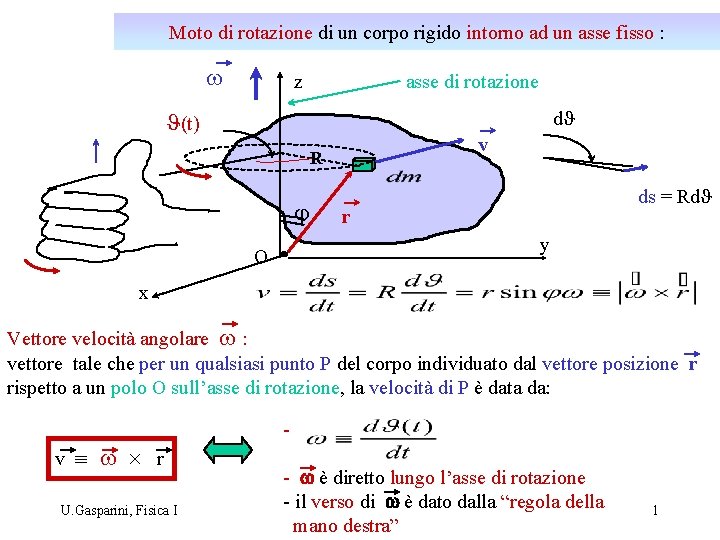
Moto di rotazione di un corpo rigido intorno ad un asse fisso : w z asse di rotazione J(t) d. J v R j ds = Rd. J r y O x Vettore velocità angolare w : vettore tale che per un qualsiasi punto P del corpo individuato dal vettore posizione r rispetto a un polo O sull’asse di rotazione, la velocità di P è data da: v º w ´ r U. Gasparini, Fisica I - w è diretto lungo l’asse di rotazione - il verso di w è dato dalla “regola della mano destra” 1

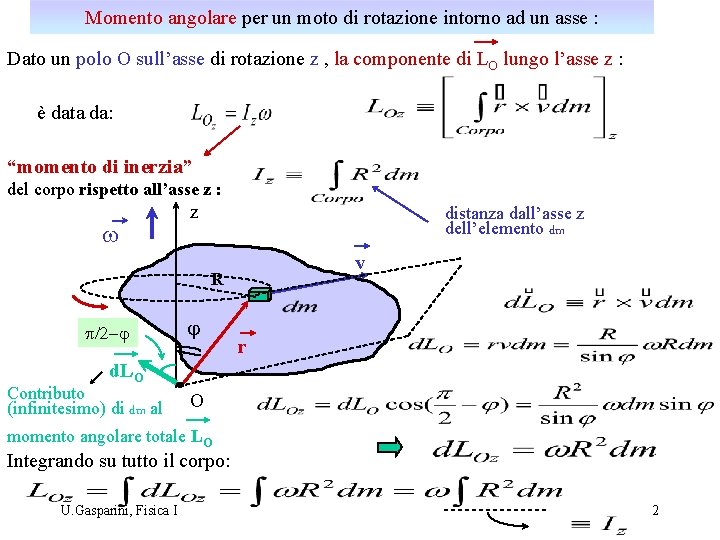
Momento angolare per un moto di rotazione intorno ad un asse : Dato un polo O sull’asse di rotazione z , la componente di LO lungo l’asse z : è data da: “momento di inerzia” del corpo rispetto all’asse z : w z distanza dall’asse z dell’elemento dm v R p/2 -j j r d. LO Contributo (infinitesimo) di dm al O momento angolare totale LO Integrando su tutto il corpo: U. Gasparini, Fisica I 2

Momento di inerzia Dimensioni del momento d’inerzia: Il momento d’inerzia dipende dalla forma geometrica del corpo, dalla sua distribuzione di massa (densità) e dall’asse considerato; non è una proprietà intrinseca del corpo Esempio: momento d’inerzia di un asta omogenea di lunghezza e massa M: i) rispetto ad un asse perpendicolare passante per un suo estremo : z dm R densità lineare ii) rispetto ad un asse perpendicolare passante per il suo centro di massa : z G R dm x x

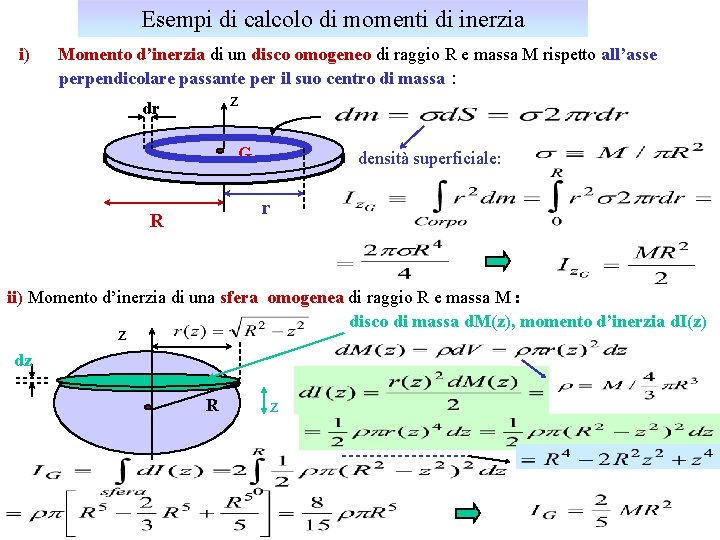
Esempi di calcolo di momenti di inerzia i) Momento d’inerzia di un disco omogeneo di raggio R e massa M rispetto all’asse perpendicolare passante per il suo centro di massa : z dr G densità superficiale: r R ii) Momento d’inerzia di una sfera omogenea di raggio R e massa M : disco di massa d. M(z), momento d’inerzia d. I(z) z dz R z

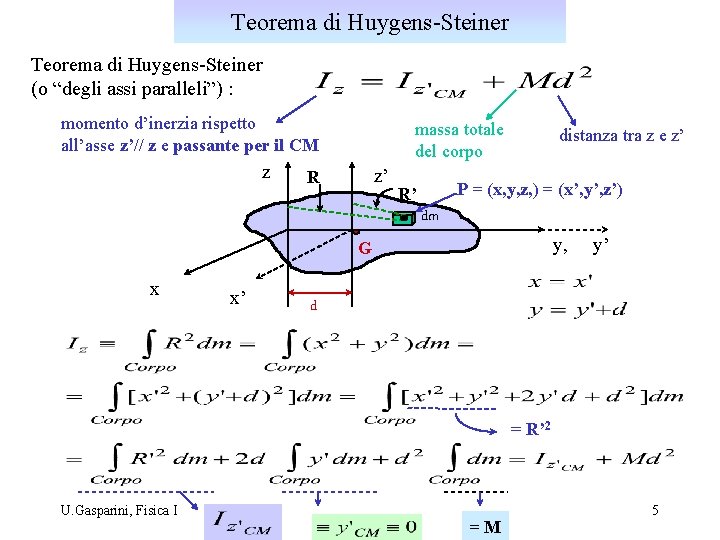
Teorema di Huygens-Steiner (o “degli assi paralleli”) : momento d’inerzia rispetto all’asse z’// z e passante per il CM z massa totale del corpo z’ R distanza tra z e z’ P = (x, y, z, ) = (x’, y’, z’) R’ dm y, G x x’ y’ d = R’ 2 U. Gasparini, Fisica I =M 5

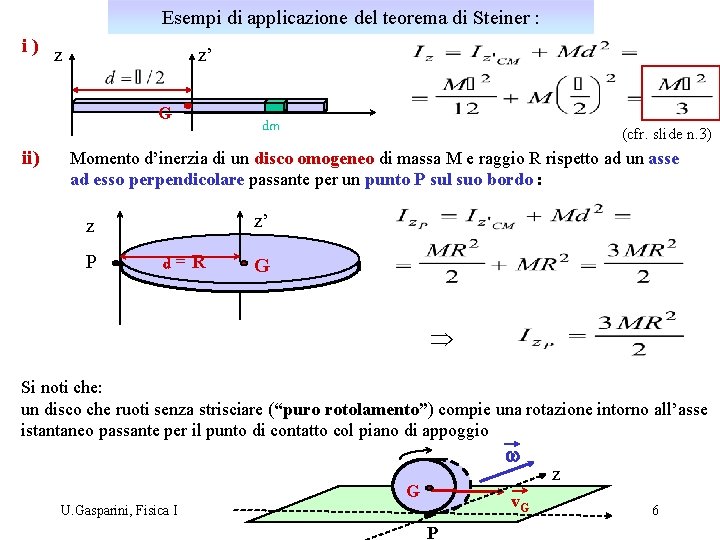
Esempi di applicazione del teorema di Steiner : i) z z’ G ii) dm (cfr. slide n. 3) Momento d’inerzia di un disco omogeneo di massa M e raggio R rispetto ad un asse ad esso perpendicolare passante per un punto P sul suo bordo : z’ z P d=R G Þ Si noti che: un disco che ruoti senza strisciare (“puro rotolamento”) compie una rotazione intorno all’asse istantaneo passante per il punto di contatto col piano di appoggio w G v. G U. Gasparini, Fisica I P z 6

Teorema del momento angolare per un corpo rigido Il teorema del momento angolare ( “ 2 a equazione cardinale” della dinamica): massa totale del sistema momento totale delle forze esterne rispetto al polo O velocità del polo O nel sistema di riferimento inerziale nel quale i Punti materiale hanno le velocità v che entrano nella definizione di LO : per un corpo rigido in rotazione intorno ad un asse fisso z ( v. O= 0) : z w può essere riformulato utilizzando il concetto di momento d’inerzia. Proiettando tale equazione lungo l’asse di rotazione: O ( in formale analogia con la legge di Newton: U. Gasparini, Fisica I ) accelerazione angolare : 7

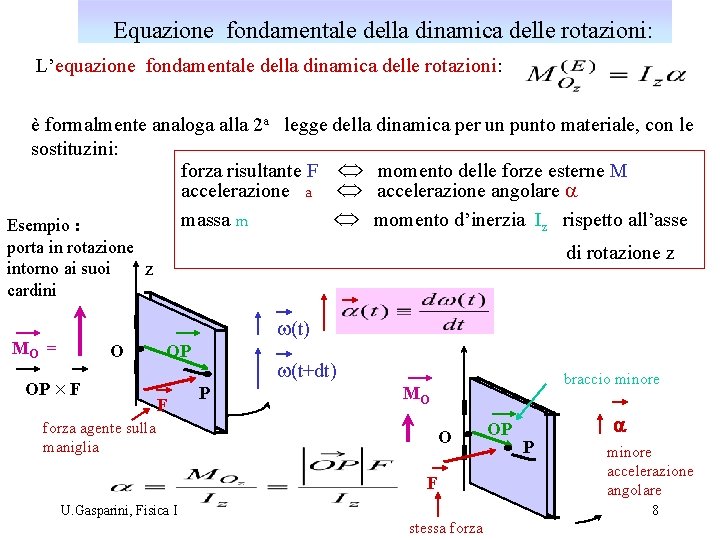
Equazione fondamentale della dinamica delle rotazioni: L’equazione fondamentale della dinamica delle rotazioni: è formalmente analoga alla 2 a legge della dinamica per un punto materiale, con le sostituzini: forza risultante F Û momento delle forze esterne M accelerazione a Û accelerazione angolare a massa m Û momento d’inerzia Iz rispetto all’asse Esempio : porta in rotazione intorno ai suoi z cardini di rotazione z w(t) MO = O OP ´ F OP F forza agente sulla maniglia w(t+dt) P braccio minore MO O F U. Gasparini, Fisica I OP a P minore accelerazione angolare 8 stessa forza

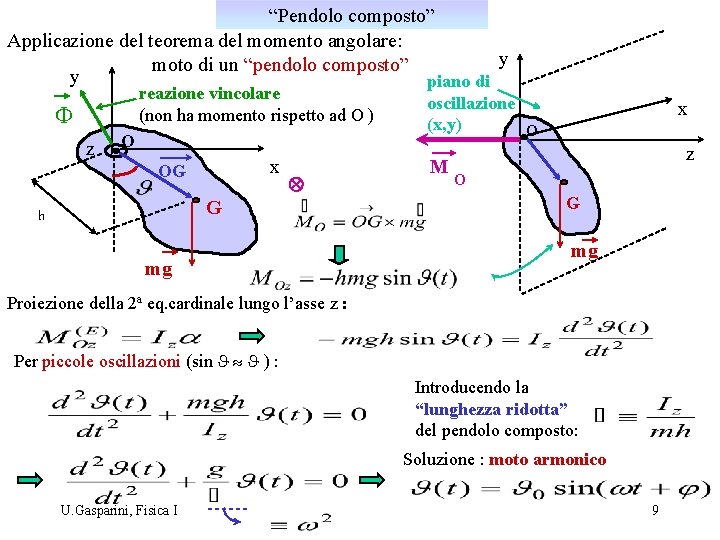
“Pendolo composto” Applicazione del teorema del momento angolare: y moto di un “pendolo composto” y piano di reazione vincolare (non ha momento rispetto ad O ) F z O x OG Ä G h mg oscillazione (x, y) O M x z O G mg Proiezione della 2 a eq. cardinale lungo l’asse z : Per piccole oscillazioni (sin J » J ) : Introducendo la “lunghezza ridotta” del pendolo composto: Soluzione : moto armonico U. Gasparini, Fisica I 9

“Assi reciproci” di un pendolo composto: piano di oscillazione (x, y) y asse di rotazione O “assi reciproci” z h G h’ mg O’ z’ “asse di oscillazione” : asse parallelo all’asse di rotazione, passante per il punto O’ a distanza (º lunghezza ridotta ) dal punto di sospensione O lungo la retta OG I periodi di oscillazione intorno agli assi z e z’ (“assi reciproci”) sono uguali. Infatti: La lunghezza ridotta per le oscillazioni intorno ad O’ è: U. Gasparini, Fisica I

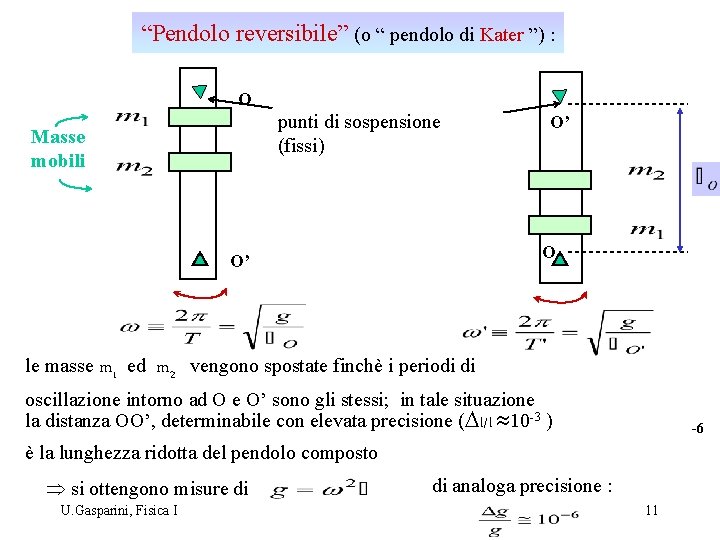
“Pendolo reversibile” (o “ pendolo di Kater ”) : O punti di sospensione (fissi) Masse mobili O O’ le masse m 1 ed O’ m 2 vengono spostate finchè i periodi di oscillazione intorno ad O e O’ sono gli stessi; in tale situazione la distanza OO’, determinabile con elevata precisione (Dl/l » 10 -3 ) -6 è la lunghezza ridotta del pendolo composto Þ si ottengono misure di U. Gasparini, Fisica I di analoga precisione : 11

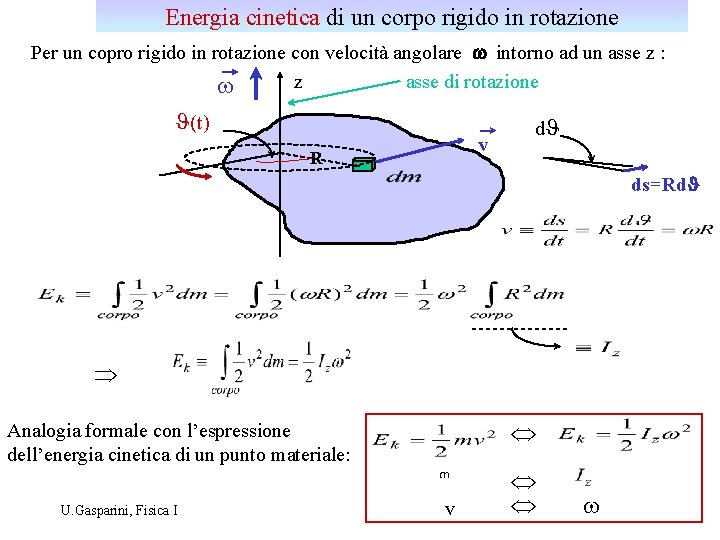
Energia cinetica di un corpo rigido in rotazione Per un copro rigido in rotazione con velocità angolare w intorno ad un asse z : z asse di rotazione w J(t) v R d. J ds=Rd. J Þ Analogia formale con l’espressione dell’energia cinetica di un punto materiale: U. Gasparini, Fisica I Û m v Û Û w

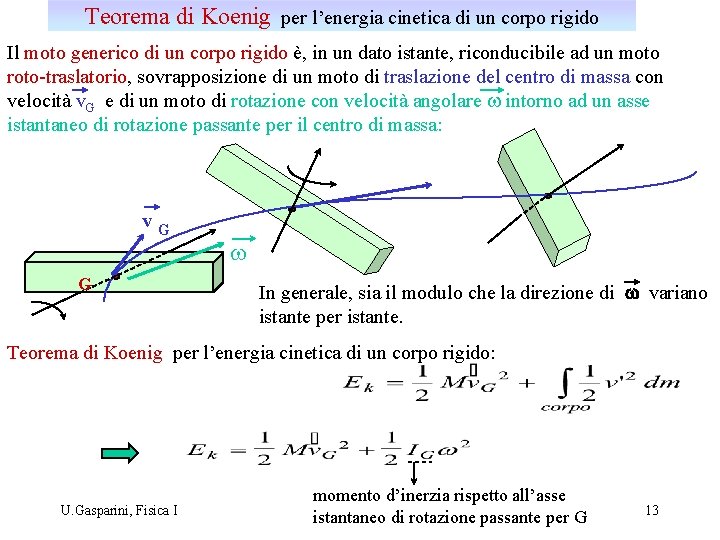
Teorema di Koenig per l’energia cinetica di un corpo rigido Il moto generico di un corpo rigido è, in un dato istante, riconducibile ad un moto roto-traslatorio, sovrapposizione di un moto di traslazione del centro di massa con velocità v. G e di un moto di rotazione con velocità angolare w intorno ad un asse istantaneo di rotazione passante per il centro di massa: v G G w In generale, sia il modulo che la direzione di w variano istante per istante. Teorema di Koenig per l’energia cinetica di un corpo rigido: U. Gasparini, Fisica I momento d’inerzia rispetto all’asse istantaneo di rotazione passante per G 13

Energia cinetica di un copro rigido Il teorema di Koenig per un corpo rigido puo’ essere ricavato dal teorema di Huygens-Steiner : w z z’ d v. G = wd G corpo in rotazione intorno all’asse z t. di Huygens-Steiner U. Gasparini, Fisica I 14

Teorema dell’energia cinetica per un corpo rigido: Per un corpo rigido, il lavoro infinitesimo d. W(I) delle forze interne è nullo: lavoro delle sole forze esterne poichè in un corpo rigido le distanze relative rjk rimangono invariate º 0 U. Gasparini, Fisica I 15