Assi principali di inerzia Per una rotazione intorno

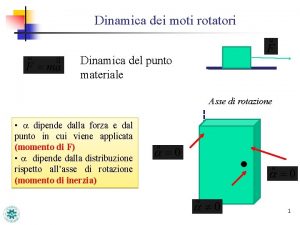
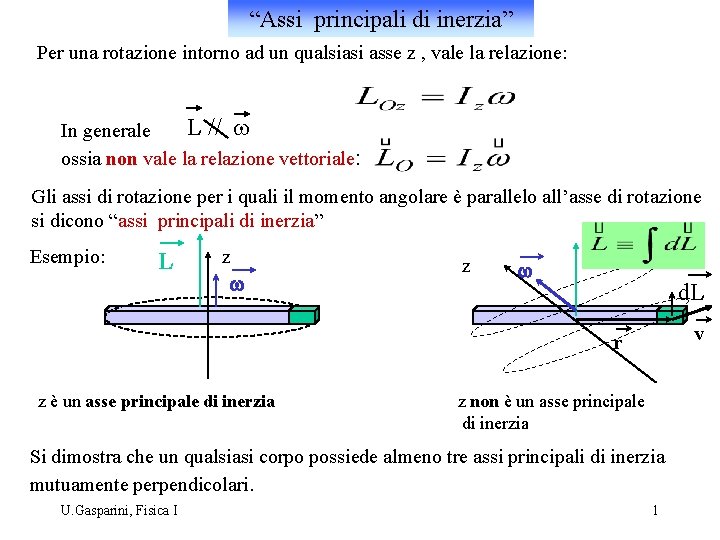
“Assi principali di inerzia” Per una rotazione intorno ad un qualsiasi asse z , vale la relazione: L // w In generale ossia non vale la relazione vettoriale: Gli assi di rotazione per i quali il momento angolare è parallelo all’asse di rotazione si dicono “assi principali di inerzia” Esempio: L z w d. L v r z è un asse principale di inerzia z non è un asse principale di inerzia Si dimostra che un qualsiasi corpo possiede almeno tre assi principali di inerzia mutuamente perpendicolari. U. Gasparini, Fisica I 1

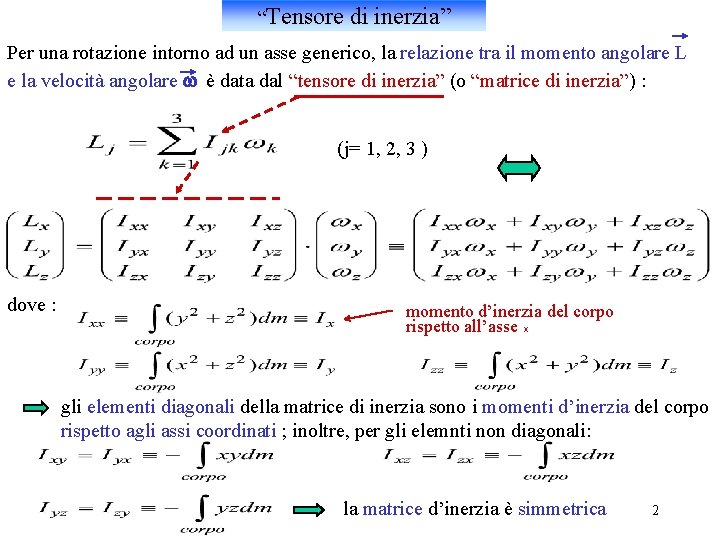
“Tensore di inerzia” Per una rotazione intorno ad un asse generico, la relazione tra il momento angolare L e la velocità angolare w è data dal “tensore di inerzia” (o “matrice di inerzia”) : (j= 1, 2, 3 ) dove : momento d’inerzia del corpo rispetto all’asse x gli elementi diagonali della matrice di inerzia sono i momenti d’inerzia del corpo rispetto agli assi coordinati ; inoltre, per gli elemnti non diagonali: la matrice d’inerzia è simmetrica 2

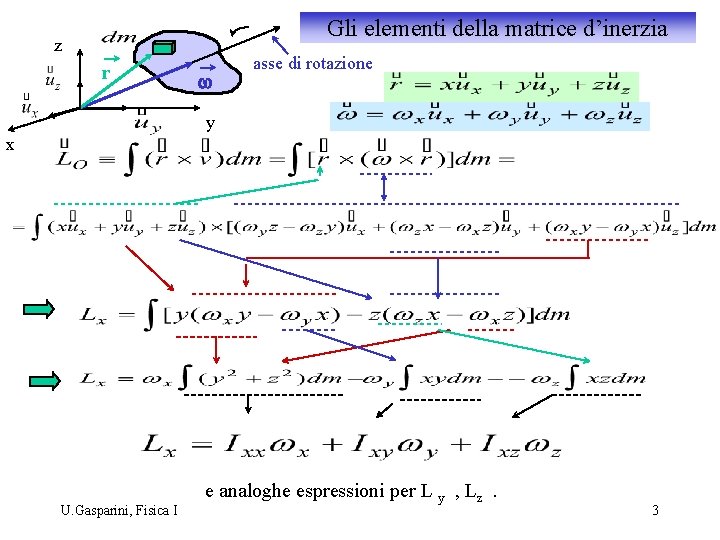
Gli elementi della matrice d’inerzia z r w asse di rotazione y x U. Gasparini, Fisica I e analoghe espressioni per L y , Lz. 3

Momento anolare e matrice d’inerzia Dato un asse di rotazione, è possibile scegliere un’asse coordinato (ad es. l’asse z) lungo la direzione di rotazione; in questo caso: l’espressione per il momento angolare: si semplifica : componente del momento angolare lungo l’asse di rotazione Tuttavia, essendo in generale il momento angolare ha componenti lungo gli assi x, y perpendicolari all’asse di rotazione, ossia L // w. , , l’asse z e’ un asse principale di inerzia. Un sistema di coordinate nel quale la matrice di inerzia è diagonale costituisce un sistema di assi principali di inerzia U. Gasparini, Fisica I 4 Se

Teorema di Poinsot Il momento d’inerzia I z’ rispetto ad un generico asse z’ di rotazione passante per un punto O e individuato dal versore è esprimibile in funzione del tensore di inerzia Ijk : z r O x Ixx Iyy z’ dm R j y Izz 5

“Ellissoide di inerzia” L’equazione che esprime il momento d’inerzia: può essere riscritta, dividendo ambo i membri per : (1) con : la (1) è l’equazione di un ellissoide, detto “ellissoide di inerzia” del corpo rispetto al generico punto O del corpo: essa individua la superficie i cui punti sono a distanza coseni direttori dell’asse z’ dal punto O Il momento d’inerzia rispetto ad un qualsiasi asse z’ passante per un punto O del corpo è individuato dall’intersezione P dell’asse z’ con l’ellissoide d’inerzia del corpo Z mediante la relazione: z’ Ellissoide P d’inerzia O Y (“Teorema di Poinsot”) X U. Gasparini, Fisica I

Ellissoide d’inerzia e assi principali Dato un generico punto O del corpo, la forma ed orientazione nello spazio dell’ellissoide d’inerzia rispetto ad O e’ caratteristica del corpo e non dipende dagli assi coordinati ; solo il valore degli elementi della matrice d’inerzia dipende da questa scelta Z Z’ z’ z’ Ellissoide P P d’inerzia Y O O X’ X equazione dell’ellissoide: , Y’ , … ecc. E’ sempre possibile “diagonalizzare” la matrice d’inerzia, ossia trovare un sistema di assi coordinati per il quale sia: equazione dell’ellissoide: Z X, Y, Z “assi principali d’inerzia”: per rotazioni intorno ad essi: U. Gasparini, Fisica I (j=x, y, z) X 7 Y

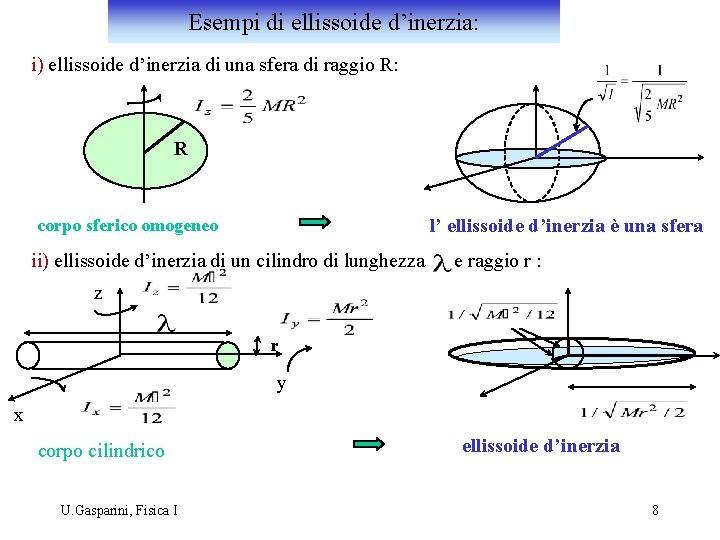
Esempi di ellissoide d’inerzia: i) ellissoide d’inerzia di una sfera di raggio R: R l’ ellissoide d’inerzia è una sfera corpo sferico omogeneo ii) ellissoide d’inerzia di un cilindro di lunghezza e raggio r : z r y x corpo cilindrico U. Gasparini, Fisica I ellissoide d’inerzia 8

Moto di “puro rotolamento” Rototraslazione di un corpo rigido di sezione circolare (disco, cilindro, sfera) su di un piano, per il quale il punto P (o i punti) di contatto tra il corpo ed il piano è fermo rispetto a questo ( Þ non vi è strisciamento ) w y R v. G G z P x Condizione cinematica: velocità del CM velocità relativa di P rispetto al CM Derivando rispetto al tempo: U. Gasparini, Fisica I accelerazione angolare velocità angolare di rotazione 9

Moto di puro rotolamento (II) w y f z G R F a. G x P Se una forza F viene applicata in G, nel punto di contatto P si sviluppa una reazione vincolare f che ha una componente lungo il piano: si ha cioè una forza d’attrito statico perchè si abbia un moto accelerato di puro rotolamento il piano d’appoggio deve essere scabro. Ciò è evidente dalla equazione del momento angolare rispetto al CM : Proiettando lungo l’asse z : è la forza d’attrito statico in P (l’unica che ha un momento rispetto a G) ad essere responsabile dell’accelerazione angolare del sistema richiesta perchè si abbia un moto accelerato di puro rotolamento. U. Gasparini, Fisica I 10

“Attrito volvente” Una forza d’attrito statico che agisce in un unico punto geometrico di contatto tra superfici indeformabili è una schematizzazione; in realtà si ha una deformazione delle superfici di contatto, lungo le quali si sviluppano reazioni vincolari la cui risultante ha una componente lungo la direzione del moto, detta “attrito volvente”: a. CM G f Þ F a. CM x z Dal teorema del moto del CM: proiettando lungo la direzione del moto (asse x ) : ( si noti: Þ ) < 0. U. Gasparini, Fisica I < F/M 11

Esempio: moto di puro rotolamento di un disco omogeneo di raggio R e massa M momento di inerzia rispetto all’asse z passante per G: y w G z R f F a. G P L’accelerazione x a. CM è inferiore a quella che si avrebbe per un punto materiale di massa M soggetto alla stessa forza F. Il lavoro compiuto dalla forza F in un tratto Dx : determina un aumento di energia cinetica sia di traslazione che di rotazione, mentre per un punto materiale: 12

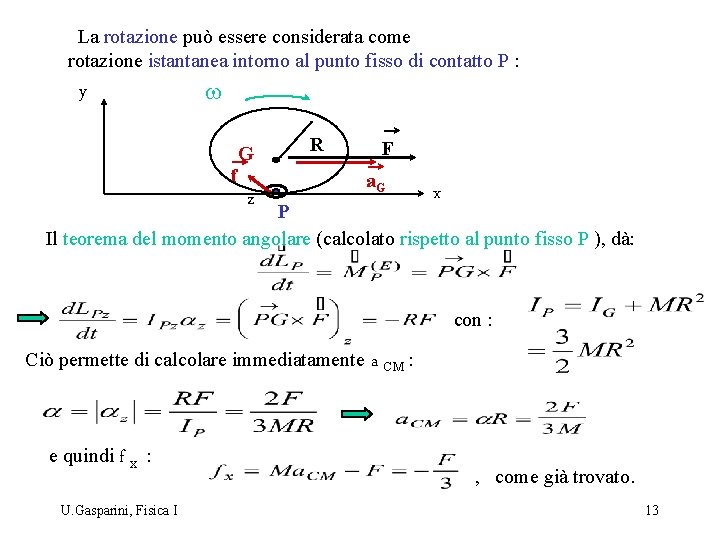
La rotazione può essere considerata come rotazione istantanea intorno al punto fisso di contatto P : y w G R f z F a. G x P Il teorema del momento angolare (calcolato rispetto al punto fisso P ), dà: con : Ciò permette di calcolare immediatamente e quindi f x : U. Gasparini, Fisica I a CM : , come già trovato. 13

Forza d’attrito statico nel puro rotolamento La forza d’attrito statico fx non sempre è opposta al moto; ad esempio, se la forza ‘motrice’ F è applicata nel punto A sulla sommità del disco: y G z F A R f P a. G x con: U. Gasparini, Fisica I 14

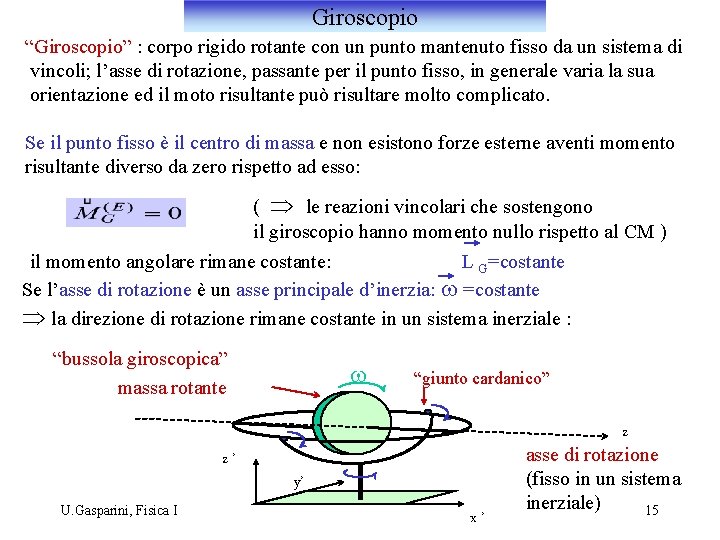
Giroscopio “Giroscopio” : corpo rigido rotante con un punto mantenuto fisso da un sistema di vincoli; l’asse di rotazione, passante per il punto fisso, in generale varia la sua orientazione ed il moto risultante può risultare molto complicato. Se il punto fisso è il centro di massa e non esistono forze esterne aventi momento risultante diverso da zero rispetto ad esso: ( Þ le reazioni vincolari che sostengono il giroscopio hanno momento nullo rispetto al CM ) il momento angolare rimane costante: L G=costante Se l’asse di rotazione è un asse principale d’inerzia: w =costante Þ la direzione di rotazione rimane costante in un sistema inerziale : “bussola giroscopica” massa rotante z’ U. Gasparini, Fisica I w “giunto cardanico” y’ x’ z asse di rotazione (fisso in un sistema inerziale) 15

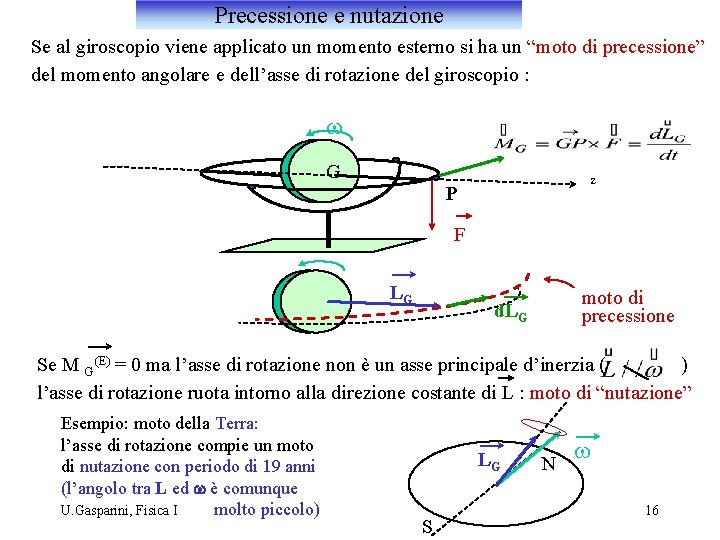
Precessione e nutazione Se al giroscopio viene applicato un momento esterno si ha un “moto di precessione” del momento angolare e dell’asse di rotazione del giroscopio : w G z P F LG moto di precessione d. LG Se M G(E) = 0 ma l’asse di rotazione non è un asse principale d’inerzia ( ) l’asse di rotazione ruota intorno alla direzione costante di L : moto di “nutazione” Esempio: moto della Terra: l’asse di rotazione compie un moto di nutazione con periodo di 19 anni (l’angolo tra L ed w è comunque U. Gasparini, Fisica I molto piccolo) LG S N w 16

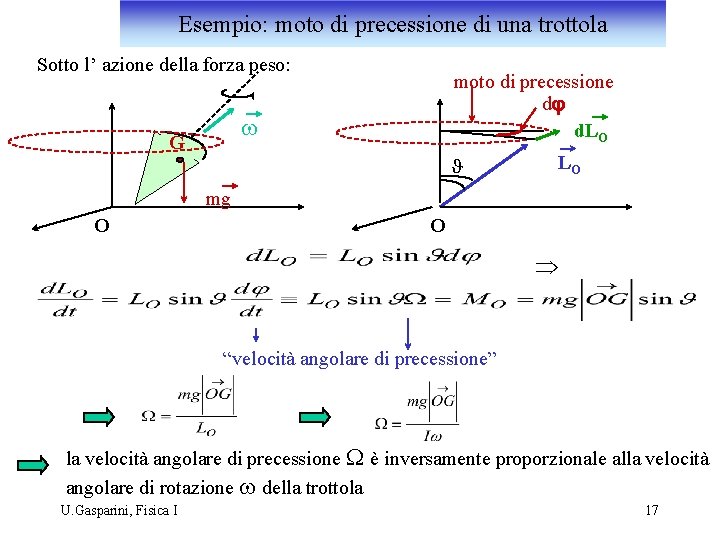
Esempio: moto di precessione di una trottola Sotto l’ azione della forza peso: moto di precessione dj d. LO w G J LO mg O O Þ “velocità angolare di precessione” la velocità angolare di precessione W è inversamente proporzionale alla velocità angolare di rotazione w della trottola U. Gasparini, Fisica I 17