Moment of a force n n The moment

Moment of a force n n The moment of a force about a point or axis provides a measure of the tendency of the force to cause a body to rotate about the point or axis Sometimes called “torque” but most often called “moment of a force” or simply the moment

Determining the moment of a force (2 -D scalar form) n n n n The magnitude of the moment MO of a force F about a point O is F d, where d is the perpendicular distance from O to the line of action of the force F SHOW The larger the force F, or the greater the distance d, the more pronounced the effect The direction of MO is specified using the “right-hand rule” – the fingers of the right hand are curled such that they follow the sense of rotation (if the force could rotate about the point O), the thumb then points along the moment axis The moment of a force will be positive if it is directed along the +z axis and negative if it is directed along the –z axis If the line of action of the force, F, passes through the point, O, d=0 – no moment produced about O – no tendency for rotation possible The dimensions of moments are “distance x force” (i. e. N-m or lb-ft) Can determine the sum of the moments of a system of forces about a point if the forces are 2 -D (coplanar) and the point lies in the same plane (can add all the moment vectors algebraically since all the moment vectors are collinear)

Cross product n n n Cross product, A x B, “A cross B” Result of cross product is a vector (vector product of vectors) C = A x B = (AB sin θ) uc – Magnitude: AB sin θ – Direction: perpendicular to the plane containing A and B and is specified by the right-hand rule (curling the fingers of the right hand from A (cross) to B, the thumb points in the direction of the uc) n Laws of operation – Commutative law is not valid: A x B ≠ B x A, A x B = -B x A – Multiplication by a scalar: a (A x B) = (a A) x B = A x (a B) = (A x B) a – Distributive law: A x (B + D) = (A x B) + (A x D)

Cartesian vector formulation n n i x i = (1)(1) sin 0° = (1)(1)(0) = 0 i x j = (1)(1) sin 90° = (1)(1)(1), direction by right-hand rule, k (SHOW) i x k = (1)(1) sin 90° = (1)(1)(1), direction by right-hand rule, -j Similarly, ixi=0 j x i = -k kxi=j ixj=k jxj=0 k x j = -i i x k = -j jxk=i kxk=0

Cross product of two general vectors n A x B = (Axi + Ayj + AZk) x (Bxi + Byj + BZk) = Ax. Bx (i x i) + Ax. By (i x j) + Ax. BZ (i x k) + Ay. Bx (j x i) + Ay. By (j x j) + Ay. Bz (j x k) + Az. Bx (k x i) + Az. By (k x j) + Az. Bz (k x k) = Ax. Bx (0) + Ax. By (k) + Ax. BZ (-j) + Ay. Bx (-k) + Ay. By (0) + Ay. Bz (i) + Az. Bx (j) + Az. By (-i) + Az. Bz (0) = (Ay. Bz – Az. By)i + (Az. Bx – Ax. BZ)j + (Ax. By – Ay. Bx)k, or = (Ay. Bz – Az. By)i - (Ax. BZ - Az. Bx)j + (Ax. By – Ay. Bx)k n Determinant form, SHOW

Moment of a force (vector form) n n n Mo = r x F, where r is the position vector from O to any point on the line of action of F Magnitude of MO: MO = r F sin θ = (r sin θ) F = d F SHOW Direction of MO follows the right-hand rule as it applies to the cross product, “r cross F” – extending r along its line of action, the fingers of right hand are curled such that they follow the sense of rotation – the thumb then points along the moment axis – giving the direction of the moment vector Result does not depend on where r intersects the line of action of F, r. OB x F = (r. OA + r. AB) x F = r. OA x F SHOW Principle of transmissibility: F is a sliding vector – it can act at any point along its line of action and still create the same moment about point O A moment is denoted with a circular arrow around the vector (a curl) SHOW

In Cartesian vector form n MO = r x F = + - + i j k rx ry rz Fx Fy Fz MO = (ry. Fz – rz. Fy) i - (rx. Fz – rz. Fx) j + (rx. Fy – ry. Fx) k

Principle of Moments (Varignon’s Theorem) n The moment of a force about a point is equal to the sum of the moments of the force’s components about the point (SHOW) MO = (r x F 1) + (r x F 2) = r x (F 1 + F 2) n EXAMPLES (pg 138 - 144)

Moment of a force about a line (scalar analysis) n n Two-step process Direct process - if the line of action of the force F is perpendicular to any specified axis aa, the magnitude of the moment of F about the axis can be determined from Ma = F da, where da is the perpendicular or shortest distance from the force line of action to the axis

Moment of a force about a line (vector analysis) n n n Component of MO parallel to aa', Ma = ua ∙ MO, where ua is a unit vector along aa’ Substituting MO = r x F in above, Ma = ua ∙ (r x F) Can write Ma = ua ∙ MO = ua ∙ (r x F) as a scalar triple product M a = u a ∙ MO = n n n + - + uax uay uaz rx ry rz Fx Fy Fz The scalar Ma determines both the magnitude and sense of direction of Ma. If Ma is positive, Ma will have the same sense as ua, and if Ma is negative, then Ma will act opposite to ua. Expressing Ma as a Cartesian vector, Ma = Ma ua = [ua ∙ (r x F)] ua EXAMPLES (pgs 152 - 153)

A couple n n n A couple consists of two forces that have equal magnitudes, same directions, but opposite senses Parallel, distinct lines of action SHOW The resultant force is zero, the only effect is to produce a rotation

Moment of a couple (scalar formulation) n The moment of the couple M is defined as having a magnitude of M = F d F is the magnitude of one of the forces d is the perpendicular distance or moment arm between the forces n The direction and sense of the couple moment are determined by the right-hand rule (where thumb indicates the direction when the fingers are curled with the sense of rotation caused by the two forces – M acts perpendicular to the plane containing the two forces)

Moment of a couple (vector formulation) n A couple moment: is equal to the sum of the moments of both couple forces determined about any arbitrary point O in space SHOW M = r. A x (-F) + r. B x F M = - r. A x F + r. B x F M = ( r. B + - r. A) x F = ( r. B – r. A) x F = r x F n n n A couple moment is a free vector – it can act at any point, since M only depends on r, not r. A or r. B r is directed from any point on the line of action of one of the forces to any point on the line of action of the other force EXAMPLES (pg 161 - 165)

Equivalent systems n n n A system of forces and couple moments can be represented by a single force acting at a given point and a single couple moment To do so it is necessary that the force and couple moment system produce the same "external" effects of translation and rotation of the body as their resultants Two systems of forces and couple moments (system 1 and system 2) are equivalent if: the sums of the forces are equal, (∑ F)1 = (∑ F)2 and the sums of the moments about a point P are equal, (∑ Mp)1 = (∑ Mp)2 n EXAMPLES (pg 174 – 176)

Special cases that occur n n n Concurrent forces represented by a force Coplanar forces represented by a force Parallel forces represented by a force

Representing a system by a wrench n n The wrench consists of the force FR acting at a point P and the parallel component Mp. The point P must be chosen so that the moment of FR about P equals the normal component Mn, r. OP x FR = Mn (SHOW) EXAMPLES (pg 186 – 189)

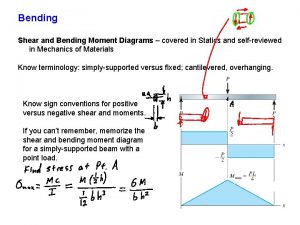
Simple Distributed Loading n n n Plate supports the loading over its surface Loading function, p = p(x) (Pa), is only a function of x since the pressure is uniform along the y axis Multiply p = p(x) by the width a (m) of the plate, w = p(x) (N/m 2) a (m) = w(x) (N/m) d. F is acting on an infinitesimally thin element of width dx, d. F = w(x) dx (= d. A, in terms of the “area” A under the curve) Can replace this coplanar parallel force system with a single equivalent resultant force The magnitude of the resultant force is equal to the total area A under the loading diagram w=w(x)

Location of the Resultant Force for a Simple Distributed Loading n Location of to the line of action of FR can be determined by equating the moments of the force resultant and the force distribution about point O n The resultant force has a line of action which passes through the centroid C (the geometric center) of the area defined by the distributed-loading diagram w(x) Often the distributed-loading diagram is in the shape of a rectangle, triangle, or some other simple geometric form EXAMPLES (pg 196 - 200) n n