Modlisation des pics de crue comme phnomnes critiques

















- Slides: 32

Modélisation des pics de crue comme phénomènes critiques: de la théorie des files d'attente à la physique statistique. Emmanuel Mouche, Marie Alice Harel (LSCE) Michel Bauer (IPh. T) 17/05/2017

Outline • Hydrologic context • Connectivity issue • 1 D & 2 D Models • Queueing theory • Statistical physics approaches

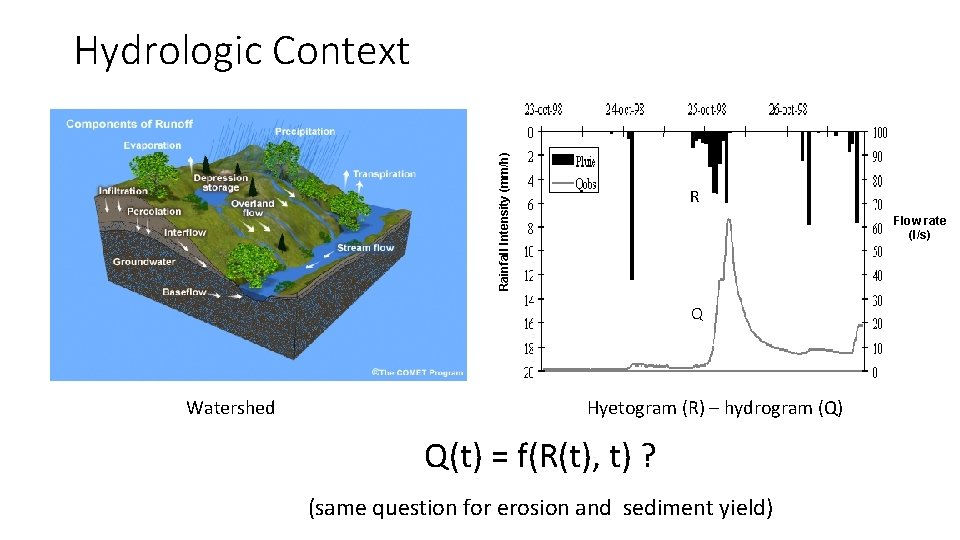
Rainfall Intensity (mm/h) Hydrologic Context R Flow rate (l/s) Q Watershed Hyetogram (R) – hydrogram (Q) Q(t) = f(R(t), t) ? (same question for erosion and sediment yield)

Infiltration and Runoff (ruissellement) Infiltration model Diffuse runoff and runoff in rills R > I 1 : Infiltration and runoff R < I 2 : Infiltration ! Ponding time

Runoff runon (ruissellement réinfiltration) t 1 Runoff Diffuse runoff and runoff in rills t 2 Runoff runon t 3 Coalescence

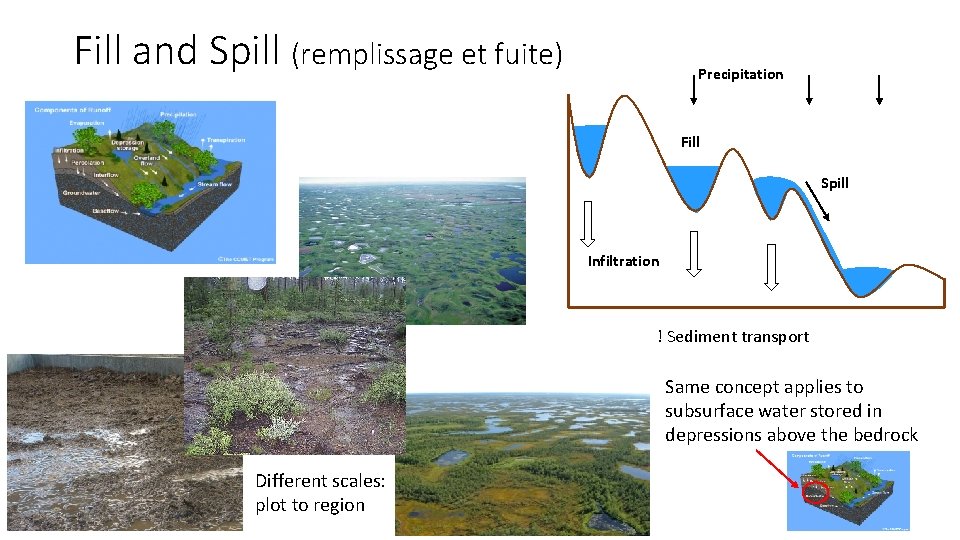
Fill and Spill (remplissage et fuite) Precipitation Fill Spill Infiltration ! Sediment transport Same concept applies to subsurface water stored in depressions above the bedrock Different scales: plot to region

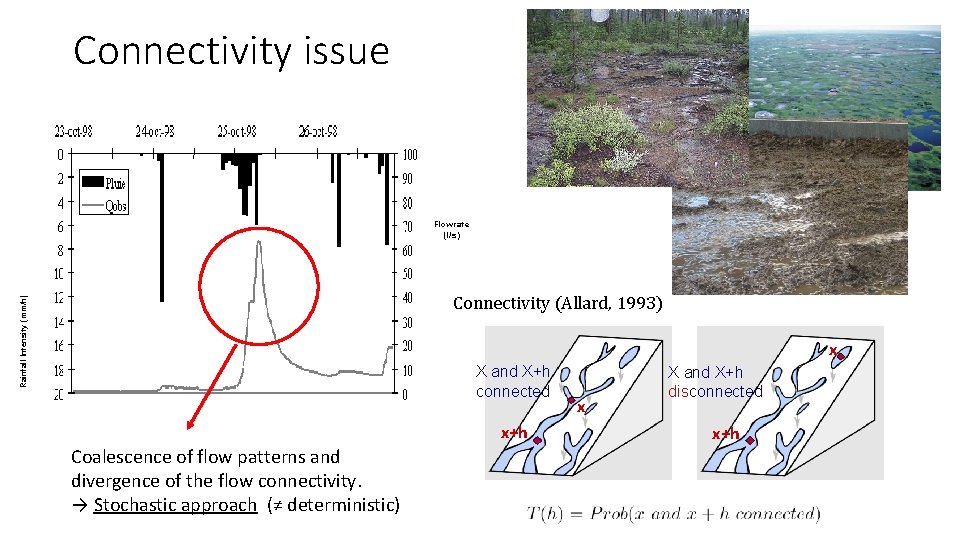
Connectivity issue Flow rate (l/s) Rainfall Intensity (mm/h) Connectivity (Allard, 1993) x X and X+h connected x+h Coalescence of flow patterns and divergence of the flow connectivity. → Stochastic approach (≠ deterministic) x X and X+h disconnected x+h

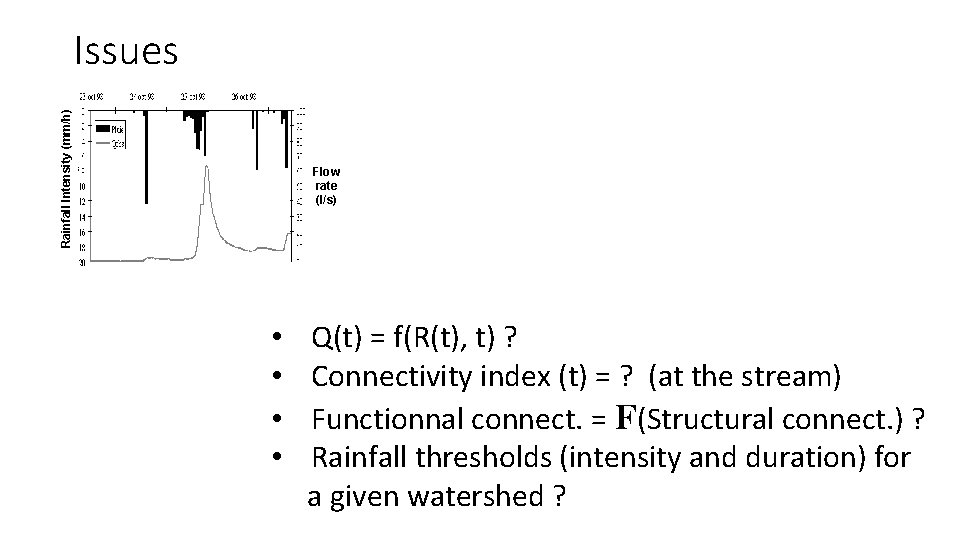
Rainfall Intensity (mm/h) Issues Flow rate (l/s) • • Q(t) = f(R(t), t) ? Connectivity index (t) = ? (at the stream) Functionnal connect. = F(Structural connect. ) ? Rainfall thresholds (intensity and duration) for a given watershed ?

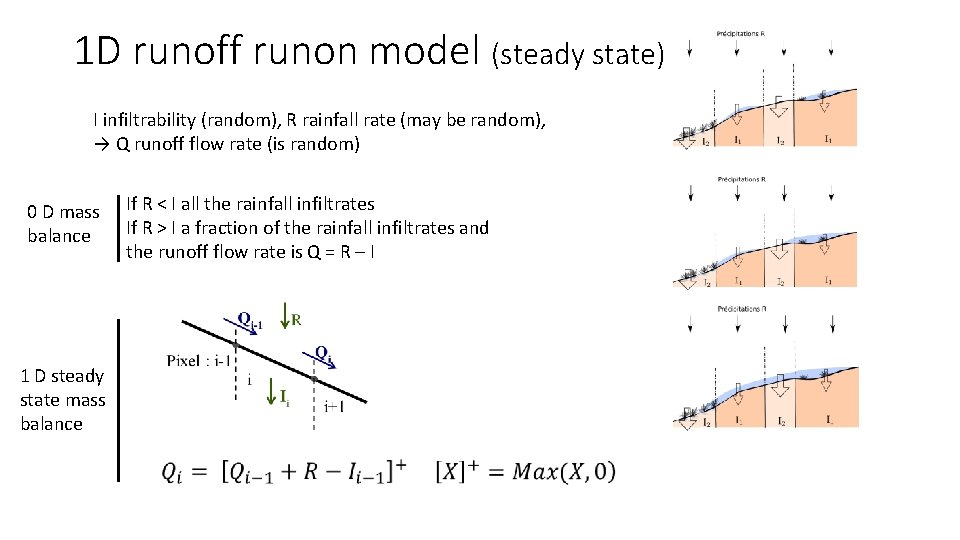
1 D runoff runon model (steady state) I infiltrability (random), R rainfall rate (may be random), → Q runoff flow rate (is random) 0 D mass balance If R < I all the rainfall infiltrates If R > I a fraction of the rainfall infiltrates and the runoff flow rate is Q = R – I 1 D steady state mass balance

2 D runoff runon model (steady state) I infiltrability, R rainfall rate, Q runoff flow rate 2 D steady state mass balance Where ε is a mixing (or dispersion) factor. May be random (εij) to simulate channels or rills.

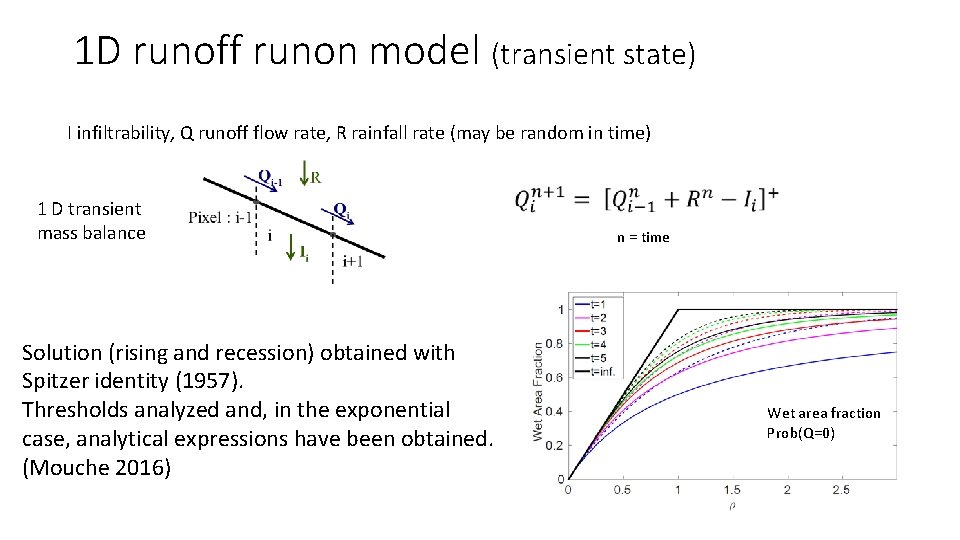
1 D runoff runon model (transient) I infiltrability, Q runoff flow rate, R rainfall rate (may be random in time) 1 D transient mass balance If Courant number = 1 and transport is linearized and ponding time is neglected n = time

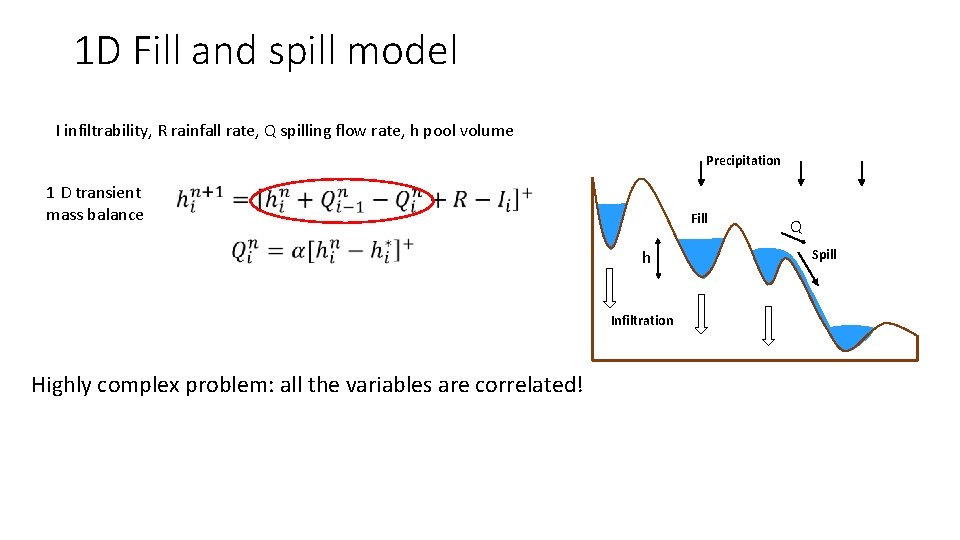
1 D Fill and spill model I infiltrability, R rainfall rate, Q spilling flow rate, h pool volume Precipitation 1 D transient mass balance Fill If I = 0 no steady state h Infiltration Q h* Spill

1 D runoff runon model (steady) I infiltrability, Q runoff flow rate, R rainfall rate Transport equation with positivity constraint (Max plus algebra, cellular automaton). - Random walk with a special boundary condition at x=0: X(t+dt) = [X(t) + f(t)]+ - Queueing theory - Ruin problems in mechanics, … (see Feller, « An intro. to probability theory » )

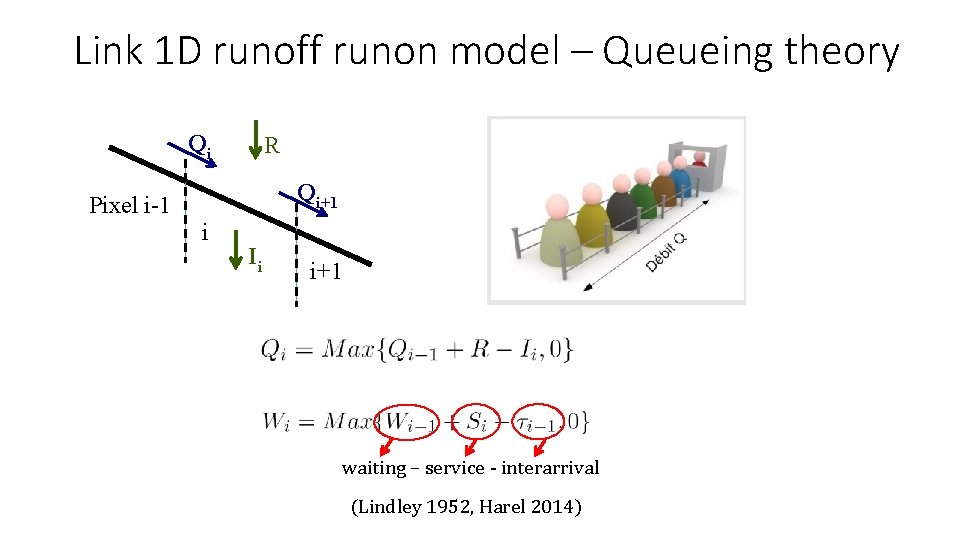
Link 1 D runoff runon model – Queueing theory Qi R Qi+1 Pixel i-1 i Ii i+1 waiting – service - interarrival (Lindley 1952, Harel 2014)

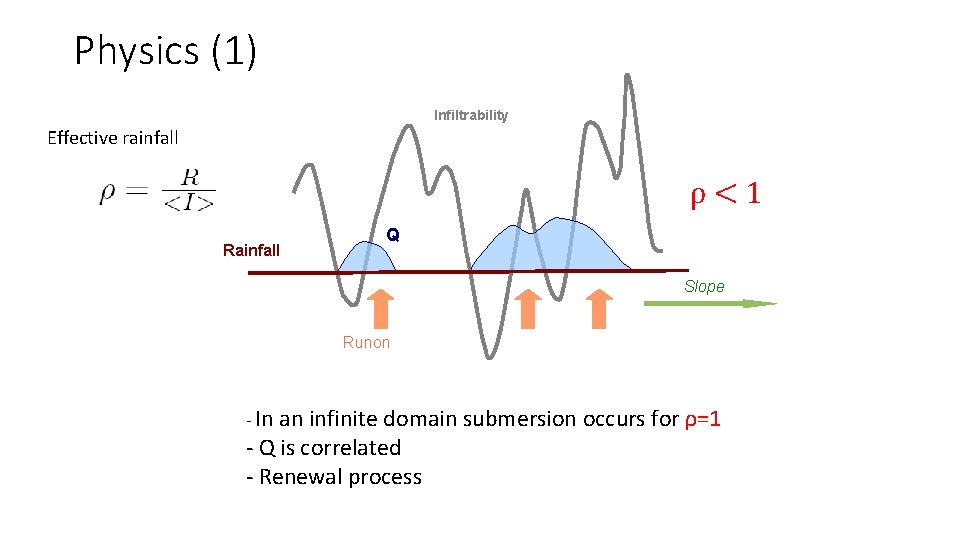
Physics (1) Infiltrability Effective rainfall ρ<1 Rainfall Q Slope Runon - In an infinite domain submersion occurs for ρ=1 - Q is correlated - Renewal process

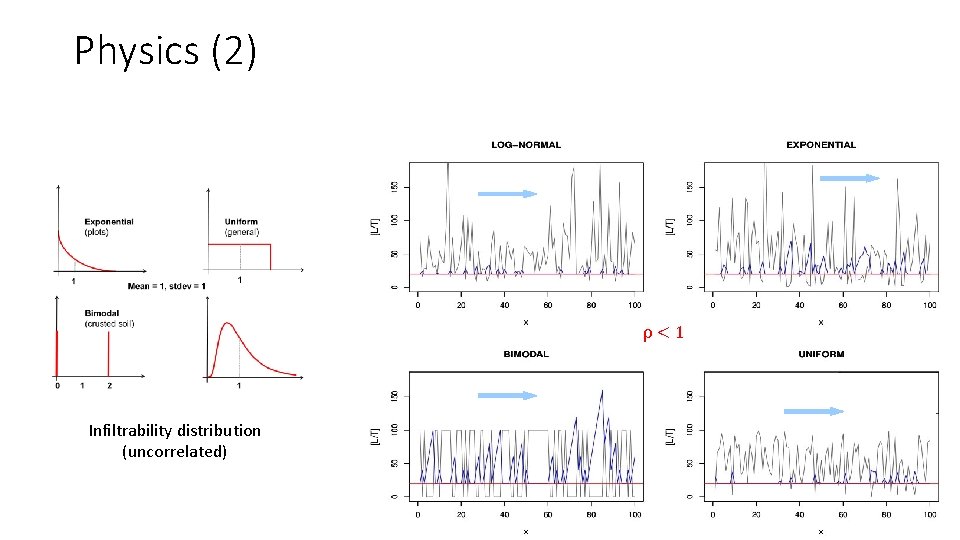
Physics (2) ρ<1 Infiltrability distribution (uncorrelated)

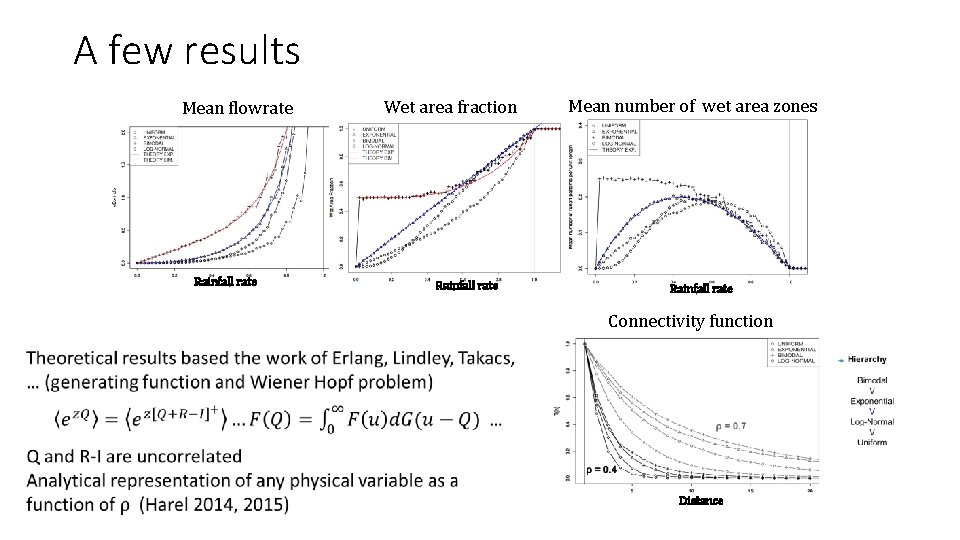
A few results Mean flowrate Rainfall rate Wet area fraction Rainfall rate Mean number of wet area zones Rainfall rate Connectivity function Distance

The bimodal queue The only known queue with Pd. F discontinuities No analytical representation of the physical variables as functions of ρ (Mouche 2016) The discrete generating function of the problem leads to a characteristic polynomial which exponents are discontinuous functions of ρ. α and β are the prob. of the two modes (α + β = 1)

1 D runoff runon model (transient state) I infiltrability, Q runoff flow rate, R rainfall rate (may be random in time) 1 D transient mass balance Solution (rising and recession) obtained with Spitzer identity (1957). Thresholds analyzed and, in the exponential case, analytical expressions have been obtained. (Mouche 2016) n = time Wet area fraction Prob(Q=0)

2 D runoff runon model (steady) (Work done in collab. with Michel Bauer of SPh. T) I infiltrability, R rainfall rate, Q runoff flow rate 2 D steady state mass balance (Harel 2016)

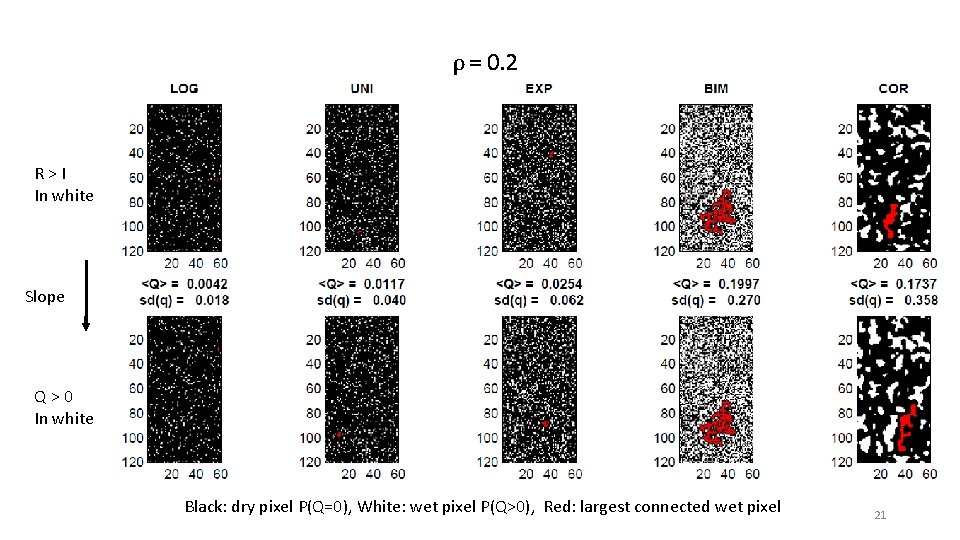
ρ = 0. 2 R > I In white Slope Q > 0 In white Black: dry pixel P(Q=0), White: wet pixel P(Q>0), Red: largest connected wet pixel 21

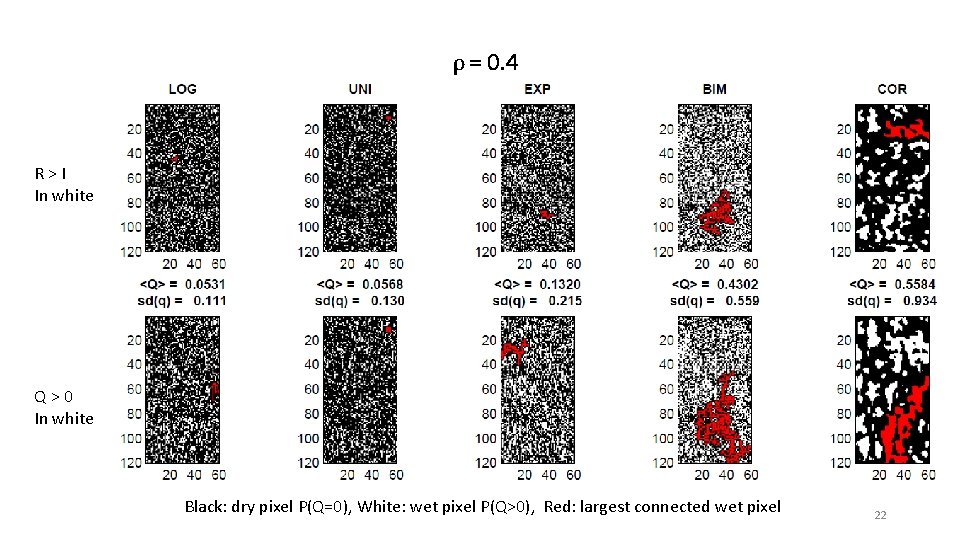
ρ = 0. 4 R > I In white Q > 0 In white Black: dry pixel P(Q=0), White: wet pixel P(Q>0), Red: largest connected wet pixel 22

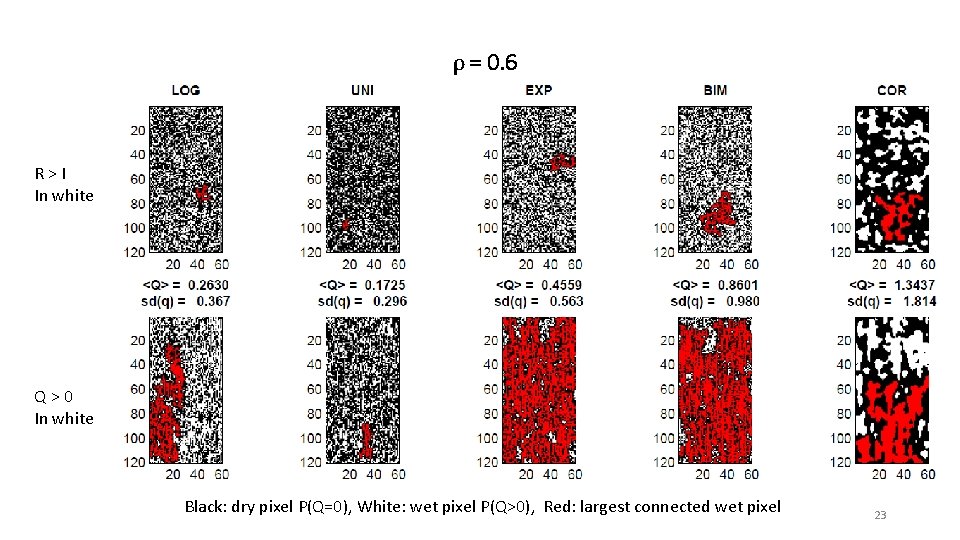
ρ = 0. 6 R > I In white Q > 0 In white Black: dry pixel P(Q=0), White: wet pixel P(Q>0), Red: largest connected wet pixel 23

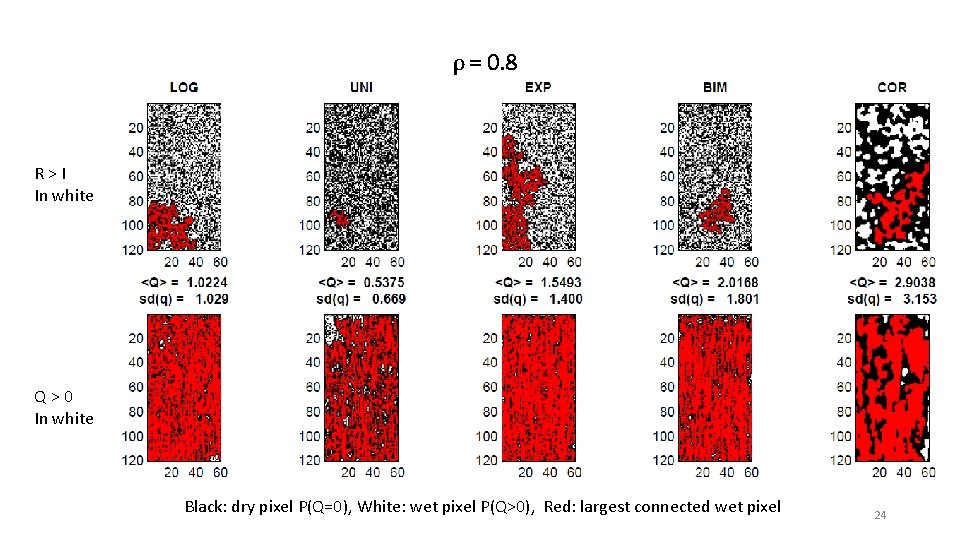
ρ = 0. 8 R > I In white Q > 0 In white Black: dry pixel P(Q=0), White: wet pixel P(Q>0), Red: largest connected wet pixel 24

2 D runoff runon model (steady) I infiltrability, R rainfall rate, Q runoff flow rate 2 D steady state mass balance If i is considered as time axis we have the transient diffusion equation with positivity constraint At steady state Advection Diffusion

It does not describe a renewal process. The equation must be solved at the whole scale of a pattern. Numerically the transient state must be solved to obtain the steady state. Submersion occurs for ρ = 1 (physics) ρ = 0. 1 ρ = 0. 2 ρ = 0. 5 ρ = 0. 7 ρ = 0. 9 • Probably anomalous diffusion (extremely long relaxation times for high rho values). • The wet area fraction does not depend on the type of equation (diff. or adv. ) and on the dimension (1 D or 2 D) !. • M. Bauer propose to solve « iteratively » the problem starting from the divergence ρ = 1

Following the recent work of Boxma (2016) on we solve We show that the wet area fraction (Prob(Q=0))is independent of ε. We obtain a relationship between the mean flowrate Q and its covariance Connectivity ?

Statistical physics approaches •

Renormalization (1) • I 1 , R I 2 , R I 3 , R I 4, R I’(I 1 , I 2 , …, 4 R) « à la Kadanoff » The Pd. F P(I’=n. R) is known !

Renormalization (2): the sandpile problem (Bak 1987)

Correlated percolation

1 D Fill and spill model I infiltrability, R rainfall rate, Q spilling flow rate, h pool volume Precipitation 1 D transient mass balance Fill h Infiltration Highly complex problem: all the variables are correlated! Q Spill
 Crue
Crue Je nais et meurs dans l'eau. qui suis-je
Je nais et meurs dans l'eau. qui suis-je Oh quel beau jour
Oh quel beau jour O quel beau jour ou devant ta face
O quel beau jour ou devant ta face Des des des
Des des des Site master file
Site master file Mig welding pictures
Mig welding pictures Divers who act foolishly at depth
Divers who act foolishly at depth Pics of primary sector
Pics of primary sector Std crabs pics
Std crabs pics Pic pharmaceutical inspection convention
Pic pharmaceutical inspection convention Individual pics
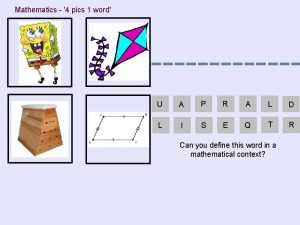
Individual pics 4 pics 1 word mathematics version
4 pics 1 word mathematics version Busty mature tube
Busty mature tube Pics hermetic bags
Pics hermetic bags Aunt jennifer's tigers art integrated project
Aunt jennifer's tigers art integrated project How many parts of computer
How many parts of computer Pic architecture
Pic architecture Robyn fenty real name
Robyn fenty real name Malnutrition pics
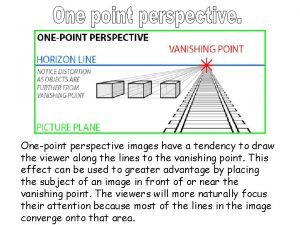
Malnutrition pics One point perspective pics
One point perspective pics 100 pics say what you see
100 pics say what you see Humanist beliefs on euthanasia
Humanist beliefs on euthanasia Good morning happy november
Good morning happy november Http://solarsystem.nasa.gov/planets/
Http://solarsystem.nasa.gov/planets/ Flagellated fungi
Flagellated fungi Pics princeton
Pics princeton Transitional epithelium layers
Transitional epithelium layers Dukes criteria
Dukes criteria Aristotle pics
Aristotle pics Learning without burden was published in
Learning without burden was published in Yandex.com images
Yandex.com images Atiqur rahman ahad
Atiqur rahman ahad