Matire Mathmatique Statistique Solutions Srie dexercices N 03

Matière: Mathématique / Statistique Solutions: Série d’exercices N° 03 Réalisé par: Dr: Maifi Lyes

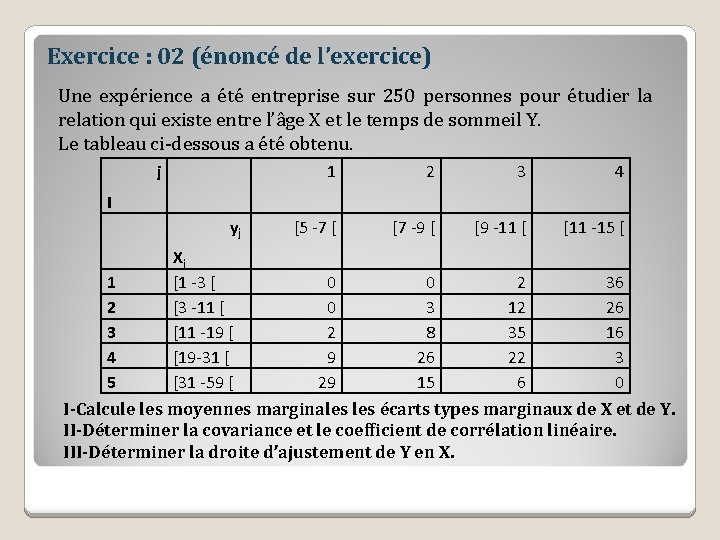
Exercice : 02 (énoncé de l’exercice) Une expérience a été entreprise sur 250 personnes pour étudier la relation qui existe entre l’âge X et le temps de sommeil Y. Le tableau ci-dessous a été obtenu. j 1 2 3 4 [5 -7 [ [7 -9 [ [9 -11 [ [11 -15 [ 0 0 2 9 29 0 3 8 26 15 2 12 35 22 6 36 26 16 3 0 I yj 1 2 3 4 5 Xi [1 -3 [ [3 -11 [ [11 -19 [ [19 -31 [ [31 -59 [ I-Calcule les moyennes marginales écarts types marginaux de X et de Y. II-Déterminer la covariance et le coefficient de corrélation linéaire. III-Déterminer la droite d’ajustement de Y en X.

I-1 -Calculer les moyennes marginales - Suivant x: Avec n. T c’est l’effectifs total égale à 250 à partir de l’exercice. Initialement il faut calculer ni (i=1 : 5). On a : ni c’est la somme des effectifs qui ont le même caractère xi Donc : n 1=n 11+n 12+n 13+n 14=0+0+2+36=38 n 2=n 21+n 22+n 23+n 24=0+3+12+26=41 n 3=n 31+n 32+n 33+n 34=2+8+35+16=61 n 4=n 41+n 42+n 43+n 44=9+26+22+3=60 n 5=n 51+n 52+n 53+n 54=29+15+6+0=50 Remarque: Et xi c’est le centre des classes i de forme [ei-1 -ei[ ,

e 1= (1+3)/2=2 e 2= (3+11)/2=7 e 3= (11+19)/2=15 e 4= (19+31)/2=25 e 5= (31+59)/2=45 Résultat:

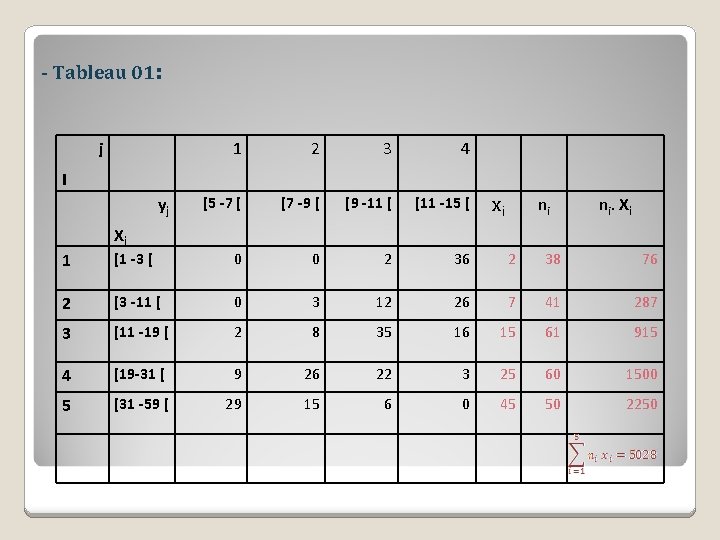
- Tableau 01: j 1 2 3 4 [5 -7 [ [7 -9 [ [9 -11 [ [11 -15 [ I yj Xi ni xi ni. X i 1 [1 -3 [ 0 0 2 36 2 38 76 2 [3 -11 [ 0 3 12 26 7 41 287 3 [11 -19 [ 2 8 35 16 15 61 915 4 [19 -31 [ 9 26 22 3 25 60 1500 5 [31 -59 [ 29 15 6 0 45 50 2250

- Suivant y: Avec n. T c’est l’effectifs total égale à 250 à partir de l’exercice. Initialement il faut calculer nj (j=1 : 4). On a : ni c’est la somme des effectifs qui ont le même caractère yj Donc : n 1=n 11+n 21+n 31+n 41+n 51=0+0+2+9+29=40 n 2=n 12+n 22+n 32+n 42+n 52=0+3+8+26+15=52 n 3=n 13+n 23+n 33+n 43+n 53=2+12+35+22+6=77 n 4=n 14+n 24+n 34+n 44+n 54=36+26+16+3+0=81 Remarque: Et yj c’est le centre des classes i de forme [ej-1–ej[ ,

e 1= (5+7)/2=6 e 2= (7+9)/2=8 e 3= (9+11)/2=10 e 4= (11+15)/2=13 Résultat:

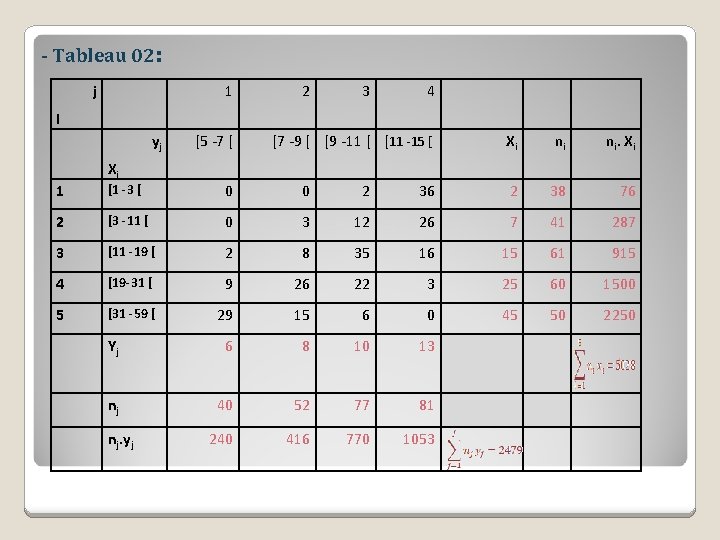
- Tableau 02: j 1 2 3 4 I yj [5 -7 [ [7 -9 [ [9 -11 [ [11 -15 [ Xi ni ni. Xi Xi 1 [1 -3 [ 0 0 2 36 2 38 76 2 [3 -11 [ 0 3 12 26 7 41 287 3 [11 -19 [ 2 8 35 16 15 61 915 4 [19 -31 [ 9 26 22 3 25 60 1500 5 [31 -59 [ 29 15 6 0 45 50 2250 Yj 6 8 10 13 nj 40 52 77 81 240 416 770 1053 nj. yj

I-2 -Calculer les écarts types marginaux de X et de Y - Suivant x: On a: L’écart type suivant (x) Donc pour calculer L’écart type suivant x il faut d’abord calculer la variance (var(x)) Résultat:

- Tableau 03: j 1 2 3 4 I yj [5 -7 [ [7 -9 [ [9 -11 [ [11 -15 [ Xi ni ni. Xi n i xi 2 Xi 1 [1 -3 [ 0 0 2 36 2 38 76 152 2 [3 -11 [ 0 3 12 26 7 41 287 2009 3 [11 -19 [ 2 8 35 16 15 61 915 13725 4 [19 -31 [ 9 26 22 3 25 60 1500 37500 5 [31 -59 [ 15 6 0 45 50 2250 101250 Yj 29 6 8 10 13 nj 40 52 77 81 240 416 770 1053 nj. yj

- Suivant y: On a: L’écart type suivant (y) Donc pour calculer L’écart type suivant y il faut d’abord calculer la variance (var(y)) Résultat:

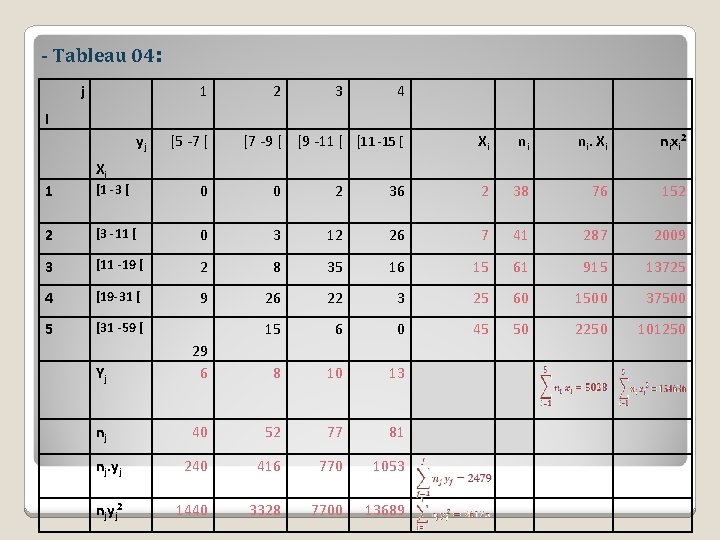
- Tableau 04: j 1 2 3 4 I yj [5 -7 [ [7 -9 [ [9 -11 [ [11 -15 [ Xi ni ni. Xi n i xi 2 Xi 1 [1 -3 [ 0 0 2 36 2 38 76 152 2 [3 -11 [ 0 3 12 26 7 41 287 2009 3 [11 -19 [ 2 8 35 16 15 61 915 13725 4 [19 -31 [ 9 26 22 3 25 60 1500 37500 5 [31 -59 [ 15 6 0 45 50 2250 101250 Yj 29 6 8 10 13 nj 40 52 77 81 nj. yj 240 416 770 1053 nj yj 2 1440 3328 7700 13689

II-1 -Calculer la covariance cov(x, y)

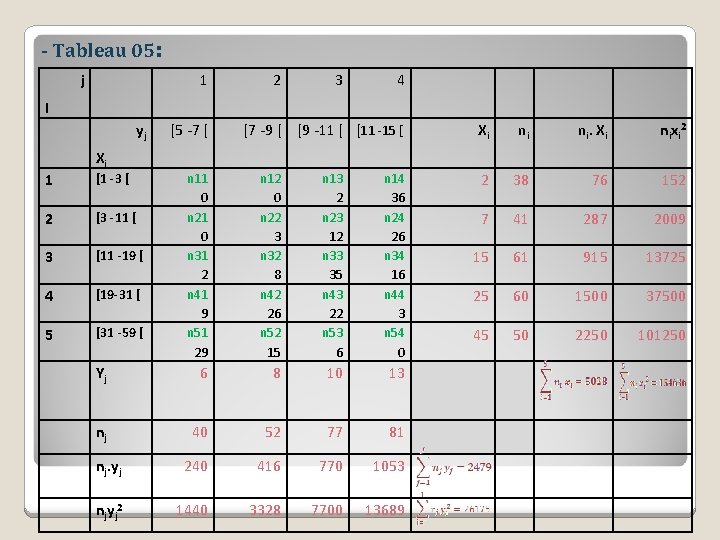
- Tableau 05: j 1 2 3 4 I yj Xi 1 [1 -3 [ 2 [3 -11 [ 3 [11 -19 [ 4 [19 -31 [ 5 [31 -59 [ [5 -7 [ [7 -9 [ [9 -11 [ [11 -15 [ n 11 0 n 21 0 n 31 2 n 41 9 n 51 29 n 12 0 n 22 3 n 32 8 n 42 26 n 52 15 n 13 2 n 23 12 n 33 35 n 43 22 n 53 6 n 14 36 n 24 26 n 34 16 n 44 3 n 54 0 Yj 6 8 10 13 nj 40 52 77 81 nj. yj 240 416 770 1053 nj yj 2 1440 3328 7700 13689 Xi ni ni. Xi n i xi 2 2 38 76 152 7 41 287 2009 15 61 915 13725 25 60 1500 37500 45 50 2250 101250

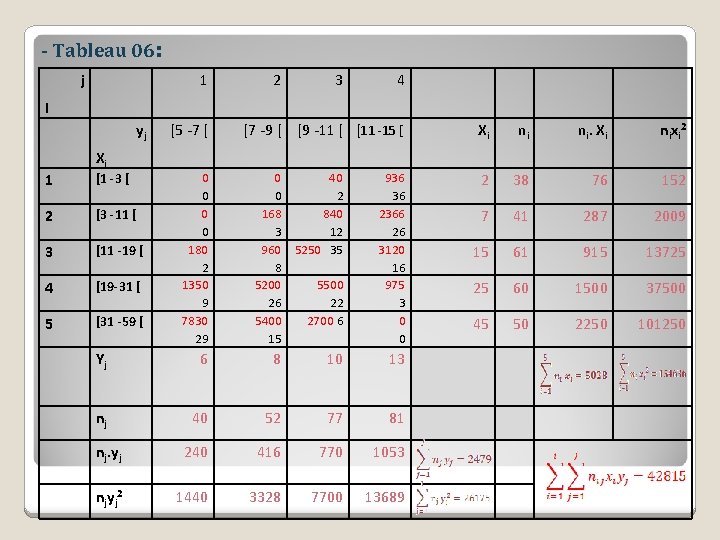
- Tableau 06: j 1 2 3 4 I yj Xi [5 -7 [ [7 -9 [ [9 -11 [ [11 -15 [ 0 0 180 2 1350 9 7830 29 0 0 168 3 960 8 5200 26 5400 15 40 2 840 12 5250 35 Yj 6 8 10 13 nj 40 52 77 81 nj. yj 240 416 770 1053 nj yj 2 1440 3328 7700 13689 1 [1 -3 [ 2 [3 -11 [ 3 [11 -19 [ 4 [19 -31 [ 5 [31 -59 [ 5500 22 2700 6 936 36 2366 26 3120 16 975 3 0 0 Xi ni ni. Xi n i xi 2 2 38 76 152 7 41 287 2009 15 61 915 13725 25 60 1500 37500 45 50 2250 101250

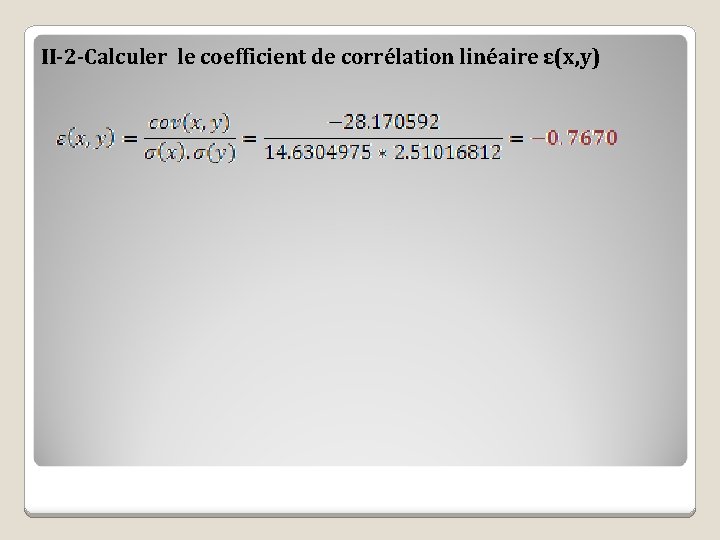
II-2 -Calculer le coefficient de corrélation linéaire ε(x, y)

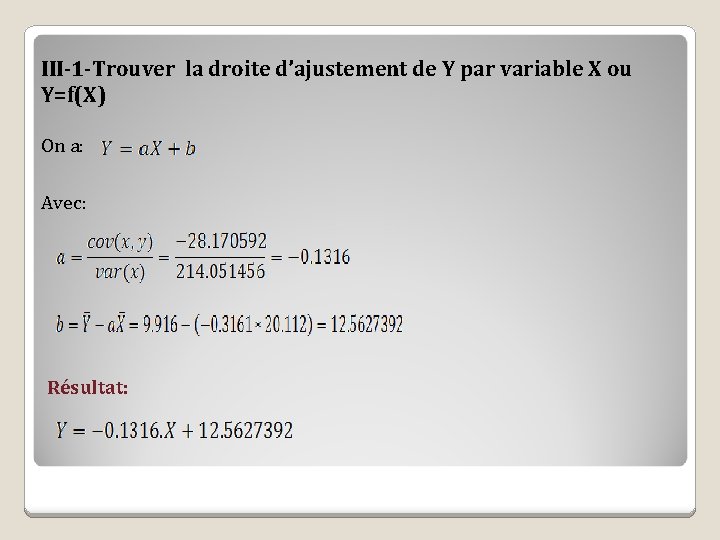
III-1 -Trouver la droite d’ajustement de Y par variable X ou Y=f(X) On a: Avec: Résultat: