Matemticas II Departamento de Economa Aplicada Universidad de

Matemáticas II Departamento de Economía Aplicada Universidad de La Laguna Proyecto: OPEN COURSE WARE 2012 Profesores que participan en el Proyecto: Marianela Carrillo Fernández Domingo Israel Cruz Báez Concepción González Concepción Juan Carlos Moreno Piquero Celina Pestano Gabino (Coordinadora) José Enrique Rodríguez Hernández

Optimizar Buscar la “mejor solución” a un problema dado ¿ Por qué ? Normalmente los recursos o medios disponibles son limitados y queremos conseguir una asignación “óptima”

Tema: Optimización clásica Bajo “ciertas condiciones de diferenciabilidad” y bajo “ciertas condiciones de regularidad”

Tema: Optimización clásica Optimización libre Optimizar f(x 1, x 2, …xn) Optimización condicionada Optimizar f(x 1, x 2, …xn) sujeto a g 1(x 1, x 2, …xn)=0 g 2(x 1, x 2, …xn)=0 …

Tema: Optimización clásica z=f(x 1, x 2, …xn) n=1 y=f(x) n=1 y=f(x) Curvas en el plano y Máximo relativo Mínimo relativo Punto inflexión x

Tema: Optimización clásica z=f(x 1, x 2, …xn) n=1 y=f( x) Procedimiento: > 0 Mínimo relat. y’=0 x=a puntos críticos y’’ (a) < 0 Máximo relat. = 0 Duda

Tema: Optimización clásica z=f(x 1, x 2, …xn) n=1 y=f( x) Desarrollo de Taylor: x=a puntos críticos y’ (a)=f’(a)=0 Mínimo relativo Máximo relativo

Tema: Optimización clásica z=f(x 1, x 2, …xn) Ejemplo: n=1 y=f( x) y= 0. 8 x 5 - 11 x 4 + 52 x 3 - 90 x 2 + 50 y´= 4 x 4 - 44 x 3 + 156 x 2 -180 x y’’ (0) < 0 Máximo rel. y’=0 x=0 , x=3, x=5 puntos críticos y’’ (5) > 0 Mínimo rel. y’’ (3) = 0 Duda y’’’ (3) ≠ 0 Punto inflexión

Tema: Optimización clásica n=1 y=f( x) z=f(x 1, x 2, …xn) Ejemplo: y’=0 C(X)= 3/4 x + 1 2 x 5 y´= 3/4 >0 creciente C x= 2 Mínimo rel. x= 5 Máximo rel. 2 5 x

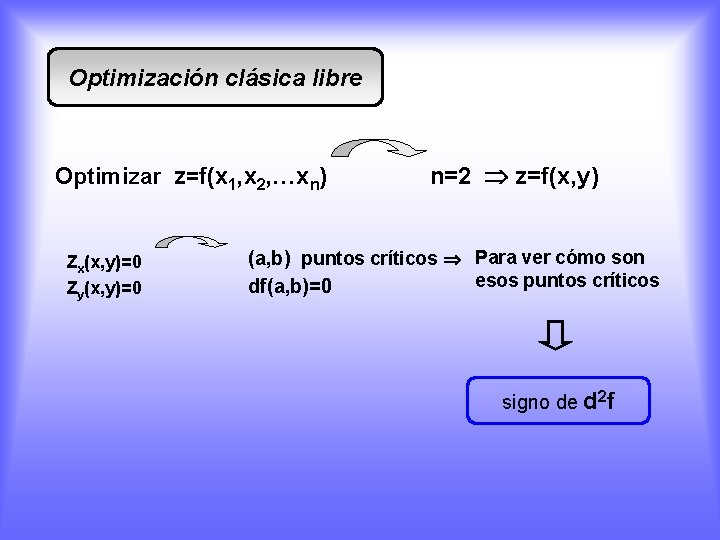
Optimización clásica libre Optimizar z=f(x 1, x 2, …xn) Zx(x, y)=0 Zy(x, y)=0 n=2 z=f(x, y) (a, b) puntos críticos Para ver cómo son esos puntos críticos df(a, b)=0 signo de d 2 f

Optimización clásica libre Optimizar z=f(x 1, x 2, …xn) n=2 z=f(x, y) signo de d 2 f Se define diferencial segunda de z: d 2 z = d(dz) = zxx(x, y)(dx)2 + 2 zxydxdy + zyy(dy)2

Optimización clásica libre signo de d 2 f Clasificación de los puntos críticos: H 1>0 H 2>0 Definida positiva (Mínimo relativo) H 1<0 H 2>0 Definida negativa (Máximo relativo) H 1<0 H 2<0; H 1>0 H 2<0 No Definida (Punto de silla)

Optimización clásica libre Ejemplo: Z(x, y)= x 2 -y 2 Zx= 2 x=0 Zy= -2 y=0 H 1= 2 >0 ; H 2=-4 <0 (0, 0) punto crítico Zxx= 2 Zxy= 0 Zyy= -2 No Def. Punto de silla

Optimización clásica libre Ejemplo: Z(x, y)= -x 2 -y 2 Zx= -2 x=0 Zy= -2 y=0 H 1= -2 <0 ; H 2= 4 >0 (0, 0) punto crítico Zxx= -2 Zxy= 0 Zyy= -2 Def. negativa Máximo relativo

Optimización clásica libre Ejemplo: Z(x, y)= (x –y)2 Zx= 2(x-y)=0 Zy= -2(x-y)=0 H 1= 2 >0 ; H 2= 0 (a, a) punto crítico Zxx(a, a) = 2 Zxy(a, a) = -2 Zyy(a, a) = 2 Semidefinida positiva f(a, a)=0 y como f (x, y) 0 los puntos (a, a) son Mínimos relativos

Optimización clásica libre Ejemplo: Z(x, y)= xy Zx= y=0 Zy= x=0 H 1= 0 ; H 2= -1 (0, 0) punto crítico Zxx(0, 0) = 0 Zxy(0, 0) = 1 Zyy(0, 0) = 0 No Def. Punto de silla

Optimización clásica libre Ejemplo: B(x, y)= -2 x 2 -2 y 2 +36 x +42 y -2 xy -75 Bx=-4 x-2 y+36=0 By=-4 y-2 x+42=0 (5, 8) punto crítico H 1=-4 <0 ; H 2=16 -4=12 >0 Bxx=-4 Bxy=-2 Byy=-4 Máximo relativo Al ser definida negativa para todo valor de x e y Máximo absoluto único

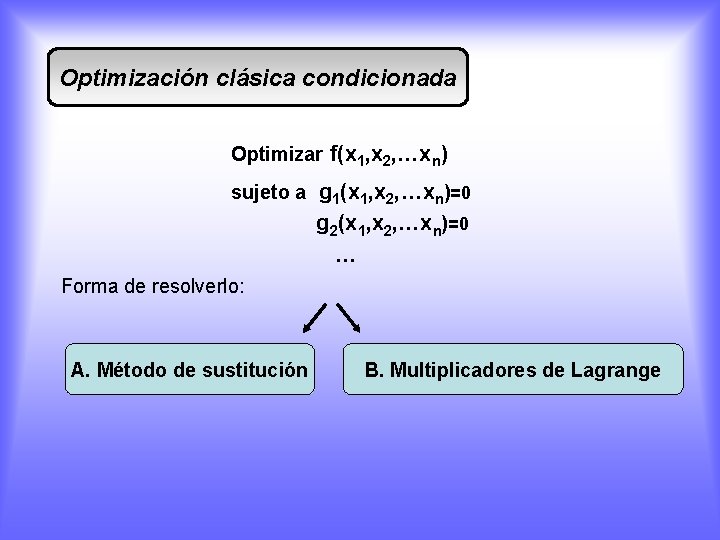
Optimización clásica condicionada Optimizar f(x 1, x 2, …xn) sujeto a g 1(x 1, x 2, …xn)=0 g 2(x 1, x 2, …xn)=0 … Forma de resolverlo: A. Método de sustitución B. Multiplicadores de Lagrange

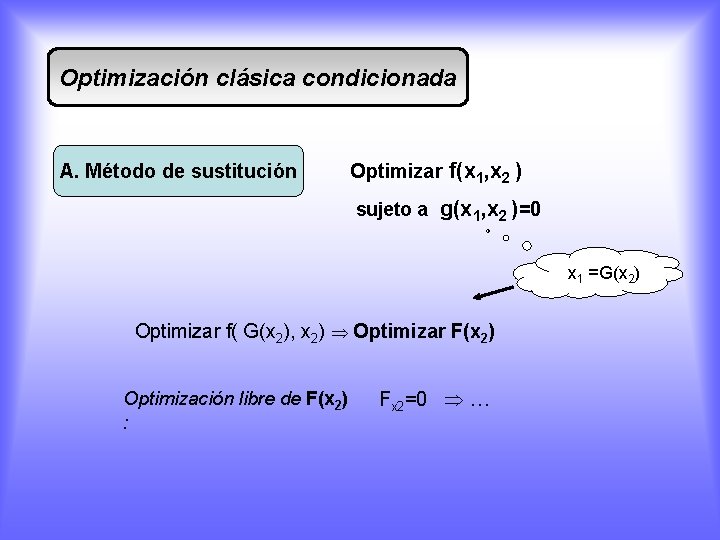
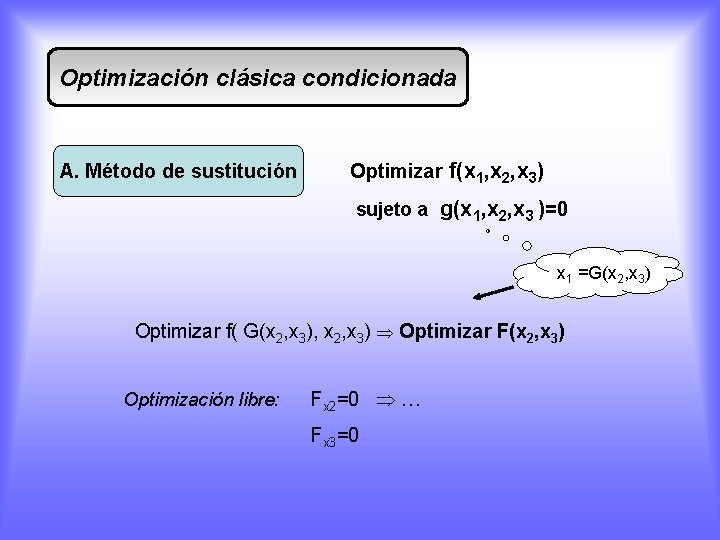
Optimización clásica condicionada A. Método de sustitución Optimizar f(x 1, x 2 ) sujeto a g(x 1, x 2 )=0 x 1 =G(x 2) Optimizar f( G(x 2), x 2) Optimizar F(x 2) Optimización libre de F(x 2) : Fx 2=0 …

Optimización clásica condicionada A. Método de sustitución Optimizar f(x 1, x 2, x 3) sujeto a g(x 1, x 2, x 3 )=0 x 1 =G(x 2, x 3) Optimizar f( G(x 2, x 3), x 2, x 3) Optimizar F(x 2, x 3) Optimización libre: Fx 2=0 … Fx 3=0

Optimización clásica condicionada A. Método de sustitución Optimizar f(x 1, x 2, x 3) sujeto a g 1(x 1, x 2, x 3)=0 x 1 =G(x 3) X 2=G(x 3) g 2(x 1, x 2, x 3)=0 Optimizar f( G(x 3), G(x 3) , x 3) Optimizar F(x 3) Optimización libre F(x 3) : Fx 3=0 …

Optimización clásica condicionada B. Multiplicadores de Lagrange Optimizar f(x 1, x 2 ) sujeto a g(x 1, x 2 )=0 F(x 1, x 2; )= f(x 1, x 2) - g(x 1, x 2) (1)

Optimización clásica condicionada B. Multiplicadores de Lagrange Optimizar f(x 1, x 2 ) sujeto a g(x 1, x 2 )=0 (1) F(x 1, x 2; )= f(x 1, x 2) - g(x 1, x 2) Fx 1=0 Fx 2=0 (a, b, 0) F =0 (a, b, 0) Mínimo relativo de F (a, b) es Mínimo relativo de (1) (a, b, 0) Máximo relativo de F (a, b) es Máximo relativo de (1) (a, b, 0) Punto silla o duda en F (a, b) es DUDA de (1)

Optimización clásica condicionada B. Multiplicadores de Lagrange Optimizar f(x 1, x 2, x 3) sujeto a g(x 1, x 2, x 3)=0 (1) F(x 1, x 2, x 3; )= f(x 1, x 2, x 3) - g(x 1, x 2, x 3) Fx 1=0 Fx 2=0 (a, b, c, 0) Fx 3=0 F =0 (a, b, c, 0) Mínimo relativo de F (a, b, c) es Mínimo relativo de (1) (a, b, c, 0) Máximo relativo de F (a, b, c) es Máximo relativo de (1) (a, b, c, 0) Punto silla o DUDA de F (a, b, c) es DUDA de (1)

Optimización clásica condicionada B. Multiplicadores de Lagrange Optimizar f(x 1, x 2 , x 3) sujeto a g 1(x 1, x 2, x 3)=0 (1) g 2(x 1, x 2, x 3)=0 F(x 1, x 2, x 3; 1, 2)= f(x 1, x 2, x 3) - 1 g 1(x 1, x 2, x 3) - 2 g 2(x 1, x 2, x 3) Fx 1=0 Fx 2=0 (a, b, c, 1, 2) Fx 3=0 F 1=0 F 2=0 (a, b, c, 1, 2 ) Mínimo relativo de F (a, b, c) es Mínimo relativo de (1)

Ejemplo comparativo Método de sustitución 2 2 2 (1) Opt. U = x + y + z s. a. 1+x+y-z=0 z=1+x+y (2) Opt. U = x 2 + y 2 + (1+x+y)2 Ux=2 x+2(1+x+y)=0 x=y=-1/3 Uy=2 y+2(1+x+y)=0 Uxx=2+2=4 Uyy=2+2=4 Uxy=2 (-1/3, -1/3) Mín. rel. (2) (-1/3, 1/3) Mín. rel. de (1) Multiplicadores de Lagrange F(x, y, z, )=x 2 + y 2 + z 2 - (x+y+1 -z) Fx=2 x+ =0 Fy=2 y+ =0 Fz=2 z- =0 F =x+y+1 -z=0 x=y=-z -3 z+1=0 z=1/3 A (-1/3, 1/3 ; -2/3) Punto crítico Fxx=2 Fyy=2 Fzz=2 Fxy=Fxz=Fyz =0

Ejemplo comparativo Método de sustitución 2 2 2 (1) Opt. U = x + y + z s. a. 1+x+y-z=0 z=1+x+y (2) Opt. U = x 2 + y 2 + (1+x+y)2 Ux=2 x+2(1+x+y)=0 x=y=-1/3 Uy=2 y+2(1+x+y)=0 Uxx=2+2=4 Uyy=2+2=4 Uxy=2 Multiplicadores de Lagrange F(x, y, z, )=x 2 + y 2 + z 2 - (x+y+1 -z) Fx=2 x+ =0 Fy=2 y+ =0 Fz=2 z- =0 F =x+y+1 -z=0 x=y=-z -3 z+1=0 z=1/3 A (-1/3, 1/3 ; -2/3) Punto crítico (-1/3, -1/3) Mín. rel. (2) (-1/3, 1/3) Mín. rel. de (1) (-1/3, 1/3 ; -2/3) Min rel. F (-1/3, 1/3 ) Min rel. (1)

Otra forma de estudiar los puntos críticos: Hessiano Orlado

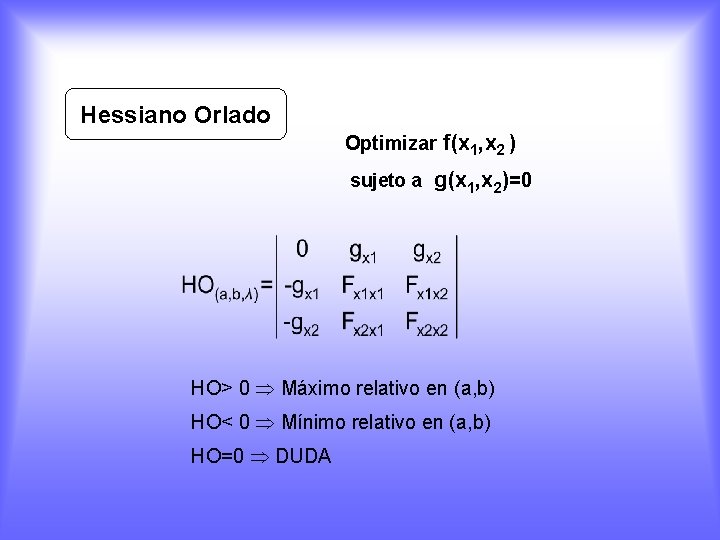
Hessiano Orlado Optimizar f(x 1, x 2 ) sujeto a g(x 1, x 2)=0 HO> 0 Máximo relativo en (a, b) HO< 0 Mínimo relativo en (a, b) HO=0 DUDA

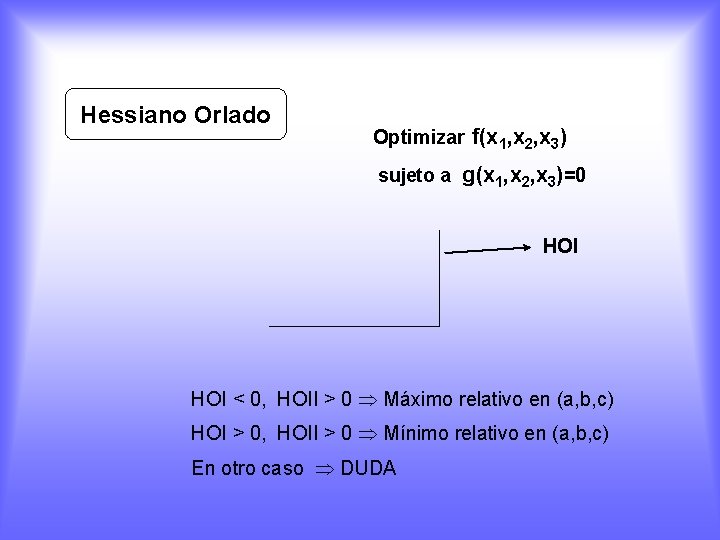
Hessiano Orlado Optimizar f(x 1, x 2, x 3) sujeto a g(x 1, x 2, x 3)=0 HOI < 0, HOII > 0 Máximo relativo en (a, b, c) HOI > 0, HOII > 0 Mínimo relativo en (a, b, c) En otro caso DUDA

Hessiano Orlado Optimizar f(x 1, x 2, x 3) sujeto a g(x 1, x 2, x 3 )=0 h(x 1, x 2, x 3)=0 HO <0 Máximo relativo en (a, b, c) HO >0 Mínimo relativo en (a, b, c) En otro caso DUDA