Lineare Optimierung von Dr Manfred GurtnerWrl 2020 Zuerst

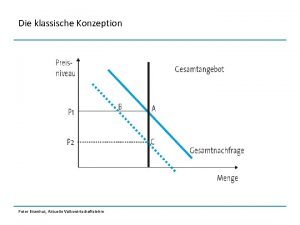
Lineare Optimierung von Dr. Manfred Gurtner−Würl 2020 Zuerst: Was ist Lineare Optimierung eigentlich? Wenn ich zum Beispiel im Gasthaus die Möglichkeit habe, einer Gruppe von Leuten Getränke um 60€ zu spendieren, wobei ein Seidel Bier 3€ kostet und ein Viertel Rotwein 4€ kostet. Dann frage ich mich, wie viel Bier und Wein kann ich bestellen, wenn ich höchstens 60€ ausgeben will.

Wenn ich genau 60€ ausgeben will, ergibt das die folgende Gleichung: 3€ pro Bier mal Anzahl der Biere plus 4€ pro Wein mal Anzahl der Weine ergibt 60 € Gesamtsumme: 3∙x+4∙y = 60 x sind die Anzahl an Seideln Bier, y sind die Anzahl an Vierteln Rotwein

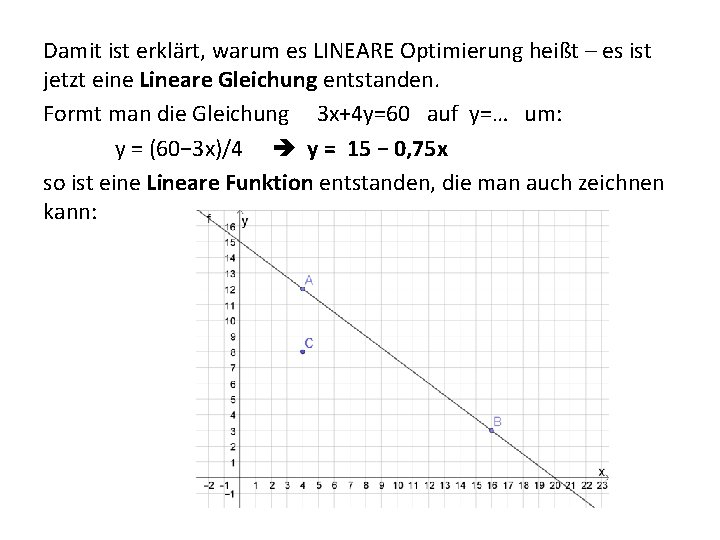
Damit ist erklärt, warum es LINEARE Optimierung heißt – es ist jetzt eine Lineare Gleichung entstanden. Formt man die Gleichung 3 x+4 y=60 auf y=… um: y = (60− 3 x)/4 y = 15 − 0, 75 x so ist eine Lineare Funktion entstanden, die man auch zeichnen kann:

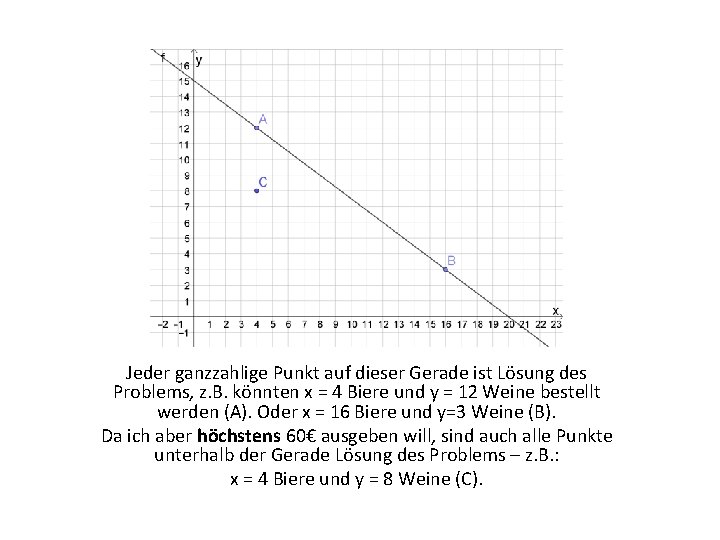
Jeder ganzzahlige Punkt auf dieser Gerade ist Lösung des Problems, z. B. könnten x = 4 Biere und y = 12 Weine bestellt werden (A). Oder x = 16 Biere und y=3 Weine (B). Da ich aber höchstens 60€ ausgeben will, sind auch alle Punkte unterhalb der Gerade Lösung des Problems – z. B. : x = 4 Biere und y = 8 Weine (C).

Wir wollen uns nun die folgende Maximierungsaufgabe genauer ansehen: Eine Jugendgruppe will Zelte einkaufen. In einem Sonderangebot werden zwei verschiedene Sorten von Zelten für jeweils 10 und 15 Personen preiswert angeboten. Von den 10 -Personenzelten sind nur noch 5 vorrätig Von den 15 -Personenzelten sind nur noch 4 vorrätig. Die Zelte für 10 Personen kosten 200 Euro je Stück Die Zelte für 15 Personen kosten 400 Euro je Stück. Die Jugendgruppe kann insgesamt höchstens 1800 Euro für die Zelte ausgeben. Wie viele 10 - und 15 -Personenzelte kann die Jugendgruppe kaufen, damit eine möglichst große Anzahl von Jugendlichen in den Zelten untergebracht werden kann?

Es ist nun möglich, alle diese Bedingungen in Lineare Funktionen umzuwandeln Das machen wir in 4 Schritten: 1. Schritt: Vom Text zu den Un/gleichungen 2. Schritt: Von den Un/gleichungen zu den Funktionen und zur Grafik 3. Schritt: Lösungspunkt grafisch mit der Zielfunktion bestimmen 4. Schritt: Lösung rechnerisch bestimmen (Zielpunkt und Zielfunktionswert) Dazu kann man sich das Video: https: //www. youtube. com/watch? v=vjfy 4 stuwk. A ansehen (die ersten 17 Minuten)

Jetzt wird das der Reihe nach durchgeführt: 1. Schritt: Vom Text zu den Un/gleichungen Dazu gehen wir von der Zielfunktionsfrage aus: Wie viele 10 - und 15 -Personenzelte kann die Jugendgruppe kaufen, damit eine möglichst große Anzahl von Jugendlichen in den Zelten untergebracht werden kann? Und bestimmen dazu die Variablen x und y: x ist die Anzahl der 10−Personenzelte y ist die Anzahl der 15−Personenzelte

1. Schritt: Vom Text zu den Un/gleichungen Jetzt werden die einzelnen Bedingungen in Ungleichungen übersetzt: Von den 10 -Personenzelten sind nur noch 5 vorrätig x≤ 5 Von den 15 -Personenzelten sind nur noch 4 vorrätig y≤ 4 Die Zelte für 10 Personen kosten 200 Euro je Stück Die Zelte für 15 Personen kosten 400 Euro je Stück Die Jugendgruppe kann insgesamt höchstens 1800 Euro für die Zelte ausgeben 200∙x + 400∙y ≤ 1800

2. Schritt: Von den Un/gleichungen zu den Funktionen Wir formen die Ungleichungen auf y um und können Sie dann zeichnen: x ≤ 5 kann so bleiben y ≤ 4 kann so bleiben 200∙x + 400∙y ≤ 1800 | 200 x wird subtrahiert 400 y ≤ 1800 − 200 x | : 400 y ≤ (1800 − 200 x)/400 y ≤ 4, 5 − 0, 5·x

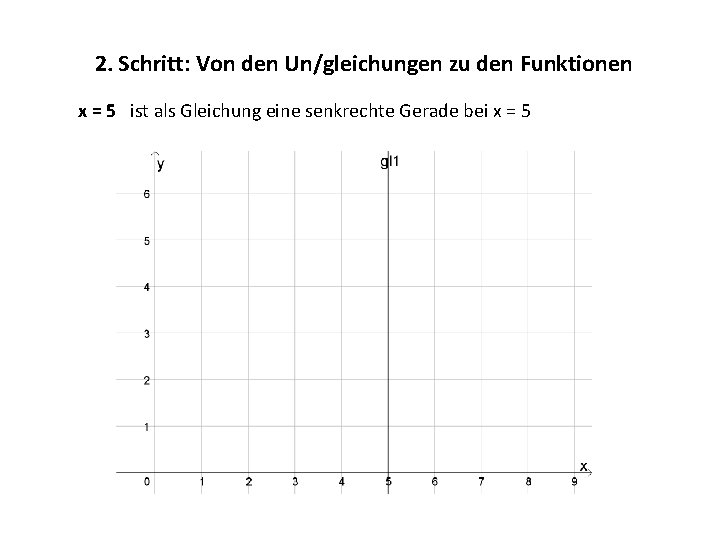
2. Schritt: Von den Un/gleichungen zu den Funktionen x = 5 ist als Gleichung eine senkrechte Gerade bei x = 5

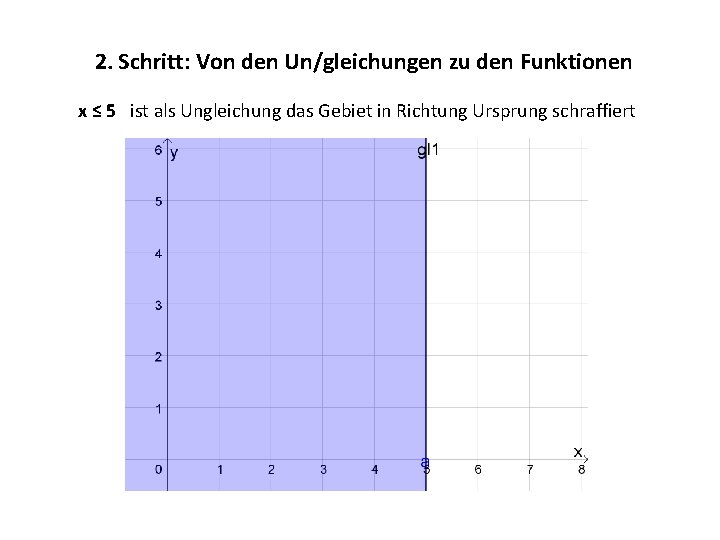
2. Schritt: Von den Un/gleichungen zu den Funktionen x ≤ 5 ist als Ungleichung das Gebiet in Richtung Ursprung schraffiert

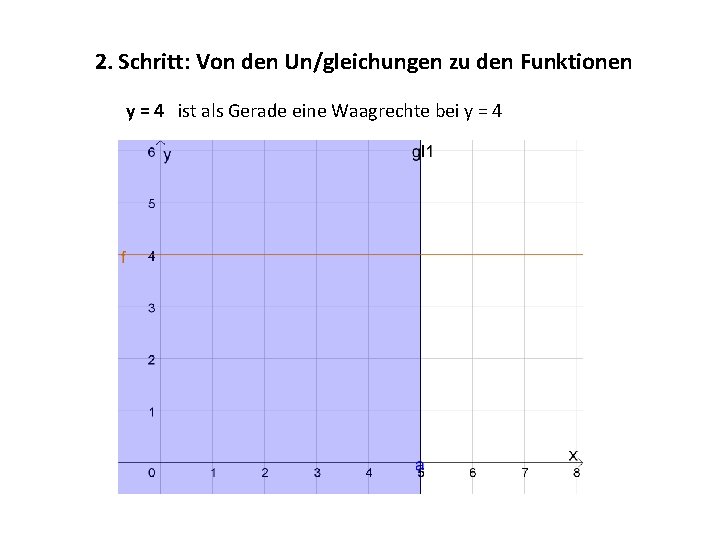
2. Schritt: Von den Un/gleichungen zu den Funktionen y = 4 ist als Gerade eine Waagrechte bei y = 4

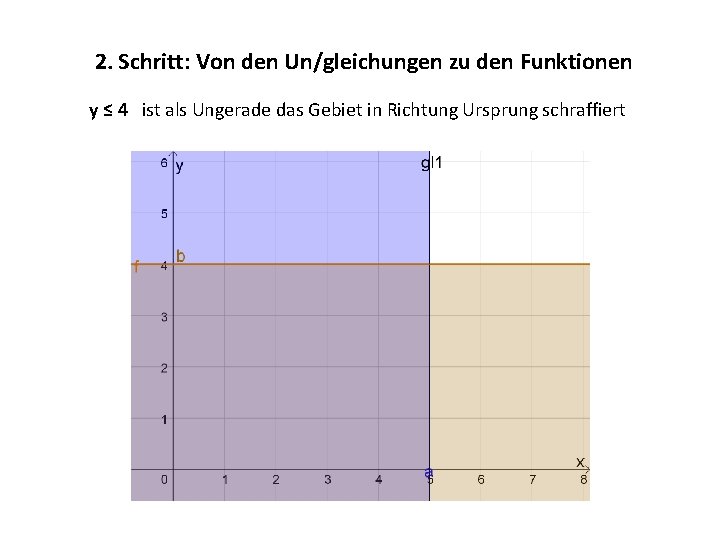
2. Schritt: Von den Un/gleichungen zu den Funktionen y ≤ 4 ist als Ungerade das Gebiet in Richtung Ursprung schraffiert

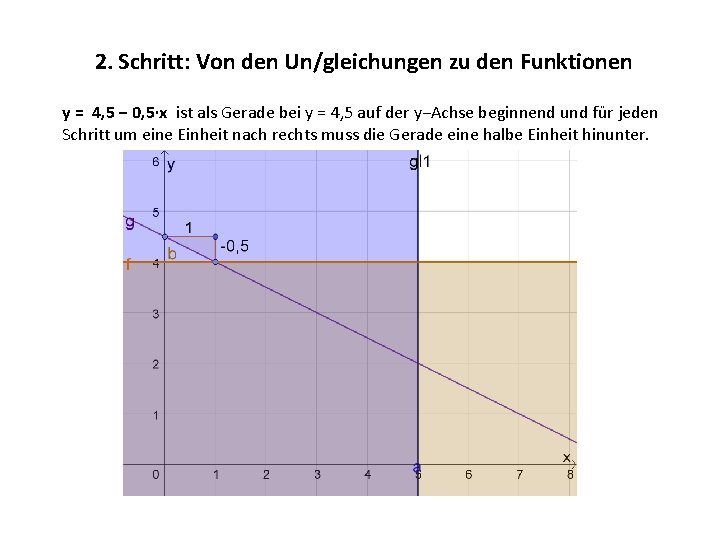
2. Schritt: Von den Un/gleichungen zu den Funktionen y = 4, 5 − 0, 5·x ist als Gerade bei y = 4, 5 auf der y−Achse beginnend und für jeden Schritt um eine Einheit nach rechts muss die Gerade eine halbe Einheit hinunter.

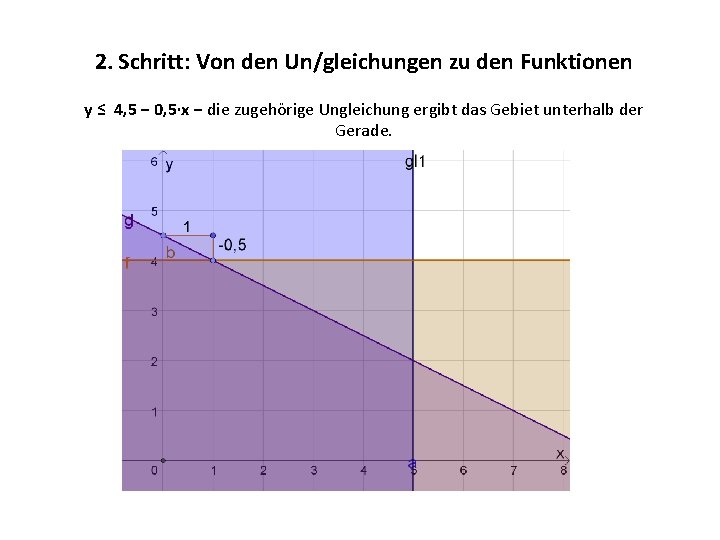
2. Schritt: Von den Un/gleichungen zu den Funktionen y ≤ 4, 5 − 0, 5·x − die zugehörige Ungleichung ergibt das Gebiet unterhalb der Gerade.

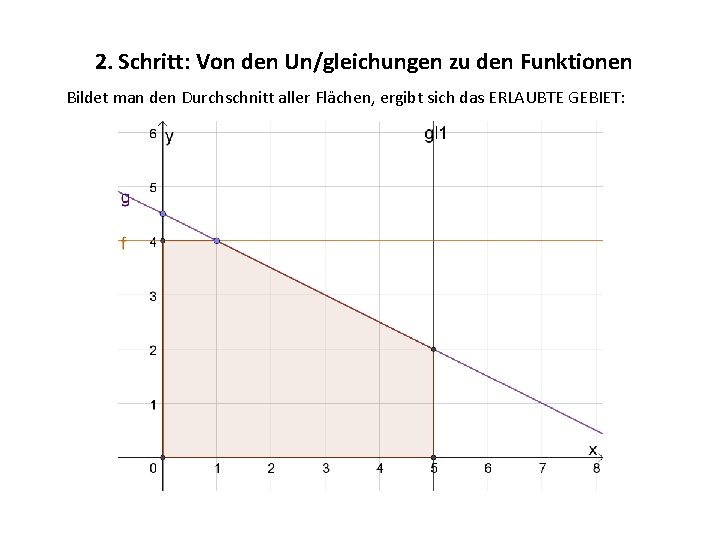
2. Schritt: Von den Un/gleichungen zu den Funktionen Bildet man den Durchschnitt aller Flächen, ergibt sich das ERLAUBTE GEBIET:

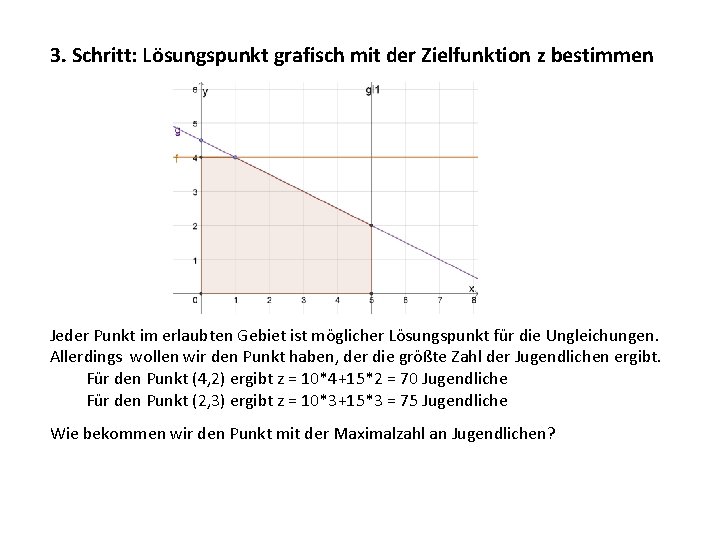
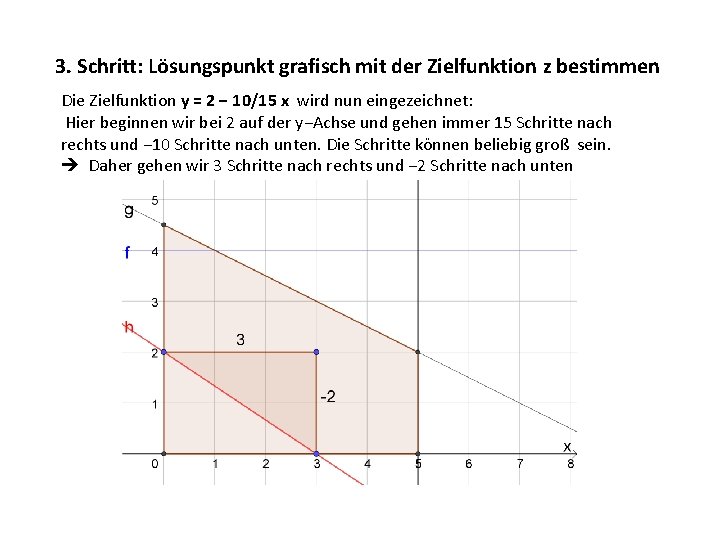
3. Schritt: Lösungspunkt grafisch mit der Zielfunktion z bestimmen Das Ziel ist: Wie viele 10 - und 15 -Personenzelte kann die Jugendgruppe kaufen, damit eine möglichst große Anzahl von Jugendlichen in den Zelten untergebracht werden kann? Die Anzahl der Jugendlichen ergibt sich aus: In den 10−Personenzelten sind 10 Jugendliche möglich, multipliziert mit den x Zelten, ergibt 10∙x Jugendliche In den 15−Personenzelten sind 15 Jugendliche möglich, multipliziert mit den y Zelten, ergibt 15∙y Jugendliche Beides zusammen ergibt die Zielfunktion z = 10 x+15 y Jugendliche

3. Schritt: Lösungspunkt grafisch mit der Zielfunktion z bestimmen Jeder Punkt im erlaubten Gebiet ist möglicher Lösungspunkt für die Ungleichungen. Allerdings wollen wir den Punkt haben, der die größte Zahl der Jugendlichen ergibt. Für den Punkt (4, 2) ergibt z = 10*4+15*2 = 70 Jugendliche Für den Punkt (2, 3) ergibt z = 10*3+15*3 = 75 Jugendliche Wie bekommen wir den Punkt mit der Maximalzahl an Jugendlichen?

3. Schritt: Lösungspunkt grafisch mit der Zielfunktion z bestimmen Die Zielfunktion z = 10 x+15 y müssen wir auch auf y = umformen: 10 x + 15 y = z | − 10 x 15 y = z− 10 x | : 15 y = z/15 − 10/15 x Um die Zielfunktion in die Zeichnung zu bekommen, setzen wir zuerst für z einen beliebigen Wert ein, sodass es einen praktischen Startwert auf der y−Achse ergibt. Hier z. B. : z = 30. Dann ergibt das : y = 2 − 10/15 x. Danach erhöhen wir z solange bis wir den optimalen Punkt erreichen − und das ergibt eine Parallelverschiebung der Gerade!

3. Schritt: Lösungspunkt grafisch mit der Zielfunktion z bestimmen Die Zielfunktion y = 2 − 10/15 x wird nun eingezeichnet: Hier beginnen wir bei 2 auf der y−Achse und gehen immer 15 Schritte nach rechts und − 10 Schritte nach unten. Die Schritte können beliebig groß sein. Daher gehen wir 3 Schritte nach rechts und − 2 Schritte nach unten

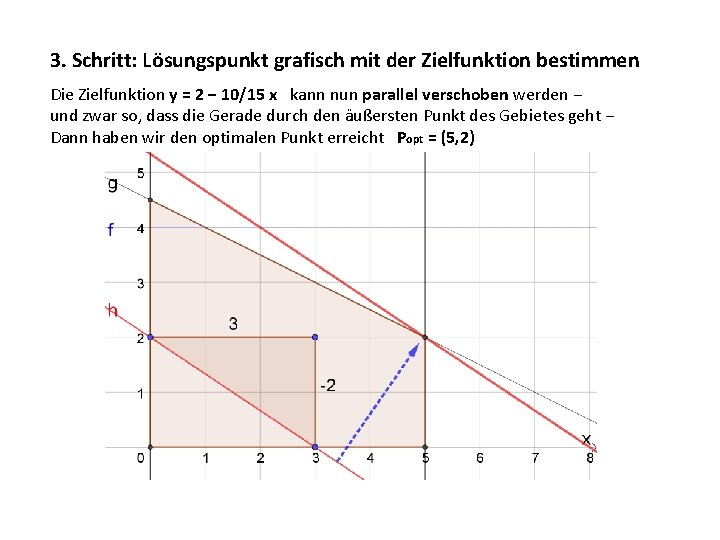
3. Schritt: Lösungspunkt grafisch mit der Zielfunktion bestimmen Die Zielfunktion y = 2 − 10/15 x kann nun parallel verschoben werden − und zwar so, dass die Gerade durch den äußersten Punkt des Gebietes geht − Dann haben wir den optimalen Punkt erreicht Popt = (5, 2)

4. Schritt: Lösung rechnerisch bestimmen (Zielpunkt und Zielfunktionswert) Der Schnittpunkt der beiden Geraden x = 5 und y = 4, 5 − 0, 5·x ergibt den Lösungspunkt. Das ist hier einfach − wir setzen x = 5 in die 2. Gleichung ein und erhalten: y = 4, 5 − 0, 5∙ 5 = 2 Damit erhalten wir die Lösung: Popt = (5, 2) Es müssen 5 Zelte mit 10 Personen und 2 Zelte mit 15 Personen gekauft werden. Das ergibt die Zielfunktionszahl z = 10*5 + 15*2 = 80 Personen

Das ist die Lösung: Es müssen 5 Zelte mit 10 Personen und 2 Zelte mit 15 Personen gekauft werden. Und es können 80 Jugendliche untergebracht werden. Da dies ein exakter Randpunkt des Gebietes ist, bleibt auch kein Geld übrig! FERTIG !