Linear momentum and Collisions Chapter 9 Center of

Linear momentum and Collisions Chapter 9

Center of mass and linear momentum I. The center of mass - System of particles / - Solid body II. Newton’s Second law for a system of particles III. Linear Momentum IV. - System of particles / Conservation V. IV. Collision and impulse VI. - Single collision / - Series of collisions V. Momentum and kinetic energy in collisions VI. Inelastic collisions in 1 D -Completely inelastic collision/

VII. Elastic collisions in 1 D VIII. Collisions in 2 D IX. Systems with varying mass X. External forces and internal energy changes

I. Center of mass The center of mass of a body or a system of bodies is the point that moves as though all the mass were concentrated there and all external forces were applied there.

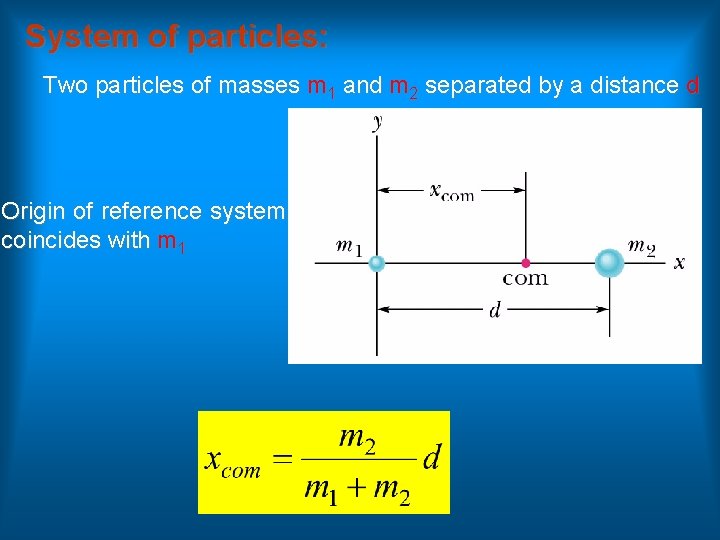
System of particles: Two particles of masses m 1 and m 2 separated by a distance d Origin of reference system coincides with m 1

System of particles: Choice of the reference origin is arbitrary Shift of the coordinate system but center of mass is still at the same distance from each particle. The center of mass lies somewhere between the two particles. General: M = total mass of the system

System of particles: We can extend this equation to a general situation for n particles that strung along x-axis. The total mass of the system M=m 1+m 2+m 3+……+mn The location of center of the mass: 3 D:

System of particles: 3 D: The vector form Position of the particle: Position COM M = mass of the object

Solid bodies: Continuous distribution of matter. Particles = dm (differential mass elements). 3 D: M = mass of the object Assumption: Uniform objects uniform density

The center of mass of an object with a point, line or plane of symmetry lies on that point, line or plane. The center of mass of an object does not need to lie within the object (Examples: doughnut, horseshoe )

Problem solving tactics: (1) Use object’s symmetry. (2) If possible, divide object in several parts. Treat each of these parts as a particle located at its own center of mass. (3) Chose your axes. Use one particle of the system as origin of your reference system or let the symmetry lines be your axis.

II. Newton’s second law for a system of particles Motion of the center of mass: Center of the mass of the system moves as a particle whose mass is equal to the total mass of the system. Fnet is the net of all external forces that act on the system. Internal forces (from one part of the system to another are not included). The system is closed: no mass enters or leaves the system during the movement. (M=total system mass). acom is the acceleration of the system’s center of mass.

Prove: (*) includes forces that the particles of the system exert on each other (internal forces) and forces exerted on the particles from outside the system (external). Newton’s third law internal forces from third-law force pairs cancel out in the sum (*) Only external forces.

III. Linear momentum The linear momentum of a particle is a vector p defined as: Momentum is a vector with magnitude equal mv and have direction of v. SI unit of the momentum is kg-meter/second

Newton II law in terms of momentum: The time rate of change of the momentum of a particle is equal to the net force acting on the particle and is in the direction of the force.

System of particles: The total linear moment P is the vector sum of the individual particle’s linear momentum. The linear momentum of a system of particles is equal to the product of the total mass M of the system and the velocity of the center of mass. Net external force acting on the system.

Conservation: If no external force acts on a closed, isolated system of particles, the total linear momentum P of the system cannot change. Closed: no matter passes through the system boundary in any direction.

Conservation of Linear Momentum If no net external force acts on the system of particles the total linear momentum P of the system cannot change. Each component of the linear momentum is conserved separately if the corresponding component of the net external force is zero. If the component of the net external force on a closed system is zero along an axis component of the linear momentum along that axis cannot change. The momentum is constant if no external forces act on a closed particle system. internal forces can change the linear momentum of portions of the system, but they cannot change the total linear momentum of the entire system.

IV. Collision and impulse Collision: isolated event in which two or more bodies exert relatively strong forces on each other for a relatively short time. Impulse: Measures the strength and duration of the collision force Third law force pair FR = - F L Single collision

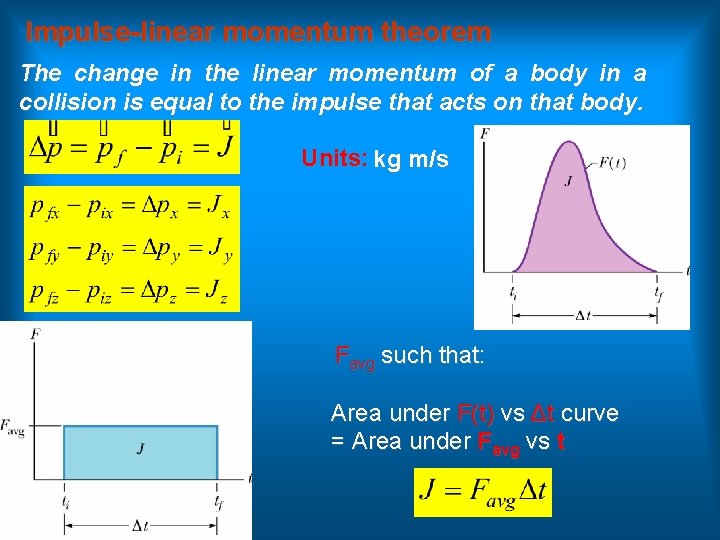
Impulse-linear momentum theorem The change in the linear momentum of a body in a collision is equal to the impulse that acts on that body. Units: kg m/s Favg such that: Area under F(t) vs Δt curve = Area under Favg vs t

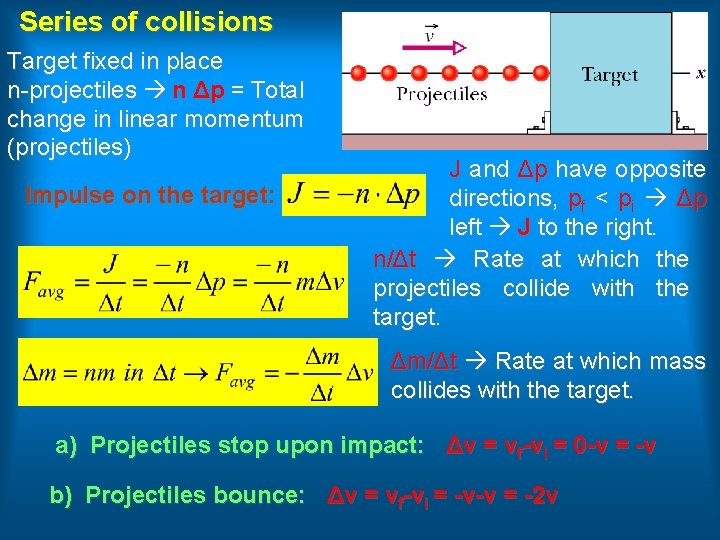
Series of collisions Target fixed in place n-projectiles n Δp = Total change in linear momentum (projectiles) Impulse on the target: J and Δp have opposite directions, pf < pi Δp left J to the right. n/Δt Rate at which the projectiles collide with the target. Δm/Δt Rate at which mass collides with the target. a) Projectiles stop upon impact: Δv = vf-vi = 0 -v = -v b) Projectiles bounce: Δv = vf-vi = -v-v = -2 v

V. Momentum and kinetic energy in collisions Assumptions: Closed systems (no mass enters or leaves them) Isolated systems (no external forces act on the bodies within the system) Elastic collision: If the total kinetic energy of the system of two colliding bodies is unchanged (conserved) by the collision. Inelastic collision: The kinetic energy of the system is not conserved some goes into thermal energy, sound, etc. Completely inelastic collision: After the collision the bodies lose energy and stick together.

Velocity of the center of mass: In a closed, isolated system, the velocity of COM of the system cannot be changed by a collision. (No net external force). Completely inelastic collision v = vcom

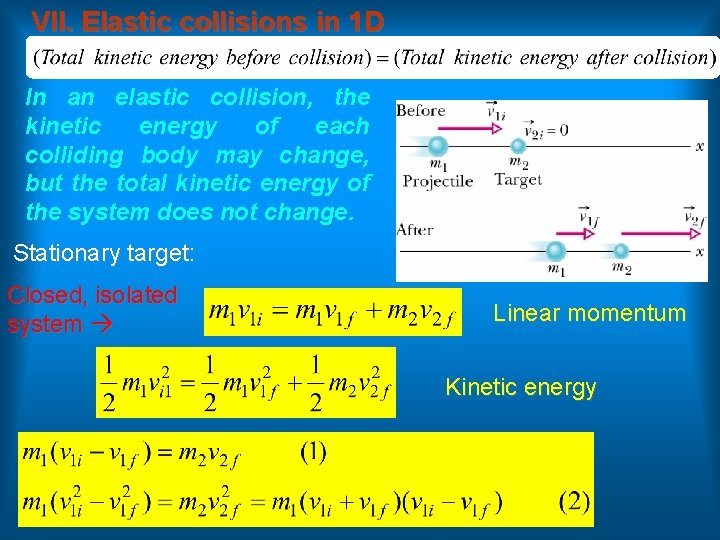
VII. Elastic collisions in 1 D In an elastic collision, the kinetic energy of each colliding body may change, but the total kinetic energy of the system does not change. Stationary target: Closed, isolated system Linear momentum Kinetic energy

Stationary target: v 2 f >0 always v 1 f >0 if m 1>m 2 forward mov. v 1 f <0 if m 1<m 2 bounce back Equal masses: m 1=m 2 v 1 f=0 and v 2 f = v 1 i In head-on collisions bodies of equal masses simply exchange velocities.

Massive target: m 2>>m 1 v 1 f ≈ -v 1 i and v 2 f ≈ (2 m 1/m 2)v 1 i Body 1 bounces back with approximately same speed. Body 2 moves forward at low speed. Massive projectile: m 1>>m 2 v 1 f ≈ v 1 i and v 2 f ≈ 2 v 1 i Body 1 keeps on going barely lowed by the collision. Body 2 charges ahead at twice the initial speed of the projectile.

VII. Elastic collisions in 1 D Moving target: Closed, isolated system Linear momentum Kinetic energy

VIII. Collisions in 2 D Closed, isolated system Linear momentum conserved Elastic collision Kinetic energy conserved Example: If the collision is elastic

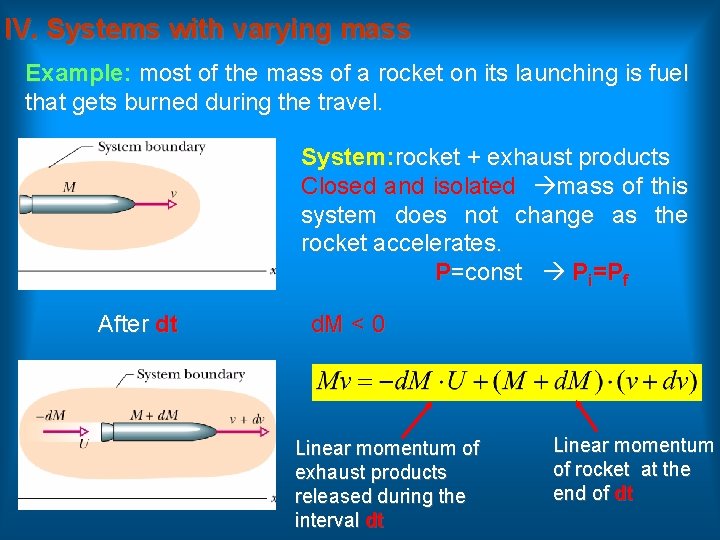
IV. Systems with varying mass Example: most of the mass of a rocket on its launching is fuel that gets burned during the travel. System: rocket + exhaust products Closed and isolated mass of this system does not change as the rocket accelerates. P=const Pi=Pf After dt d. M < 0 Linear momentum of exhaust products released during the interval dt Linear momentum of rocket at the end of dt

Velocity of rocket relative to frame = (velocity of rocket relative to products)+ (velocity of products relative to frame) R=Rate at which the rocket losses mass= -d. M/dt = rate of fuel consumption First rocket equation

Second rocket equation

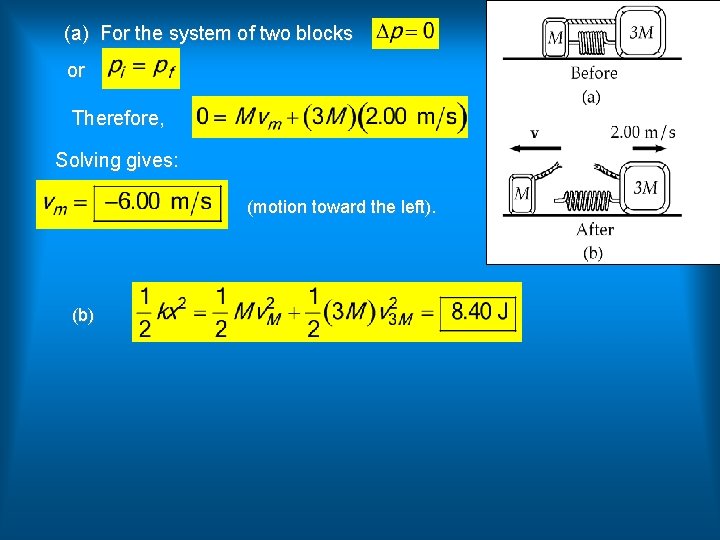
Two blocks of masses M and 3 M are placed on a horizontal, frictionless surface. A light spring is attached to one of them, and the blocks are pushed together with the spring between them. A cord initially holding the blocks together is burned; after this, the block of mass 3 M moves to the right with a speed of 2. 00 m/s. (a) What is the speed of the block of mass M? (b) Find the original elastic potential energy in the spring if M = 0. 350 kg.

(a) For the system of two blocks or Therefore, Solving gives: (motion toward the left). (b)

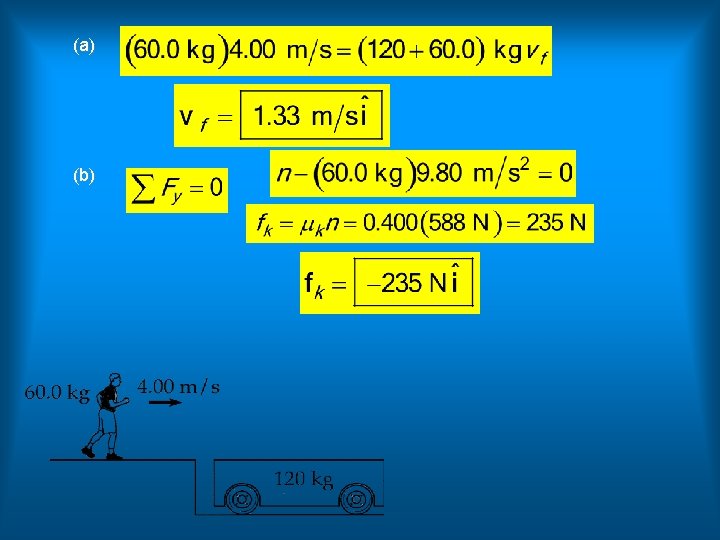
A 60. 0 -kg person running at an initial speed of 4. 00 m/s jumps onto a 120 -kg cart initially at rest (Figure P 9. 55). The person slides on the cart’s top surface and finally comes to rest relative to the cart. The coefficient of kinetic friction between the person and the cart is 0. 400. Friction between the cart and ground can be neglected. (a) Find the final velocity of the person and cart relative to the ground. (b) Find the friction force acting on the person while he is sliding across the top surface of the cart. (c) How long does the friction force act on the person? (d) Find the change in momentum of the person and the change in momentum of the cart. (e) Determine the displacement of the person relative to the ground while he is sliding on the cart. (f) Determine the displacement of the cart relative to the ground while the person is sliding. (g) Find the change in kinetic energy of the person. (h) Find the change in kinetic energy of the cart. (i) Explain why the answers to (g) and (h) differ. (What kind of collision is this, and what accounts for the loss of mechanical energy? )

(c) For the person, (d) person: (e) (f) cart:

(g) (h) (i) The force exerted by the person on the cart must equal in magnitude and opposite in direction to the force exerted by the cart on the person. The changes in momentum of the two objects must be equal in magnitude and must add to zero. Their changes in kinetic energy are different in magnitude and do not add to zero. The following represent two ways of thinking about “way”. The distance the cart moves is different from the distance moved by the point of applicatio 9 n of the friction force to the cart. The total change of mechanical energy for both objects together, -320 J, becomes +320 J of additional internal energy in this perfectly inelastic collision.